§ 2. Контрольные вопросы и задания

1. Сформулируйте определения полуторалинейной и билинейной форм.

2. Что такое матрица полуторалинейной формы в данном базисе Изложите метод, которым можно построить такую матрицу.

3. Какая полуторалинейная форма называется эрмитовой

4. Известно, что матрица полуторалинейной формы эрмитова в некотором базисе. Будет ли она эрмитовой в любом другом базисе

5. Укажите две различные билинейные формы, из которых получается следующая квадратичная форма B(x,x)=  x₁² + 5x₁x₂  x₁x₃ + 2x₂x₃ + x₂². Какая билинейная форма будет полярной к заданной квадратичной форме?

6. Для каких полуторалинейных форм вводится понятие канонического вида и канонического базиса

7. Какие две квадратичные формы можно одновременно привести к каноническому виду невырожденным преобразованием

8. Изложите метод одновременного приведения пары квадратичных форм к каноническому виду.

§ 3. Примеры решения задач

1. Составить матрицу полуторалинейной формы

B(x,y) = .

Является ли данная полуторалинейная форма эрмитовой

Решение. Вспомним, что матрица В с матричными элементами b_ij = B(e_i, e_j) называется матрицей полуторалинейной формы и .

Поэтому, для составления матрицы билинейной формы, элементы b_ij положим равными коэффициентам при . В результате получим матрицуВ = . Т. к. элементы матрицы формы не связаны соотношением, то форма не является эрмитовой.

2. Привести квадратичную форму

B(x,x) = 3x₂² + 3x₃² + 4x₁x₂+ 4x₁x₃– 2x₂x₃

к каноническому виду. Найти канонический базис и матрицу перехода

в этот базис.

Решение. Составим матрицу квадратичной формы

В =

и характеристическое уравнение для присоединенного оператора

   = = = 0.

Характеристическое уравнение имеет корни _1,2 = 4 и ₃ = 2. Эти корни являются собственными значениями линейного оператора, присоединенного к квадратичной форме. Найдем соответствующие им собственные векторы. Подставляя в матричное уравнение (B – E) X = 0, вместо , собственное значение  = 4 и решая получившуюся систему линейных уравнений, находим два линейно независимых собственных вектора, соответствующих собственному значению 4.

e₁ = ( 1, 2, 0) , e₂ = ( 1, 0, 2).

Аналогично находим собственный вектор, соответствующий собственному значению  = 2. Это вектор e₃ = ( 2, –1, –1).

Три найденных вектора образуют в пространстве собственный базис линейного оператора.

Следует помнить, что когда мы говорим о собственном базисе линейного оператора, мы имеем в виду базис пространства, состоящий из собственных векторов этого оператора.

Записывая координаты собственных векторов в столбцы матрицы, получим матрицу перехода из исходного базиса в новый базис.

P=.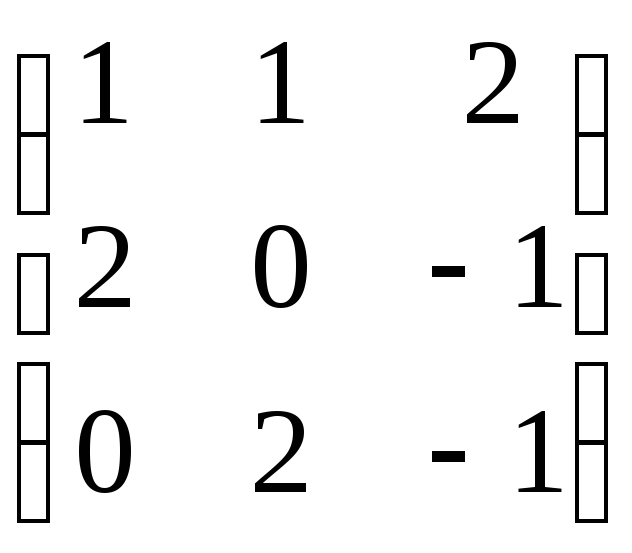

Используем формулы преобразования матрицы линейного оператора и матрицы квадратичной формы при изменении базиса. Обратим внимание на то, что

,

т. е. матрица линейного оператора действительно приводится к диагональному виду. Однако

.

Полученный результат свидетельствует о том, что матрица билинейной формы в новом базисе не имеет диагонального вида, т. е. найденный базис не является каноническим базисом квадратичной формы.

В чем же делоДля ответа на этот вопрос, перейдем к следующей задаче.

3.Построить матрицу ортогонального преобразования, приводящего квадратичную формуB(x,x) = 3x₂² + 3x₃² + 4x₁x₂+ 4x₁x₃– 2x₂x₃к каноническому виду.

Решение. При решении предыдущей задачи установлено, что векторы e₁ = ( 1, 2, 0), e₂ = ( 1, 0, 2), e₃ = ( 2, -1, -1) образуют собственный базис линейного оператора, присоединенного к матрице квадратичной формы, причем первые два отвечают одному и тому же собственному значению.

Вектор e₃ ортогонален векторам e₁ и e₂, которые, однако, не ортогональны друг другу. Т. е. полученный базис не ортогонален. Чтобы получить ортогональный базис, выполним процесс ортогонализации векторов e₁ и e₂. Это возможно проделать, поскольку оба вектора отвечают одному и тому же собственному значению.

Вектор f₁ нового базиса положим равным e₁, а вектор f₂ будем искать, как линейную комбинацию векторов e₂ и f₁ f₂ = e₂+ f₁ . Коэффициент  находится из условия ортогональности векторов f₁ и f₂ . Он равен (–0,2) и, таким образом, положив f₃ = e_{3 ,} получаем ортогональный базис из собственных векторов:

f₁ = (1, 2, 0) , f₂ = (4/5, –2/5, 2), f₃ = (1, 0, 2).

Если нормировать эти векторы, и записать их координаты в столбцы матрицы, мы получим матрицу ортогонального преобразования, приводящего исходную квадратичную форму к каноническому виду.

P = .

Прежде всего, отметим, что матрица перехода ортогональна, т. е. Р^Т = Р^–1и тогда . Следовательно

Последнее равенство показывает, что в данном базисе линейный оператор имеет диагональный вид, а квадратичная форма имеет канонический вид.

Это и неудивительно, ибо матрица перехода ортогональна и в новом базисе матрица линейного оператора и матрица квадратичной формы совпадают.

По сути, это и есть ответ на вопрос предыдущей задачи. Будьте осторожны  только в случае ортогонального преобразования матрица линейного оператора и матрица квадратичной формы преобразуются одинаково.

Если же необходимо найти канонический вид и канонический базис квадратичной формы с помощью преобразования, которое не обязательно является ортогональным, то можно воспользоваться одним из ранее изученных методов, например, методом Лагранжа или методом Якоби.

4. Квадратичная форма в некотором базисе имеет вид

B(x,x) = 2x₁² + 5x₂² + 4x₁x₂.

Задана также матрица Грамма того же базисаГ =. Найти операторАтакой, чтоB(x,y) = (x,Ay).

Решение. Прежде всего напомним, как связаны между собой в не ортонормированном базисе матрица полуторалинейной формыи матрицы линейных операторовив представлении:

,

.

Также отметим два факта, которые будут весьма полезными для решения данной задачи

а) в неортогональном базисе с известной матрицей Грамма скалярное произведение векторов может быть вычислено по формуле (x,y) = (x, Гy), где скалярное произведение в правой части находится по правилам, справедливым в ортонормированном базисе.

б) в соотношении B(x,y) = (x,Ay) матрица оператораАсовпадает с матрицей билинейной формыВ.

Тогда исходное соотношение можно записать в виде B(x,y) = (x, ГAy). Следовательно,В= ГAи, значит,A = Г^-1В .

Запишем матрицу квадратичной формы: В = . Матрица, обратная к матрице Грамма легко находится уже известными нам методами и равна Г^-1= . Теперь легко найти матрицу искомого оператораА.

A = Г^-1В = =.

5.Привести пару квадратичных формА(x,x) иB(x,x) к каноническому виду, если

А(x,x) =x₁²+ 17x₂²+ 3x₃²+ 4x₁x₂– 2x₁x₃– 14x₂x₃,

B(x,x) = x₁² – 15x₂² + 4x₁x₂ – 2x₁x₃ + 6x₂x₃ .

Указать базис, в котором пара форм имеет канонический вид.

Решение. Прежде всего, запишем матрицы заданных квадратичных форм А=В =. Вычисляя главные миноры этих матриц, устанавливаем, что у матрицыАони все положительны, т. е. квадратичная формаА(x,x) положительно определена и, следовательно, характеристическое уравнение имеет вид

 А  = .

Раскрывая определитель, получим характеристическое уравнение в виде

(1 ) (3) (2) = 0,

корнями которого, очевидно, являются числа ₁=3,₂=1,₃=2.

Теперь, решая матричное уравнение (B-А)X= 0 для каждого из полученных, находим соответствующие собственные векторы. В результате получим

₁=3e₁= ( 0, 1, 2)₂=1e₂= ( 1, 0, 0)₃=2e₃= ( 1, 1, 3) .

Если в качестве скалярного произведения рассматривать билинейную форму А(x,y) =x₁²+ 17x₂²+ 3x₃²+ 4x₁x₂– 2x₁x₃– 14x₂x₃, то нетрудно убедиться в том, что система векторов {e₁,e₂,e₃} является ортонормированной.

Записывая координаты найденных векторов в столбцы матрицы, получаем матрицу перехода из исходного, стандартного базиса в базис {e₁,e₂,e₃}

.

Если мы посмотрим, как изменятся матрицы исходных квадратичных форм при переходе в новый базис, то обнаружим, что

,

.

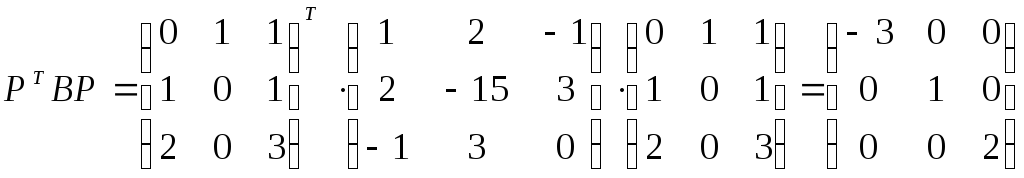Поскольку матрица Ав новом базисе является единичной, а матрицаВ– диагональной, то квадратичная формаA(x,x) в новом базисе имеет нормальный вид (коэффициенты квадратичной формы в каноническом базисе равны по модулю 1), а формаB(x,x) – канонический вид.

Итак, в базисе { e₁( 0, 1, 2),e₂( 1, 0, 0),e₃( 1, 1, 3) } формы имеют следующий вид

А(x,x) =x₁²+x₂²+x₃²,B(x,x) = –3x₁²+x₂²+ 2x₃².