§ 4. Задачи и упражнения для самостоятельной работы

1. Составить матрицы данных полуторалинейных форм в n-мерном унитарном пространстве:

а) – ix₁(n = 1); б) –ix₁(n = 2);

в) 3х₁+ 4ix₁– 5x₂+ ix₂(n = 2);

г) – 3iх₁+ 2x₁+ 2x₂+ (1 –i)x₂(n = 2);

 а) (– i); б); в); г). ▲

2. Составить матрицы данных полуторалинейных форм в n-мерном унитарном пространстве:

а) (1 + i)х₁+ (1 +i) x₂– 5x₂ (n = 2);

б) (1 + i) х₁+ (1  i) x₂– 5x₂ (n = 2);

в) х₁– 3x₂+ (2 + i) x₃– ix₁+ (4 + i) x₃ (n = 3).

 а) ; б); в). ▲

3. Записать эрмитову квадратичную форму с заданной матрицей:

а) ; б); в);

г) .

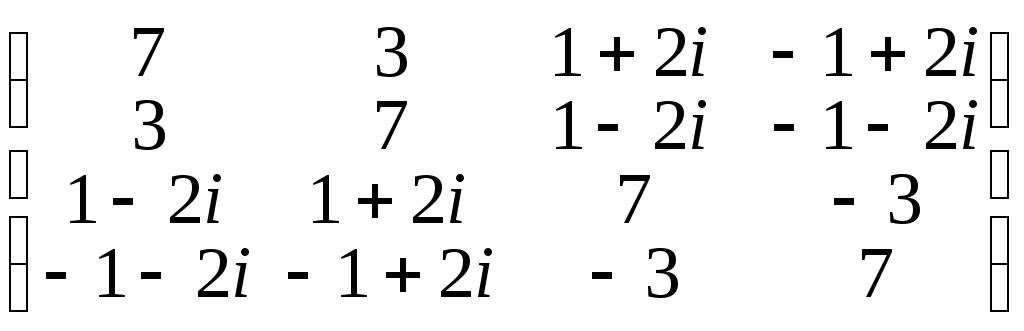 а) 5|x₁|²– 2х₁– 2х₂+ 8|x₂|²; б) е^i2/3(x₁+х₂); в) 8|x₂|²+ 2х₁+ 2х₂+х₁+

+ х₃+ 2х₂+2х₃; г) 7(|x₁|²+ |x₂|² +|x₃|²+ |x₄|²) +3х₁+ 3х₂+ (1 + 2i)х₁+

+ (1 – 2i)х₃+ (–1 + 2i)х₁– (1 + 2i)х₄+ (1 – 2i)х₂+ (1 + 2i)х₃– (1 + 2i)х₂+

+ (–1 + 2i)х₄– 3х₃– 3х₄. ▲

4. В n-мерном линейном пространствеV_nдана полуторалинейная форма. Показать, что значения соответствующей квадратичной формывещественны. ЕслиА(х,х) положительно определена, то скалярное произведение вV_nможет быть определено формулой: (х,у) =А(х,у).

5. Квадратичная (билинейная) форма записана в ортонормированном базисе двухмерного евклидового пространства. Записать канонический вид формы и матрицу Рперехода в базис, в котором матрица формы имеет диагональный вид:

а) ; б); в);

г) ; д).

 а) ;; б);; в);

; г);; д);.▲

6. Квадратичная (билинейная) форма записана в ортонормированном базисе трехмерного евклидового пространства. Записать канонический вид формы и матрицу Рперехода в базис, в котором матрица формы имеет диагональный вид:

а) ;

б) x₁y₁–х₁у₂–х₂у₁– 2х₂у₂–х₂у₃–х₃у₂+х₃у₃;

в) 2x₁y₂+ 2х₂у₁– 2х₁у₃– 2х₃у₁+ 4х₂у₂+ 4х₂у₃+ 4х₃у₂– 3х₃у₃;

 а) ;; б);;

в);. ▲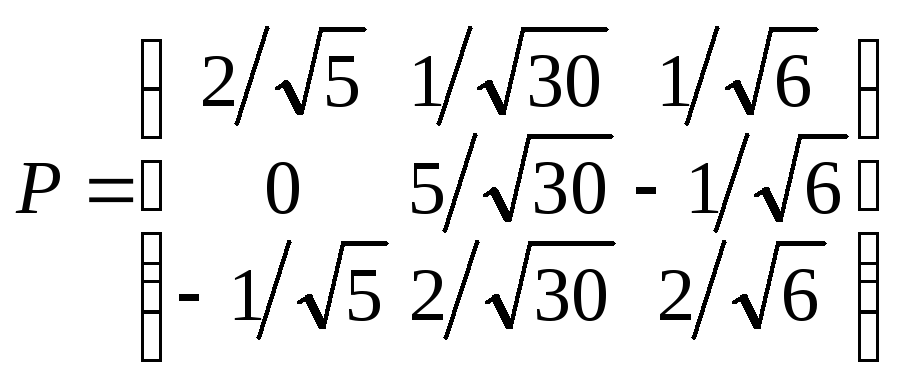

7. Квадратичная (билинейная) форма записана в ортонормированном базисе трехмерного евклидового пространства. Записать канонический вид формы и матрицу Рперехода в базис, в котором матрица формы имеет диагональный вид:

а) ;

б) x₁y₂+х₂у₁– 2х₁у₃– 2х₃у₁–х₁у₁–х₂у₂+ 2х₂у₃+ 2х₃у₂– 4х₃у₃;

в) x₁y₂+х₂у₁+х₁у₃+х₃у₁+х₂у₂–х₃у₃.

 а) ;; б);;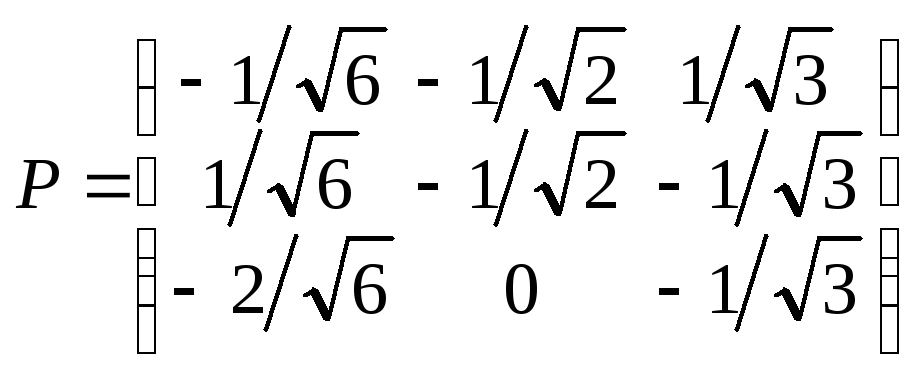

в) ;. ▲

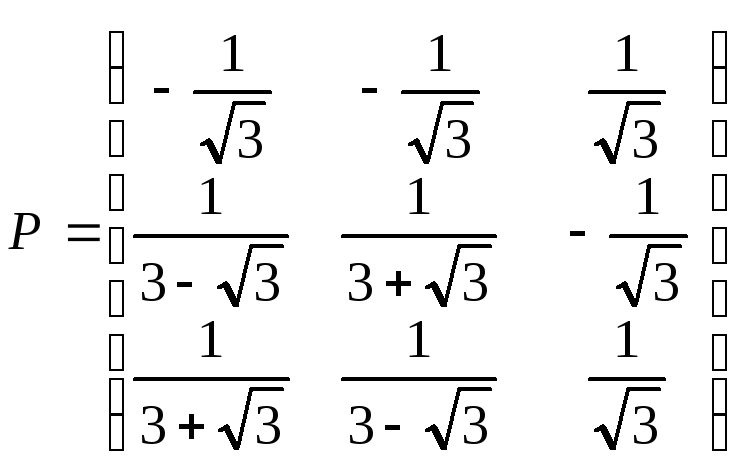8. Найти ортогональное преобразование, приводящее следующие квадратичные формы к каноническому виду, и записать этот канонический вид (преобразование определено не однозначно).

а) ; б);

в) ;

• а) ;;;;

б) ;;;;

в) ;;;

;. ▲

9. Найти ортогональное преобразование, приводящее следующие квадратичные формы к каноническому виду, и написать этот канонический вид (преобразование определено не однозначно).

а) ;

б) ; в).

Δа);;;;

б) ;;;; в);;;;. ▲

10. Квадратичная форма В(х,х) задана в базисе {e_i}, для которого матрица Грамма – Г также задана. Найти матрицу оператораАтакого, что

В(х,у) = (х,Ау):

а) ,; б),;

в) ,;

 а) ; б); в). ▲

10. Квадратичная форма В(х,х) задана в базисе {e_i}, для которого матрица Грамма – Г, также задана. Найти матрицу оператораАтакого, что

В(х,у) = (х,Ау):

а) ,;

б) ,;

в) ,.

 а) ; б) 3; в). ▲

12. Если от одной квадратичной формы можно перейти к другой посредством ортогонального преобразования, то две такие квадратичные формы называются ортогонально эквивалентными. Доказать, что для ортогональной эквивалентности необходимо и достаточно, чтобы характеристические многочлены их матриц совпадали.

13. Какие из следующих квадратичных форм ортогонально эквивалентны:

а) ,

,

;

б) ,

,

.

 а) А(х,х) иB(y,y); б)А(y,y) иC(z,z). ▲

14. Можно ли следующие пары квадратичных форм в вещественном пространстве привести одновременно к каноническому виду:

а) ,;

б) ,+ 3;

в) ,.

 а) нельзя; б) можно; в) нельзя . ▲

15. Привести одновременно к каноническому виду формы А(х,х) иВ(х,х) > 0:

а) ,

;

б) ,

;

в) ,

.

 а) А(х,х) =,В(х,х) =; б)А(х,х) =,

В(х,х) =; в)А(х,х) =,В(х,х) =. ▲

16. Не находя замены координат, приводящей положительно определенную форму gк нормальному виду, а формуf– к каноническому, найти этот канонический вид формыf:

а) ,;

б) ,;

в) ,;

г) ,.

 а) ; б); в); г). ▲

17. Найти преобразование координат, одновременно приводящее одну из двух данных квадратичных форм к нормальному виду, а другую к каноническому виду и записать этот вид:

а) ,;

б) ,;

в) ,;

г) ,;

 а) А(х,х) =,В(х,х) =,,;

б) А(х,х) =,В(х,х) =,,;

в) А(х,х) =,В(х,х) =,,;

г) А(х,х) =,В(х,х) =,,или

А(х,х) =,В(х,х) =,,. ▲

18. Найти преобразование координат, одновременно приводящее одну из двух данных квадратичных форм к нормальному виду, а другую – к каноническому виду, и записать этот вид:

а) ,;

б) ,;

в) ,;

г) ,

.

 а) А(х,х) =,В(х,х) =,,;

б) А(х,х) =,В(х,х) =,,;

в) А(х,х) =,В(х,х) =,,;

или А(х,х) =,В(х,х) =,,;

г) А(х,х) =,В(х,х) =,,;

. ▲

19. Найти ортогональное преобразование, приводящее следующие квадратичные формы к каноническому виду (приведение к главным осям), и написать этот канонический базис:

а) ;

б) ;

в) ;

г) .

• а) ;;;;

б) ;;;;

в) ;;;;

г) ;;;. ▲

20. Найти ортогональное преобразование, приводящее следующие квадратичные формы к каноническому виду (приведение к главным осям), и написать этот канонический базис:

а) ;

б) ;

в) ;

г) .

• а) ;;;;

б) ;;;

;; в);;

;;; г);;

;;. ▲