
Adaptatsionny_Kurs_Kulik
.pdf
k,
k
Учитывая периодичность тангенса, перенесѐм параллельно график вдоль оси
Z .
Ox
на
График функции y tg x называется тангенсоидой. |
|
|
|
|
|
|||
IV. График функции |
y ctg x . |
|
|
|
|
|
|
|
|
|
|
y ctg x получим из графика функции |
|||||
Так как ctg x tg x |
, то график функции |
|||||||
|
|
2 |
|
|
|
|
|
|
y tg x |
его параллельным |
переносом вдоль оси |
Ox |
на |
|
|
|
и симметричным |
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
отображением полученного графика относительно оси |
Ox : |
|
|
|
|
|
||
График функции y ctg x называется котангенсоидой.
82

5. Соотношения между тригонометрическими фукнкциями одного аргумента
Для единичной окружности: sin y ; |
cos x . Но |
y |
2 |
x |
2 |
1. |
|
|
|||||||||||
|
|
|
|
||||||||||||||||
Отсюда: sin |
2 |
cos |
2 |
1 |
– основное тригонометрическое тождество. |
||||||||||||||
|
|
||||||||||||||||||
tg sin , |
ctg |
cos |
|
ctg |
1 |
|
|
tg ctg 1 . |
|
|
|||||||||
sin |
tg |
|
|
|
|||||||||||||||
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Разделим последовательно |
равенство |
sin |
2 |
cos |
2 |
1 |
на cos |
2 |
0 |
||||||||||
|
|
|
|||||||||||||||||
получим:
и
sin |
2 |
|
|
0
,
|
1 tg2 |
|
1 |
|
|
; |
|
1 ctg2 |
|
1 |
|
|
. |
|
|
|
|
|
|
|
|||||||
|
cos2 |
|
sin2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
По этим формулам |
можно найти значения всех тригонометрических функций по |
||||||||||||
заданному значению одной функции.
6. Формулы тригонометрических функций суммы и разности двух чисел
Синус суммы: |
sin sin cos cos sin |
|||||
синус разности: |
sin sin cos cos sin |
|||||
косинус суммы: |
cos cos cos sin sin |
|||||
косинус разности: |
cos cos cos sin sin |
|||||
тангенс суммы: |
tg |
tg tg |
; |
|||
1 |
tg tg |
|||||
|
|
|
|
|||
тангенс разности: |
tg |
tg tg |
. |
|||
1 |
tg tg |
|||||
|
|
|
|
|||
;
;
;
;
7. Формулы двойного аргумента
cos 2
|
|
sin 2 2sin cos |
|||||
cos |
2 |
sin |
2 |
1 2sin |
|||
|
|
||||||
|
|
tg 2 |
2 tg |
||||
|
|
1 tg |
2 |
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|
||
; |
|
2 |
|
|
|
.
2cos |
2 |
|
1
;
8.Формулы преобразования суммы и разности тригонометрических функций
впроизведение и наоборот
Формулы суммы и разности одноимѐнных тригонометрических функций:
sin sin cos cos
2sin |
|
cos |
|
; |
|||
|
2 |
|
2 |
||||
|
|
|
|
|
|
||
2cos |
|
cos |
|
; |
|||
2 |
|
2 |
|||||
|
|
|
|
|
|
||
sin sin
cos cos
2sin |
|
cos |
|
; |
|
2 |
2 |
||||
|
|
|
2sin sin ; 2 2
83

tg tg
sin cos cos
;
tg tg
sin cos cos
.
Формулы преобразования произведения тригонометрических функций в сумму:
sin cos sin
sin cos cos
1 |
cos |
||
2 |
|||
|
|
||
1 |
|
cos |
|
2 |
|
||
|
|
||
1 |
sin |
||
2 |
|||
|
|||
cos ; cos ; sin .
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Функция
y arcsin x
На интервале |
|
|
|
|
|||
|
|
||
|
|
|
Арксинус числа
2 a
; |
|
функция |
y sin |
||
2 |
|
||||
|
|
|
|||
|
|
|
|
||
– это такое число |
|
x |
возрастает. |
из интервала
|
|
|
|
||
|
||
|
|
|
; |
|
2 |
||
|
|
, синус которого равен |
a . |
|
|
|||
|
|
||
2 |
|
|
|
|
|
|
|
|
|
; |
|
, |
|
arcsin a |
|
|
|
2 |
|
|||||
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
a 1. |
||
|
|
sin a, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
arcsin a arcsin a
 sin arcsin a a,
sin arcsin a a,  a
a 1
1
Функция
y arccos x
На интервале 0; функция y cos x
Арккосинус числа a – это такое число интервала 0; , косинус которого равен a .
убывает. из
|
|
0; , |
|
|
arccos a |
|
|
|
|
|
|
|
||
|
|
cos a, |
a |
1. |
|
|
|
|
|
arccos a arccos a |
|
|
||
 cos arccos a a,
cos arccos a a,  a
a 1
1
84

Функция y arctg x
На интервале ;
2
Арктангенс числа
|
функция |
y tg x |
|
|
|
2 |
|
|
a – это такое число |
||
возрастает.
из
|
|
|
; |
|
, тангенс которого равен |
интервала |
|
|
|||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
; |
|
, |
arc tg a |
|
|
2 |
|
||||
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
tg a. |
|
|
|
|||
arc tg a arc tg a |
|
|
|
|||||
tg arc tg a a |
|
|
|
|
|
|||
a
.
Функция
y arcctg x
На интервале 0; функция y ctg x |
убывает. |
|||
Арккотангенс числа a |
– это такое число |
из |
||
интервала 0; , котангенс которого равен a . |
|
|||
|
|
0; , |
|
|
arc ctg a |
|
|
|
|
|
|
|
||
|
|
ctg a. |
|
|
|
|
|
|
|
arcctg a arcctg a |
|
|
||
 ctg arc ctg a a
ctg arc ctg a a 
85

|
|
|
Приложение 4 |
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ |
|
||
1. ПРОИЗВОДНАЯ |
|
||
Число b называется пределом функции f x при x , стремящемся к |
a x a , если |
||
для любого 0 можно найти такое 0 , что при выполнении неравенства |
x a |
||
выполняется и неравенство f x b : |
lim f x b . Читают так: предел эф от икс при |
||
|
x a |
|
|
икс, стремящемся к a равен b . |
|
|
|
Производной функции y f x в точке x0 |
называется предел отношения |
||
приращения функции в точке x0 f x f x0 |
x f x0 к приращению аргумента |
||
x
, если приращение аргумента стремится к нулю |
x 0 : y |
|
|
f |
|
x lim |
f x |
|||||||||||||||
x |
||||||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
||
Для обозначения производной употребляют символы: |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
dy |
|
df |
|
x |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
, |
или |
f |
x , или dx |
, или |
dx . |
|
|
|
|
|
|
|
|
|||||||||
y |
|
|
|
|
|
|
|
|
|
|||||||||||||
Читают так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y |
|
- игрек штрих, |
|
|
|
|
|
|
|
f x |
- эф штрих от икс, |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
dy |
- дэ игрек по дэ икс, |
|
|
|
|
|
df x |
- дэ эф от икс по дэ икс. |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
dx |
|
|
|
|
|
dx |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Действие нахождения производной называется дифференцированием.
Производные некоторых элементарных функций:
 .
.
C 0 ,
C const
x 1
x |
n |
|
nx |
n 1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
, x 0 |
|||
|
|
x |
2 |
||
x |
|
|
|
|
|
|
|
|
1 |
, x 0 |
x |
|
|||
|
|
2 |
|
x |
Правило
U V U V
CU CU ,
C const |
|
|
|
|
|
UV |
U V UV |
|
2. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Как читать |
|
|
|
|
|
|
|
|
|
|
|
Пример |
|
|
|
|
|
|
|||||
Производная суммы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||
|
x |
|
|
x |
|
|
|
|
|
x |
1 |
|
|
|
|
||||||||
(разности) функций равна |
|
|
x |
|
2 |
|
x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
сумме (разности) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
производных функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Постоянный множитель |
|
5 |
|
|
|
|
|
|
5 |
|
|
|
|
5 1 |
|
|
|
4 |
|||||
можно выносить за знак |
4x |
|
4 x |
|
|
4 5x |
20x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
производной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная произведения |
x 2 x |
|
|
x 2 x |
|
x |
|
|
x 2 |
||||||||||||||
|
2 |
|
|
2 |
2 |
|
|
||||||||||||||||
равна сумме произведений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
производной первой функции |
|
|
|
|
|
|
|
2 |
2x x 2 |
|
|
|
|
||||||||||
на вторую и производной |
x |
|
2 x |
|
|
|
|
|
|||||||||||||||
1 |
0 x2 2x x 2 3x2 |
4x |
|||||||||||||||||||||
второй функции на первую |
|||||||||||||||||||||||
86

|
|
|
|
|
|
U |
|
U V V U |
|||
|
|
|
V |
2 |
|
|
|
||||
V |
|
|
|
||
Производная отношения двух функций равна дроби, в числителе которой разность произведений производной числителя на знаменатель и производной знаменателя на числитель, а в знаменателе – квадрат знаменателя функции
1x
|
1 |
||
x |
2 |
||
|
|||
|
|
||
|
1 x x 1 |
|
0 x 1 1 |
|
|||
x2 |
|
x2 |
|
||||
|
|
|
|||||
1
x2
3. ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1
2
3
4
5
6
7
8
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sin x |
|
cos x |
|
|
|
e |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arcsin x |
|
|
|
|
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
sin x |
|
a |
|
a |
|
ln a , a 0 |
|
|
|
|
|
|
|
|
arccos x |
|
|
|
1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
, x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||
tgx |
|
2 |
|
|
|
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
arc tgx |
|
|
|
|
2 |
|
|
|||||||||||||||||
|
|
|
cos |
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ctgx |
|
|
1 |
|
|
loga x |
|
|
1 |
|
, |
|
|
|
|
|
|
|
|
|
|
arc ctgx |
|
|
1 |
|
|
||||||||||||||||||
|
|
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
x ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
x 0, a 0, a 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
4. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
Таблица производных функций ( U функция от x ): |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная функции |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
y C const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y C 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y U n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
U |
n |
|
nU |
n 1 |
U |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
1 |
|
|
|
1 |
U , |
U 0 |
|
|
|
|
|
|||||||||||||
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y |
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
U |
|
|
|
1 |
|
U , U |
|
0 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
U |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y aU |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
U |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y a |
|
|
a ln a U , a |
|
|
|
|
|
|
|||||||||||||||
y eU |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
U |
U |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y e |
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y loga U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y loga U |
|
|
|
|
U , |
|
U 0, a 0, a 1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U ln a |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
87

9
10
11
12
13
14
15
16
17
y lnU
y sinU
y cosU
y tgU
y ctgU
y arcsinU
y arccosU
y arctgU
y ar c ctgU
|
|
1 |
U |
, U 0 |
|
||||||||||
y lnU |
|
|
|||||||||||||
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
cosU |
U |
|
|
|
|
|||||||||
y sinU |
|
|
|
|
|||||||||||
|
sinU U |
|
|
||||||||||||
y cosU |
|
|
|||||||||||||
|
|
|
1 |
|
|
|
|
U |
|
|
|
|
|||
y tgU |
|
2 |
U |
|
|
|
|
|
|||||||
|
cos |
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
U |
|
|||||||||
y ctgU |
2 |
U |
|
||||||||||||
|
|
|
sin |
|
|
|
|
|
|
||||||
y arcsinU |
|
|
|
|
1 |
|
|
|
U |
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
1 U 2 |
|||||||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
U |
|||||
y arccosU |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 U |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
U |
|
|
|||||||
y arctgU |
|
|
|
|
2 |
|
|||||||||
|
|
|
1 U |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
U |
||||||
y arc ctgU |
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
1 U |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
5. МЕХАНИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Механический смысл производной: скорость движения |
|
является производной |
|||||||||
от пути S по времени t : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dS |
S |
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
или от координаты x по времени t |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
x |
|
. |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
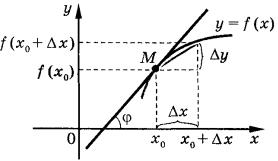
Геометрический смысл производной: значение производной |
в |
точке x0 равно |
|||||||||
тангенсу угла наклона касательной к графику функции в точке |
x0 |
, |
т.е. |
равно угловому |
|||||||
коэффициенту k касательной: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||
|
|
k tg f x0 |
|
|
|
|
|||||
Уравнение касательной к графику функции y f x в точке с абсциссой x0 :
 y f x0 f x0 x x0
y f x0 f x0 x x0  .
.
88
89
|
СОДЕРЖАНИЕ |
|
Введение |
|
3 |
|
Механика |
|
Глава 1 |
Кинематика |
4 |
|
|
|
1.1 |
Физические тела и механическое движение |
4 |
1.2 |
Материальная точка. Траектория |
5 |
|
Упражнение 1 |
6 |
1.3 |
Скорость. Равномерное прямолинейное движение |
6 |
1.4 |
Измерение физических величин. СИ |
8 |
1.5 |
Алгоритм решения задач |
10 |
|
Упражнение 2 |
11 |
1.6 |
Скалярные и векторные физические величины |
12 |
|
Упражнение 3 |
16 |
1.7 |
Ускорение. Равнопеременное прямолинейное движение |
17 |
1.8 |
Графики скорости для прямолинейного движения |
20 |
|
Упражнение 4 |
21 |
1.9 |
Свободное падение |
22 |
1.10 |
Движение тела, которое брошено горизонтально на высоте |
23 |
|
h |
|
1.11 |
Движение тела, которое брошенного под углом к горизонту |
24 |
|
Упражнение 5 |
24 |
1.12 |
Равномерное движение тела по окружности |
25 |
|
Упражнение 6 |
27 |
Глава 2 |
Динамика |
28 |
2.1 |
Законы Ньютона |
28 |
2.2 |
Силы в механике |
29 |
2.3 |
Примеры решения задач на законы Ньютона |
31 |
|
Упражнение 7 |
36 |
Глава 3 |
Элементы статики |
37 |
3.1 |
Равновесие твѐрдых тел, которые не имеют оси вращения |
37 |
3.2 |
Равновесие твѐрдого тела, которое имеет закреплѐнную ось |
|
|
вращения |
37 |
|
Упражнение 8 |
38 |
3.3 |
Гидроаэростатика |
39 |
|
Упражнение 9 |
42 |
90
Глава 4 |
Законы сохранения |
44 |
4.1 |
Закон сохранения импульса |
44 |
|
Упражнение 10 |
45 |
4.2 |
Работа. Мощность. КПД |
46 |
4.3 |
Энергия. Закон сохранения энергии |
47 |
|
Упражнение 11 |
49 |
Глава 5 |
Механические колебания и волны |
52 |
5.1 |
Свободные колебания. Характеристики |
механических 52 |
|
колебаний |
|
5.2 |
Гармонические колебания |
57 |
5.3 |
Энергия колебательного движения |
61 |
|
Упражнение 12 |
62 |
5.4 |
Механические волны |
64 |
5.5 |
Звук |
65 |
|
Упражнение 13 |
66 |
Приложения |
|
|
1 |
Элементы векторной алгебры в физике |
68 |
2 |
Движение жидкостей. Уравнение Бернулли |
76 |
3 |
Тригонометрические функции |
79 |
4 |
Дифференциальное исчисление |
86 |
91
