Adaptatsionny_Kurs_Kulik

Глава 5. Механические колебания и волны

Колебательное движение (или колебания) широко распространено в природе и технике, биологии и медицине. Например: мы наблюдаем колебания воды в море, маятника в часах, струны в музыкальном инструменте, биения сердца, вибрации голосовых связок и т.д. В зависимости от физической природы различают механические и электромагнитные колебания, которые происходят по одинаковым законам и описываются аналогичными математическими уравнениями.

5.1. Свободные колебания. Характеристики механических колебаний

Движение, которое точно повторяется через равные промежутки времени (период) называется периодическим. Например, периодическим движением является равномерное движение тела по окружности (см. § 1.12). Но это движение происходит в одном направлении. Колебательное движение – это движение, которое тело совершает поочерëдно в двух противоположных направлениях.

Механические колебания или колебательные движения – это поочерëдные периодические движения тела в двух противоположных направлениях.

Характерным примером колебательного движения является движение маятника. Маятник – это твѐрдое тело, которое под действием приложенных сил совершает колебания около неподвижной точки или оси.

Самый простой маятник можно сделать из небольшого груза и длинной нити (рис. 36, а). Если отклонить груз на малый угол и отпустить, то он начнëт совершать колебания около положения равновесия (среднее положение груза на рисунке 36, а).

Рис. 36

На рисунке (36, б) показан другой вид маятника – пружинный. В начальном положении тело, которое подвешено на пружине, находится в равновесии. Выведем тело из равновесия (растянем пружину) и отпустим – тело на пружине начнëт совершать колебания вверх–вниз относительно положения равновесия.

52

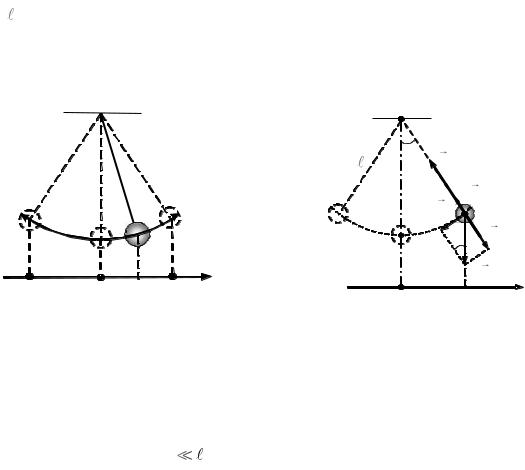
Колебательное движение тела происходит в колебательной системе «тело– Земля–нить (или пружина) – штатив (опора)», в которой действуют внутренние силы – сила тяжести и сила натяжения нити (или сила упругости для пружинного маятника). Такое движение – пример свободных механических колебаний.

Свободными колебаниями называются колебания в системе, которую вывели из положения равновесия и предоставили действию внутренних сил.

Если на систему действует внешняя периодическая сила, то такие колебания называются вынужденными колебаниями.

В рассмотренных примерах система совершала колебания около положения устойчивого равновесия. Равновесие называется устойчивым, если при выведении системы из этого положения, равнодействующая всех сил, которые приложены к телу, стремится вернуть систему в это же положение. В данном случае равнодействующую силу называют возвращающей силой. Любая система, которая может совершать свободные колебания, имеет положение устойчивого равновесия.

Свободные колебания будут существовать долго, если силы сопротивления в системе малы. В зависимости от значения этих сил, свободные колебания делят на незатухающие (силы сопротивления близки к нулю и энергия системы практически не изменяется) и затухающие (энергия системы расходуется на совершение работы против сил сопротивления). Свободные незатухающие колебания называются

собственными колебаниями.

Изучим характеристики колебательного движения на примере математического маятника. Математический маятник – это идеализированная колебательная система:

положения равновесия) – это амплитуда колебаний. Будем рассматривать колебания с малой амплитудой, так что x и угол отклонения маятника от вертикали –

53

F2 x k x .

Преобразуем уравнение движения

где – циклическая частота (или круговая частота).

Окончательно уравнение движения математического маятника принимает

вид:

ax 2 x .

54

Математический маятник совершает свободные колебания, ускорение которых пропорционально смещению.

Коэффициент k характеризует свойства данной колебательной системы, и для математического маятника этот коэффициент зависит от массы маятника и длины

подвешено на абсолютно упругой пружине (силы сопротивления не учитываем, массой пружины можно пренебречь по сравнению с массой тела m ). Тело совершает колебания под действием силы упругости пружины, поэтому такие колебания называются упругими колебаниями.

Начало оси координат (точка O ) совпадает с положением равновесия тела на пружине (точкой A ). Если сместить тело в точку B , а затем отпустить его, то оно будет совершать колебательные движения около положения равновесия под действием силы упругости, которая стремится вернуть тело в положение равновесия (возвращающей силы). Достигнув положения равновесия, тело не останавливается, а по инерции проходит его за счѐт кинетической энергии, которой обладает движущееся тело. При дальнейшем движении тело начинает сжимать пружину, и в ней снова возникает сила упругости, которая направлена против сжатия пружины. В

колебательные движения.

Рис. 38

где 0 – удлинение пружины, которое соответствует положению равновесия тела; k – коэффициент упругости пружины. Если сместить тело в положение, которое

55

характеризуется координатой x , то удлинение пружины станет равным ( 0 + x ).

где ω – циклическая частота (или круговая частота).

Получим уравнение движения пружинного маятника в виде:

ax 2 x .

Ускорение, с которым колеблется тело на пружине, пропорционально его смещению из положения равновесия.

Для сравнения различных колебательных движений вводят основные характеристики колебаний, т.е. физические величины, которые относятся к колебанию в целом и не изменяются на протяжении всего колебания. При колебаниях математического маятника материальная точка движется по части окружности. А мы знаем, что равномерное движение точки по окружности можно рассматривать как точное повторение одного и того же цикла движений – полного оборота. Для собственных колебаний маятника такой цикл движений называется полным колебанием. Продолжительность (время) одного цикла называется периодом.

Период колебаний – это время, за которое совершается одно полное колебание. Символ периода колебаний – T , единица – секунда (с).

Если за время t совершается N полных колебаний, то период колебаний

равен:

T Nt .

Соответственно, частотой колебаний называется величина

56

равная числу полных колебаний, которые совершаются за единицу времени.

Если система совершает колебания с частотой 1 Гц, это значит, что она совершает одно колебание в секунду.

Циклической или круговой частотой колебаний называется величина, равная

период собственных колебаний пружинного маятника

определѐнным законом. Колебания системы, которые происходят по закону синуса

на рис. (39, б). Пусть в момент времени t = 0 (начало колебательного движения) точка B находилась в точке O , что соответствует, например, положению равновесия рассмотренного в § 5.1 математического маятника. При этом положение точки A совпадало с положением точки D , угол = 0 (рис. 39, а).

57

гармонических колебаний и описывает колебательное движение точки, которая в момент начала отсчëта времени ( t = 0) находилась в положении равновесия (рис. 70, а) (или была максимально смещена из положения равновесия (рис. 40, б)).

смещена из положения равновесия (рис. 41), то в общем виде закон гармонических колебаний запишется так:

x xm sin t 0 или x xm cos t 0 ,

58

Рис. 41

за начало отсчѐта. Фаза колебаний определяет при заданной амплитуде состояние колебательной системы (смещение, скорость, ускорение) в любой момент времени.

в противофазе (рис. 72).

Собственные колебания являются гармоническими колебаниями. Чтобы убедиться в этом, вспомним (см. §1.2), что по определению

Рис. 42

59

т.е. ускорение гармонических колебаний пропорционально смещению.

Мы получили уравнение, которое имеет такой же вид, как и уравнения движения пружинного и математического маятников. Из него следует

дифференциальное уравнение гармонических колебаний

Собственные гармонические колебания совершаются под действием упругих (или квазиупругих) внутренних сил

или косинуса, т.е. являются периодическими функциями времени. Говорят: собственные колебания совершаются под действием периодической внутренней силы.

Если на систему действует внешняя периодическая сила (вынуждающая сила), которая изменяется по закону синуса или косинуса, то система совершает вынужденные гармонические колебания. Частота вынужденных колебаний всегда равна частоте изменения вынуждающей силы. Амплитуда вынужденных колебаний зависит от частоты изменения вынуждающей силы. Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты изменения внешней периодической силы к частоте собственных колебаний системы называется

резонансом.

Резонанс используют в устройстве многих приборов. Например: приборы для настройки музыкальных инструментов, генераторы для настройки маятников часов. Однако резонанс может быть опасен и его стараются устранить во многих технических конструкциях. Например: собственная частота моста должна значительно отличаться от частоты воздействий со стороны движущегося транспорта; собственная частота здания должна отличаться от частоты колебаний земной поверхности и частоты воздействий со стороны движущихся людей в здании.

60

5.3. Энергия колебательного движения

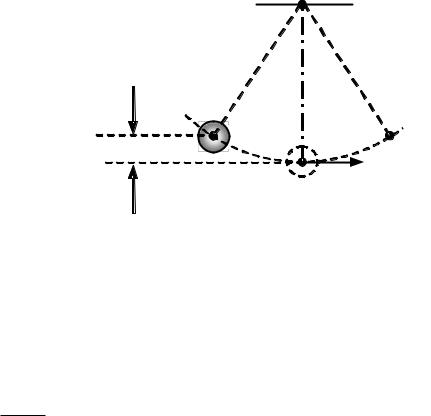
Рассмотрим преобразования энергии механических колебаний на примере математического маятника. Для возникновения колебаний маятника его надо вывести из положения равновесия на некоторую высоту hmax . При этом совершается работа по

перемещению маятника, и он приобретает потенциальную энергию. В течение одного периода колебаний скорость маятника равна нулю в двух положениях наибольшего отклонения от равновесия (точки A и B на рис. 43), которые находятся на высоте hmax от уровня положения равновесия.

Рис. 43

На этом уровне потенциальную энергию примем равной нулю. Этим

механической энергии в другой вид: из потенциальной энергии в кинетическую энергию и обратно. В крайних точках отклонения (точки A и B ) маятник имеет максимальную величину потенциальной энергии, а при движении через положение равновесия (точка O ) маятник обладает максимальным значением кинетической энергии. В остальных положениях движения маятник имеет энергию двух видов – потенциальную и кинетическую.

Закон сохранения полной механической энергии колебательного движения:

сумма кинетической Ек и потенциальной Еп энергий остаѐтся постоянной в любой момент времени колебательного движения

E Eк Еп Еп max Ек max .

61