
Лекции Соболева часть 3
.pdf
38 Лекция 5 - 9
|
|
|
∂u =( u l ) = |
|
u |
|
|
|
l |
|
cosϕ = |
|
grad u |
|
cosϕ, |
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
∂ |
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где ϕ - угол между единичным вектором l0 данного направления l |
и векто- |
||||||||||||||||||||||
ром градиента grad u . |
∂u = 0 . |
Если grad u ≠ 0 , то ∂u < |
|
|
|
|
|
||||||||||||||||
Если grad u = 0 , то |
|
grad u |
|
|
для всех |
||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
∂l |
|
|
|
|
|
|
|
|
|
|
∂l |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
векторов l , за исключением вектора l , направленного в сторону grad u . |
|||||||||||||||||||||||
Вывод: ∂u |
= |
|
grad u |
|
cosϕ . Производная по направлению вектора l в |
||||||||||||||||||
|
|
||||||||||||||||||||||
∂l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точке P(x, y, z) |
равна проекции градиента на данное направление. |
|
|||||||||||||||||||||
5.4.3. Свойства градиента
Пусть задан градиент поля и производная по направлению:
∂u ∂u ∂u |
|
|
|
∂u 2 |
|
∂u 2 |
∂u 2 |
|||||||
|
|
|
||||||||||||
u = |
|
, |
|
, |
|
, |
u |
= |
|
|
|
|
+ |
. |
|
|
+ |
|
|||||||||||
|
∂x |
|
∂y |
|
∂z |
|
|
|
|
∂x |
|
∂y |
|
∂z |
|
|
|
|
|
||||||||||
1.Максимальное значение производной по направлению равно модулю
градиента: ∂∂ul = gradu cosϕ ; ϕ → 0;cosϕ →1 max ∂∂ul = grad u .
2.Вектор u направлен в сторону возрастания поля.
3.Вектор u всегда нормален к поверхности (линии) уровня поля (эквипотенциальной поверхности).
Доказательство:
Пусть u = u(x, y, z) скалярное поле и u(x, y, z) = c - уравнение поверхности уровня. Выберем P {u(x, y, z) = c}, которую обозначим P(x, y, z) , и проведём касательную плоскость к поверхности, описываемой уравнением
F (x, y, z) = u(x, y, z) −c = 0 ;
∂∂Fx (x − x) + ∂∂Fy ( y − y) + ∂∂Fz (z − z) = 0 - уравнение касательной плоскости;
∂∂ux (x − x) + ∂∂uy ( y − y) + ∂∂uz (z − z) = 0 .
Тогда вектор нормали касательной плоскости имеет вид:
|
∂u |
, |
∂u |
, |
∂u |
|
, |
n = |
∂u i + |
∂u |
j + |
∂u k = u . |
n = |
|
|||||||||||
|
∂x |
|
∂y |
|
∂z |
|
|
|
∂x |
∂y |
|
∂z |
Теория поля |
39 |
!Свойства 1-3 дают инвариантное (не зависящее от системы координат) определение градиента, т.е. утверждают, что независимо от системы ко-
ординат u указывает величину и направление наибольшего возраста-
ния скалярного поля в точке: grad u = mах ∂u .
∂l
Дифференциальные свойства градиента:
•Если скалярное поле есть сумма двух полей:
f(x, y, z) = u(x, y, z) + v(x, y, z) , то f = (u + v) =u +v .
•(u v) = ( u)v +u( v) .
•c u = c u .
•f (u) = fu′ u - градиент сложной функции.
•f (u,v) = fu′ u + fv′ v .
Пример:
Найти |
наибольшую крутизну подъёма поверхности u = x y в точке |
||||||||
Р (2,2,4). |
∂u |
||||||||
Решение: |
|
grad u |
|
|
|||||
|
|
||||||||
|
|
= mах |
. |
||||||
|
|
|
|
|
|
|
|
|
∂l |
u = u′x i + u′y j + u′z k = yx y −1 i + x y ln x j + 0k . |
|||||||||
|
u |
|
= |
( yxy−1 )2 + (xy ln x)2 |
= (2 2)2 + (4ln 2)2 = 4 1+ ln2 2 . |
||||
|
|
||||||||
Пример:
Найти нормаль к поверхности u = x2 + y 2 + z 2 в точке Р (1,1,1). Решение:
По свойству |
3: |
n u , grad u = 2xi + 2 y j + 2zk , u = 2xi +2 y j + 2zk = |
|||||||
|
|
={2, 2, 2} n0 ={ |
1 |
, |
1 |
, |
1 |
}. |
|
= 2i + 2 j + 2k |
P(1,1,1) |
||||||||
3 |
3 |
3 |
|||||||
|
|||||||||
Пример:
Найти градиент функции r = 
 (x − x0 )2 + ( y − y0 )2 + (z − z0 )2 (модуль радиус-вектора).
(x − x0 )2 + ( y − y0 )2 + (z − z0 )2 (модуль радиус-вектора).
Решение:
P0 -фиксированная точка, P(x,y,z) – изучаемая точка поверхности.
grad r = ∂r i + ∂r |
j + ∂r k = |
{x − x0 ; y − y0 ; z − z0} |
= r |
|
|||
∂x ∂y |
∂z |
(x − x0 )2 +( y − y0 )2 + (z − z0 )2 |
0 |
|
- единичный вектор вектора P0 P .
40 |
|
|
|
|
|
|
|
|
Лекция 5 - 9 |
||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
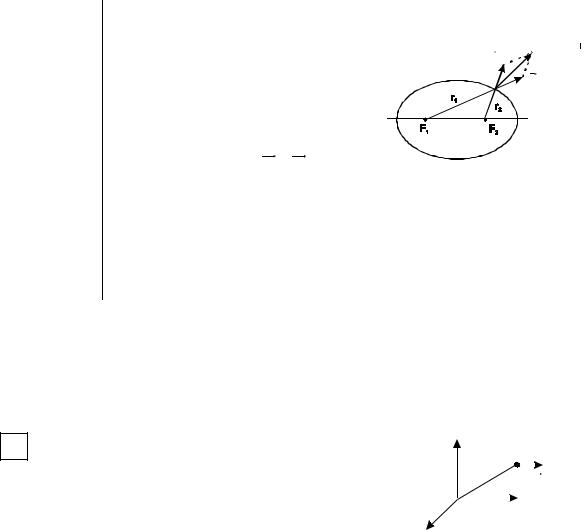
Найти градиент скалярной функции |
|
|
|
|
|
|
||||
|
u (P) = r1 + r2 , |
где |
r1 , |
r2 - |
рас- |
|
|
|
|
grad (r1 r2 ) |
|
|
0 |
|
|||||||||
|
|
|
|
||||||||
|
стояния от точки Р до фиксирован- |
r2 |
|||||||||
|
|
|
|
0 |
|
|
|||||
|
ных точек F1 , |
F2 . Линии уровня |
|
|
r1 |
||||||
|
|
|
|
|
|
|
|||||
|
этой функции – эллипсы. |
|
|
|
|
|
|
|
|||
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
Имеем: grad (r + r ) = r 0 |
+ r 0 , |
т.е. |
|
|
|
|
|
|
||
1 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
градиент равен диагонали ромба, построенного на ортах радиус- |
||||||||||
|
векторов, проведенных к точке Р из фокусов F1 |
и F2 . Нормаль к эллип- |
|||||||||
су в какой-либо точке делит пополам угол между радиус-векторами, проведёнными в эту точку.
Физическая интерпретация: луч света, вышедший из одного фокуса, попадает в другой фокус.
5.5. Векторное поле
ОЕсли с каждой точкой P(x; y; z) простран-
ственной области G связана векторная функция её радиус-вектора a = a (P ) , то го-
ворят, что в области G задано векторное поле.
Векторное поле определяется тремя скалярными характеристиками – координатами вектора
Z |
P(x,y,z) |
||
|
|
|
|
|
|
a(P) |
|
|
|
Y |
|
X |
|
|
|
a , |
a ={ax , ay , az } или |
||
a = ax i + ay j + az k , где ax = ax (x, y, z) , ay = ay (x, y, z) , az = az (x, y, z) - проек-
ции векторного поля на оси координат или компоненты вектор-функции. Будем считать, что они непрерывны и дифференцируемы по всем переменным.
Теория поля |
41 |
5.5.1. Векторные линии
Векторное поле можно изобразить графиче-
ски, указав положение вектора a в некоторых точках.
ОВекторной линией поля a = a (P) в области
G называется кривая, в каждой точке которой
вектор a направлен по касательной к этой кривой.
Найдём уравнения векторных линий. Предположим, что векторные линии есть прямые,
тогда их уравнения: |
x − |
x |
= |
y − |
y |
|
= |
z − |
z |
|
, |
||
|
|
|
|
|
|
|
|
||||||
|
|
|
ax |
ay |
az |
||||||||
∆x = |
∆y = |
∆z . Так как любую кривую можно на |
|||||||||||
ax |
ay |
az |
|
|
|
|
|
|
|
|
|
|
|
бесконечно малом участке величины
dr = (dx;dy;dz) заменить отрезком касательной, а направление касательной совпадает с направле-
нием a , то уравнения векторной линии имеют вид:
dx = dy = dz . ax ay az
На самом деле речь идет о системе дифференциальных уравнений первого порядка.
dy |
= |
ay |
; |
dz |
= |
a |
z |
; |
dz |
= |
a |
z |
. |
|
dx |
ax |
dx |
ax |
dy |
|
|
|
|||||||
|
|
|
|
|
ay |
|
||||||||
Общее решение этой системы: |
ϕ (x, y, z) = C ; |
|||||||||||||
|
1 |
|
1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
ϕ2 (x, y, z) = C2 , |
||||
определяет двухпараметрическое семейство линий и дает совокупность всех векторных линий поля.
Z |
a(P) |
|
a(P) |
||
|
P(x, y, z) P(x, y,z)
Y
X
a ( P ) Z  P(x, y, z)
P(x, y, z) 
P(x, y, z)
Y
X
 Г
Г
ОВекторной трубкой называется совокупность всех векторных линий, пересекающих часть некоторой лежащей в векторном поле поверхности Σ, ограниченной замкнутым контуром Г.
42 |
|
|
|
|
Лекция 5 - 9 |
|
|
5.5.2. Плоское векторное поле |
|
|
|
|
|
|
|
Векторное поле называется плоским, если все век- |
|
|
||
|
О |
Z |
|
|||
|
|
торы лежат в параллельных плоскостях. |
a(P) |
|||
|
|
|||||
|
|
dx |
dy |
dz |
|
|
|
|
Уравнение векторных линий ax |
= ay = |
0 . |
|
a(P) |
|
|
В плоском поле векторные линии есть плоские |
|
Y |
||
|
! |
X |
||||
|
|
|||||
|
|
кривые y =ϕ(x). |
|
|
|
|
|
|
|
|
|
||
Пример:
Найти векторные линии поля, если поле задано вектором: a = −yi + xj + bk в точке Р (1,0,0)
Решение:
−dxy = dyx = dzb .
1). |
|
dx |
|
= |
dy |
, |
xdx = −ydy , |
xdx + ydy = 0 ; |
|
|||||||||||
|
− y |
|
x |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x2 |
+ |
y2 |
|
|
= c 2 |
; c = |
2c ; |
x2 + y2 = (c |
|
)2 |
- уравнение окружности. |
||||||||
|
|
|
|
|
|
2 |
||||||||||||||
2 |
2 |
|
|
1 |
|
2 |
|
1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x = c2 cos t; |
|
|
|
||||||||
2). |
|
dy |
= |
|
dz |
, |
bdy = xdz |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x |
|
|
b |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y = c2 sin t; |
|
|
|
||||||
bc2 costdt = c2 cos tdz , dz = bdt , |
|
|
||||||||||||||||||
|
z = bt + c1; |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = c2 cos t |
|
|
|
|
|
|
|
|
|||||||||||
|
y = c |
|
|
sin t; |
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В точке P (1,0,0): |
|
|
|
|
|
|
||||||||||||||
|
1 |
= c2 |
|
|
|
|
|
|
|
|
c1 = 0 |
|
x = cos t |
|
|
|
||||
|
|
= 0 |
|
|
|
|
|
|
|
|
|
|
- |
|
|
|||||
|
0 |
|
|
|
|
|
|
|
|
c |
=1 |
|
y = sin t |
|
|
|||||
|
|
= 0 + c1 |
|
|
|
|
|
|
||||||||||||
|
0 |
|
2 |
|
|
z = bt |
|
|
|
|||||||||||
уравнение винтовой линии.
6. Поверхностные интегралы
6.1. Односторонние и двусторонние поверхности
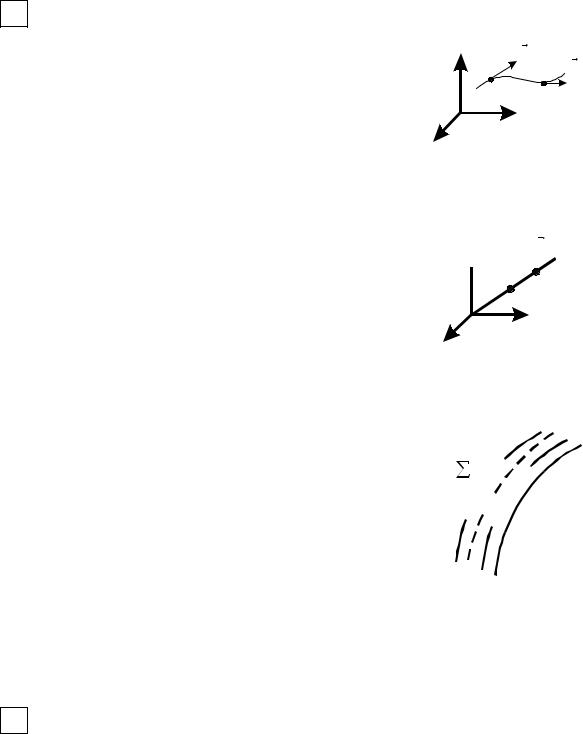
Рассмотрим гладкую и незамкнутую поверхность ∑, ограниченную ку- сочно-гладким контуром γ . Это означает, что для уравнения поверхности существуют частные производные по всем переменным. В точке Р проведём

Теория поля |
43 |
нормаль n к поверхности. Через точку P проведем замкнутый контур Г, не имеющий общих точек с границей γ .
При обходе контура возможны две ситуации: |
|
n |
а) нормаль к поверхности n при возвращении в |
Z |
Г |
точку P сохранит свое направление; |
|
|
|
|
|
б) при непрерывном движении вдоль замкнутого |
|
|
контура Г, непрерывно меняясь по направлению, нор- |
|
Y |
маль изменит направление на противоположное при |
|
|
X |
|
|
возвращении в исходную точку. |
|
|
|
|
|
В случае «а» поверхность называется двусто- |
|
|
ронней, в случае «б» – односторонней. Совокупность точек поверхности с определенным направлением нормали n называется стороной поверхности.
!Классическим примером односторонней поверхности является лист Мебиуса.
6.2. Площадь поверхности
Пусть ∑ - незамкнутая гладкая поверхность. Разобьем ее на участки ∆∑i , (i =1,..., n ), с помощью сети кривых. Выберем в каждом участке ∆∑i точку Pi . Проведем в точке Pi касательную плоскость к поверхности ∑ и спроектируем ∆∑i на касательную плоскость. На проекции получим плоскую фигуру с площадью ∆Si′.
|
Площадью |
поверхности |
S называется предел суммы площадей |
∆Si′ |
|
О |
|||||
(i =1,..., n ), |
при условии, |
что диаметры всех частей разбиения |
∆∑i |
||
|
n
стремятся к нулю: S = lim ∑∆Si′.
∆∑i →0 i=1
! Поверхность, имеющая площадь, называется квадрируемой.
Пусть поверхность задается явным уравнением z = z (x, y), где z (x, y) -
непрерывно дифференцируемая функция, и однозначно проектируется в плоскую область Dxy на координатной плоскости Oxy . Нормаль n к
поверхности ∑, как вектор, ортогональный к касательной плоскости, имеет компоненты: n = ∂∂xz , ∂∂yz , −1 , и направляющие косинусы нормали n равны:
cos(n,i )= cosα = ± |
|
|
∂z |
|
|
|
|
|
|
∂x |
|
|
|
, |
|
|
|
∂z 2 |
|
∂z |
2 |
||
1 |
|
|
|||||
+ |
|
+ |
|
|
|
||
|
|
|
∂x |
|
∂y |
|
|
44 |
|
|
|
|
|
|
|
|
|
Лекция 5 - 9 |
cos(n, j )= cos β = ± |
|
|
∂z |
|
|
|
|
|
||
|
|
∂y |
|
|
|
|
, |
|||
|
|
∂z 2 |
|
∂z |
2 |
|
||||
1 |
|
|
|
|||||||
+ |
|
+ |
|
|
|
|
||||
|
|
|
|
∂x |
|
∂y |
|
|
|
|
cos(n, k )= cosγ = ± |
|
|
|
1 |
|
|
|
. |
||
|
|
∂z |
2 |
|
∂z |
2 |
||||
1 |
|
|
|
|
||||||
+ |
|
|
+ |
|
|
|
|
|||
|
|
|
|
∂x |
|
|
∂y |
|
|
|
Выбор знака перед радикалом соответствует острому или тупому углу нормали n с соответствующей осью координат и определяет сторону поверхности ∑.
Спроектируем элементы ∆Si′ на касательной плоскости на
координатную плоскость Oxy , площадь проекции |
|
|
|
|||||||||||||||||
∆Si = ∆Si′ |
|
cosγ |
|
= |
|
|
|
|
∆Si′ |
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
∂z 2 |
|
∂z 2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
∂y |
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆Si′ = |
|
|
∆S |
i |
|
|
= ∆Si |
|
|
|
|
∂z 2 |
|
∂z 2 |
||||||
|
|
|
|
|
|
1 |
+ |
+ |
|
|
, |
|||||||||
|
|
cosγ |
|
|
|
|||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
∂y |
|
|||||
и предел, фигурирующий в определении площади поверхности S , представляет собой двойной интеграл по области Dxy
S = ∫∫ |
|
|
dx dy |
|
|
|
= ∫∫ |
∂z 2 |
∂z 2 |
|
||||||
|
|
|
|
|
|
|
|
|
1+ |
+ dx dy . |
||||||
|
|
|
cosγ |
|
||||||||||||
|
|
|||||||||||||||
|
Dxy |
|
|
|
|
|
|
Dxy |
∂x |
∂y |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Если уравнение поверхности Σ дано в виде x = x(y, z) или y = y (x, z), |
||||||||||||||||
то площадь может быть представлена как |
|
|
||||||||||||||
S = ∫∫ |
|
|
dy dz |
|
|
|
= ∫∫ |
∂x 2 |
∂x 2 |
|
||||||
|
|
|
|
|
|
|
1+ |
+ dy dz |
|
|||||||
|
|
cosα |
|
|
|
|
||||||||||
|
|
|
|
|||||||||||||
|
Dyz |
|
|
|
|
|
|
Dyz |
∂y |
∂z |
|
|||||
или |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ |
|
|
|
|
dx dz |
|
|
|
|
∫∫ |
∂y 2 |
∂y 2 |
|
||
|
|
|
cos β |
|
|
|
|
∂x |
∂z |
|
||||||
S = |
Dxz |
|
|
|
|
|
= |
Dxz |
1+ |
+ dx dz |
, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где Dyz и Dxz - проекции поверхности Σ на плоскости Oyz и Oxz .
Теория поля |
45 |
6.3. Система координат и ориентация поверхности
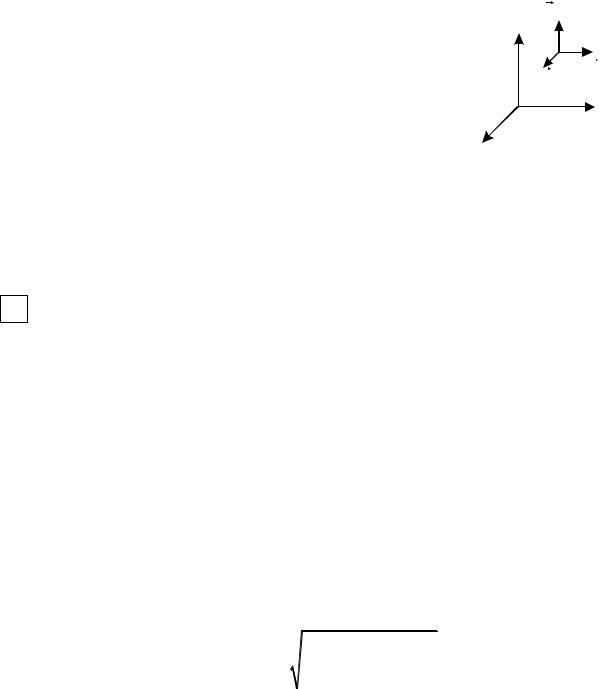
Введем систему координат в пространственной области G. Система векторов a,b, c образует правую тройку, если поворот от a к b , если наблюдать его из конца вектора c , происходит против часовой стрелки, в противном случае тройка называется левой. В дальнейшем будем работать с правой системой координат. В случае незамкнутой поверхности сторону можно определить, определив направление обхода контура.
Выберем определенную сторону незамкнутой |
c |
|
двусторонней поверхности, а в ней замкнутый контур |
|
|
Z |
|
|
Г. Он ориентирован положительно, если обход со- |
|
|
вершается против часовой стрелки (+), и ориентиро- |
a |
b |
ван отрицательно, если обходится по часовой стрел- |
|
|
|
|
|
ке. |
|
Y |
Построим в точке поверхности, лежащей внутри |
X |
|
контура, нормаль к поверхности и воспользуемся: |
|
«правилом буравчика».
Поверхность является положительно ориентированной, если при обходе контура Г в положительном направлении движение винта совпадает с направлением нормали. Если движение винта противоположно направлению нормали, то поверхность отрицательно ориентирована.
!Для замкнутой поверхности считается, что внешняя поверхность ориентирована положительно, а внутренняя - отрицательно.
6.4. Поверхностный интеграл 1-го рода
(Рассматривался в курсе «Интегралы по фигуре». Краткие сведения).
Рассмотрим поверхность ∑, в каждой точке которой задана функция: f (P) = f (x, y, z) . Если поверхность однозначно проектируется на плоскость
Oxy в область Dxy и задана уравнением z = f (x, y) , то
∫∫ f |
(x, y, z)dσ =∫∫ f (x, y, z(x, y)) |
|
dxdy |
= |
|||||
|
cos(γ ) |
|
|||||||
|
|
||||||||
Σ |
|
Dxy |
|
|
|
|
|
|
|
|
∂z 2 |
|
∂z 2 |
|
|||||
= ∫∫ |
|
|
|||||||
f (x, y, z(x, y)) 1 + |
|
+ |
|
|
dxdy . |
||||
D |
xy |
|
∂x |
|
∂y |
|
|||
|
|
|
|
|
|
|
|
|
|

46 |
Лекция 5 - 9 |
6.5. Поверхностный интеграл 2-го рода
Рассмотрим ориентированную поверхность ∑. Спроектируем элемент поверхности ∆Σi на координатную плоскость Oxy , обозначив площадь про-
екции ∆Si . На каждом элементе поверхности ∆Σi выберем произвольную точку Pi ∆Σi , вычислим в ней значение функции и умножим его на площадь проекции. Сложив эти произведения, получим интегральную сумму:
n |
n |
∑ f (Pi ) ∆Si =∑ f (xi , yi , zi ) ∆Si . |
|
i=1 |
i=1 |
Конечный предел этой интегральной суммы при стремлении диаметра разбиения к нулю называется поверхностным интегралом 2-го рода от функции f (x , y , z) по определенной стороне поверхности и обозначается:
Ixy = ±∫∫ f (P)dxdy =± ∫∫ f (x, y, z)dxdy .
ΣΣ
Знак (+) соответствует положительной (внешней), а (–) отрицательной (внутренней) сторонам поверхности.
Если на данной поверхности заданы другие функции f1 (x, y, z) , f2 (x, y, z) , то проектирование на другие координатные плоскости дает интегралы:
I yz = ±∫∫ f1 (x, y, z)dydz; |
Ixz =± ∫∫ f2 (x, y, z)dxdz . |
Σ |
Σ |
Соединение этих интегралов дает общее выражение для поверхностного интеграла второго рода:
I = ±∫∫ f (x, y, z)dxdy + f1 (x, y, z)dydz + f2 (x, y, z)dxdz .
∑
Между поверхностными интегралами 1-го и 2-го рода существует сле- ! дующая связь:
∫∫ f (x, y, z) cosγdσ = ± ∫∫ f (x, y, z)dxdy ,
Σ |
Σ |
причем при интегрировании по положительной стороне поверхности: cosγ > 0; cosγdσ = +dxdy ,
а по отрицательной: cosγ < 0;cosγdσ = −dxdy .
!Поверхностные интегралы 2-го рода обладают всеми свойствами двойных интегралов.
Теория поля |
47 |
Поверхностный интеграл второго рода может быть записан в более ком- |
|
пактном виде. Пусть |
a ={ax , ay , az }, где ax = ax (x, y, z) , ay = ay (x, y, z) , |
az = az (x, y, z) - векторное поле. Для координат этого вектора можно составить поверхностный интеграл второго рода, проектируя каждую координату вектора на соответствующую координатную плоскость:
I = ∫∫ax (x, y, z)dydz + ay (x, y, z)dxdz + az (x, y, z)dxdy =
Σ
= ∫∫(ax (x, y, z)cosα + ay (x, y, z)cos β + az (x, y, z)cosγ )dσ .
Σ
Так как n0 - единичный вектор нормали к выбранной стороне поверхности
Σ, n0 ={cosα,cos β,cosγ}, то I = ∫∫(a(x, y, z) n0 )dσ .
|
Σ |
Вводя dσ = n0 dσ |
- векторный элемент площади поверхности, направлен- |
ный по нормали n0 |
и имеющий длину dσ , получаем I = ∫∫(a(x, y, z) dσ ). |
|
Σ |
7. Поток векторного поля
7.1. Определение потока векторного поля
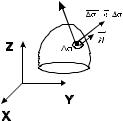
Пусть a = a (P ) - непрерывное векторное поле, а
Σ - ориентированная двусторонняя кусочно-гладкая |
i = |
0 i |
|
Pi i |
|
||
поверхность (имеющая конечное число границ - ли- |
0 |
||
ний излома). |
Разобьем поверхность на n частей |
|
|
Σ1, Σ2 , ..., Σn , |
каждая из которых имеет площадь |
|
|
∆σ1, ∆σ2 , ..., |
∆σn , и выберем точку Pi на каждом из |
|
|
участков Σi . В точке Pi построим единичный вектор нормали n0 (Pi ) к поверхности Σi .
Составим вектор ∆σi = n0 (Pi ) ∆σi с длиной ∆σi , направленный по нормали n0 (Pi ) . Вычислим скалярное произведение (a(Pi ) ∆σi ), просуммируем
по всем участкам ∑n (a(Pi ) ∆σi ) и рассмотрим предел суммы при
i=1
max (∆σi )→0 .
