Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции Соболева часть 3

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

3 Мб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

58 Лекция 5 - 9

Выберем поверхность Σ, охватывающую область G. Из теоремы Остроградского – Гаусса следует, что ∫∫ (a, n0 )dσ =∫∫∫diva dxdydz .

Σ G

Воспользуемся теоремой о среднем, согласно которой существует такая точ-

ка М1, принадлежащая G, что diva \|M1	V = ∫∫adσ ; diva(M1 ) =	∫∫adσ		, где V –
		Σ
			V
	Σ
объем G. Пусть Σ стягивается в	точку М, тогда М1→М,		а diva(M1)

∫∫(a,dσ)

→diva(M ) , diva(M ) = lim	Σ		.
		V
Σ→M

Поскольку правая часть выражения не зависит от системы координат (инвариантна), то инвариантно и данное определение дивергенции.

7.8.1. Физический смысл дивергенции
		∫∫(a, dσ)
Поскольку величина		Σ		имеет смысл средней плотности потока в
Поскольку величина		V		имеет смысл средней плотности потока в
		V				∫∫a, dσ
пространственной области G, то			lim			∫∫a, dσ	= diva есть плотность потока в
						Σ
						V
точке М.			Σ→M			V
точке М.
Точки поля,	в	которых				дивергенция положительна, т.е.
diva(M ) > 0 Π > 0 ,	называют источниками векторного поля, а точки, в
которых дивергенция отрицательна,					diva(M ) < 0 Π < 0 - стоками вектор-
ного поля.

СВекторные линии векторного поля начинаются в точках поля с положительной дивергенцией, а заканчиваются в точках с отрицательной дивергенцией.

О Величину div a(M ) называют мощностью источника или стока.

Теория поля

8. Линейный интеграл в векторном поле

8.1. Понятие линейного интеграла

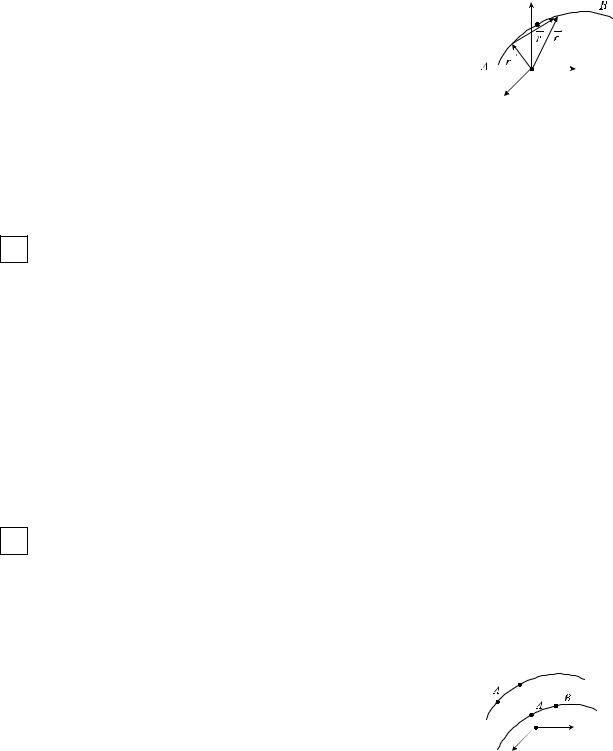
Рассмотрим кусочно-гладкую кривую L и дугу						Z	Ai
AB (обозначение AB )	и	векторное	поле	Ai−1 ∆ i−1
a = (ax ,ay ,az ) , непрерывное	на	L. Разобьем	дугу				i

					i−1
AB произвольным образом точками A0, A1, …An на
							Y
n частей. Обозначим ∆ri - вектор,		стягивающий кон-		X
цы дуги Ai-1Ai . Выберем точку		Pi Ai-1Ai . Най-

дём скалярное произведение (a(Pi ),∆ri ) и просуммируем по всем участкам

дуг S

(a(P),∆r ) . Вычислим предел lim S

lim

(a(P ), ∆r ) .

∑

n→∞

max(

∆r

→0)

i=1

ОЕсли этот предел существует и не зависит от способа разбиения дуги

AB на отдельные участки и от выбора точки Pi, то он называется ли-

нейным интегралом вектора a по дуге AB в направлении от А до В.

Обозначение: ∫ (a,dr ) . Координатная форма записи:

∫ (a,dr ) = ∫ axdx + aydy + az dz =

AB AB

=∫ ax (x, y, z)dx + ay (x, y, z)dy + az (x, y, z)dz ,

				n
∫	(a,dr ) = max	lim∆r	→0	∑(a(Pi ), ∆ri ) .
∫	(a,dr ) = max	lim∆r	→0	∑(a(Pi ), ∆ri ) .
AB			i	i=1
			i

!Линейный интеграл иногда называют криволинейным интегралом второго рода.

8.2. Свойства линейного интеграла

1.Свойство линейности:

∫ ((λa + µb), dr ) = λ ∫ (a,dr ) + µ ∫ (b,dr ) .

2.Свойство аддитивности:

∫ (a,dr ) = ∫ (a,dr ) + ∫ (a, dr ) .

AB AC CB

C Z

60	Лекция 5 - 9

3.При изменении направления интегрирования линейный интеграл меняет

знак: ∫ (a,dr ) = − ∫ (a,dr ) .

Свойства 1-3 доказываются из определения.

!Определение криволинейного интеграла остается справедливым, если начальная и конечная точка совпадают.

О Криволинейный интеграл по замкнутому контуру
называется циркуляцией векторного поля по
замкнутому контуру: C = ∫	(a, dr ) .	+
L

Положительным направлением обхода считается то, при котором область, ограниченная контуром, остается слева.

8.3. Вычисление линейного интеграла

Пусть AB L и кривая L задана параметрическими уравнениями:

		x = x(t)
			= y(t) ,
		L : y	= y(t) ,
			= z(t)
		z	= z(t)
		x = x(t				)	x	= x(t )
при этом при t = t0			0		0		1	1
при этом при t = t0		имеем точку A: y0		= y(t0 ) , при t = t1			B : y1	= y(t1 ) ,
		z	0	= z(t	0	)	z	= z(t	)
			0		0		1	1
тогда
∫ (a,dr ) = ∫ ax (x, y, z)dx + ay (x, y, z)dy + az (x, y, z)dz =
AB	AB
t1		i			i			i

= ∫{ax (x(t), y(t), z(t)) x(t) +ay (x(t), y(t), z(t)) y(t) + az (x(t), y(t), z(t)) z(t)}dt ,

ii i

где точки над символами x, y, z означают дифференцирование по переменной t.

Теория поля

Пример:

Дано:

x = R cos t

=0), B(t1 =2π ).

a = zi + xj + yk , L: y = R sin t , A(t0

z = 2π

Вычислить линейный интеграл по AB .

Решение:

∫(a, dr ) = ∫zdx + xdy + ydz =

2∫π

{

(−R sin t) + R cos tR cos t +

R sin t}dt =

2π

∫sin tdt = πR +R.

2π

8.4. Физический смысл линейного интеграла

Рассмотрим в качестве поля a силу F , приложенную к материальной точке Р и меняющуюся по величине и направлению при изменении местоположения точки Р. A = (F,dr ) - работа по перемещению материальной точки

по участку dr , тогда ∫ (F,dr ) = A - работа силы F по перемещению мате-

риальной точки по дуге АВ.

8.5. Ротор (вихрь) векторного поля

Пусть вектор-функция a = a(P) = (ax ,ay ,az ) является непрерывно дифференцируемой в каждой точке области определения.

ОРотором векторного поля (вектора) a называется вектор, обозначаемый символом rot a , равный

∂a

∂ay

∂a

∂ay

∂a

rota = i

−

+ k

−

x .

∂z

∂x

∂y

∂x

∂z

∂y

Это выражение удобно записать в виде символического определителя

62				Лекция 5 - 9
	i	j	k
rot a =	∂	∂	∂	,
rot a =	∂x	∂y	∂z	,
	∂x	∂y	∂z

ax ay az

который вычисляется разложением по первой строке (базисным векторам i , j,k ); произведение частных производных на компоненты вектора понима-

ется как дифференцирование последних, т.е. ∂∂z ax = ∂∂azx и т.п. С использова-

нием оператора набла rot a = , a или rot a = ×a .

!Если в некоторой точке поля rot a = 0 , то поле в этой точке называется безвихревым.

Пример:

a = (x + z)i + ( y + z) j + (x2 + z)k .

rota =

∂

= i (

∂

(x2 + z) −

∂

( y + z)) −

∂x

∂y

∂z

∂y

∂z

x + z

y + z

x2 + z

−j( ∂∂x (x2 + z) − ∂∂z (x + z)) + k ( ∂∂x ( y + z) − ∂∂y (x + z)) =

=− i − j(2x −1) + 0k = { −1, 1−2x, 0 }.

8.5.1.Свойства ротора (вихря)

1.Линейность: rot(λa + µb) = λ rota + µ rotb , где λ и µ - некоторые постоянные. Иначе, ,(λa + µb) = λ ,a + µ ,b .

2.Пусть u = u(x, y, z) - скалярное поле, тогда rot(u a) =

=[gradu, a]+u rot a .

В векторных обозначениях: [ ,(ua)] =[ u,a] +u[ , a]. Доказательство:

∂

[ ,(ua)] =

(uaz ) −

(uay )

−

(uaz ) −

(uax )

∂x

∂y

∂z

∂y

∂z

∂x

∂z

uax

uay

uaz

Теория поля

∂

= u { i

∂

az −

∂

ay ) − j(

∂

az −

∂

ax ) +k (

∂

(uay ) −

(uax )

(

−

ax ) }+

∂x

∂y

∂z

∂x

∂z

∂x

∂y

+ i (

∂u az −

∂u ay )

+ j(∂u az −

∂u ax ) +k (

∂u ay −

∂u ax ) = u rot(a) +[grad u, a].

∂y

∂z

∂x

∂z

∂x

∂y

Пример:

a = const ,

rot(

a) = [grad

, a] +

rota = [grad

, a] =

×a =

r ×a .

8.6. Теорема Стокса

(устанавливает связь между циркуляцией и ротором)

Циркуляция непрерывно дифференцируемого векторного поля a = axi + ay j + az k по произвольному кусочно-гладкому контуру L вычисляется по формуле

∂a

∂ay

∫axdx + aydy + az dz = ∫∫

∂yz −

cosα +

∂z

∂a

∂ay

∂a

x −

z cos β

−

x cosγ dσ .

∂z

∂x

∂y

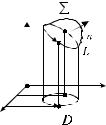
При этом выбор стороны поверхности Σ и направление обхода контура L согласованы (по правилу винта).

Доказательство:

Для доказательства сгруппируем слагаемые в пра-

вой части с одинаковыми координатами вектора a :

∂ax

y1(x)

y2(x)

∫∫(rota, dσ) = ∫∫

cos β −

cosγ dσ +

∂z

∂y

∫∫Σ

∂ay

∫∫Σ

∂a

∂x

∂z

∂y

∂x

cosγ −

cosα dσ

z cosα −

z cos β dσ .

Рассмотрим первый из интегралов:

64 Лекция 5 - 9

∫∫Σ

(

∂ax cos β −

∂ax cosγ )dσ =

∫∫Σ

(

∂ax cos β

−

∂ax )cosγdσ .

∂z

∂y

∂z cosγ

∂y

Пусть

поверхность

однозначно

проектируется на координатную

плоскость Oxy , т.е. любая прямая, параллельная оси Oz , пересекает ее не бо-

лее чем в одной точке; тогда Σ: z = z(x, y) , \| n \|=	∂z 2		∂z 2
лее чем в одной точке; тогда Σ: z = z(x, y) , \| n \|=		+		+1 ;
	∂x		∂y

∂z

, −1

∂x

∂y

cos β = −

∂z ,

так как угол между ортом n

∂z

cosγ

∂y

∂x

(n ,Oz) < π

;

cosγdσ = dxdy .

Переходя

двойному интегралу

∫∫→ ∫∫

, получим

Dxy

D∫∫

∂a (x, y, z) ∂z ∂a (x, y, z)

dxdy .

−

∂z

∂y

−

∂y

и осью

по Dxy:

По формуле дифференцирования сложной функции, записывая полную производную сложной функции, имеем:

			∂ax (x, y, z(x, y)) =			∂ax (x, y, z)		+ ∂ax (x, y, z)			∂z ,
					∂y	∂y				∂z	∂y
			∂a				b	y2 ( x) ∂a		x (x, y, z(x, y))dy =
∫∫ −				x	(x, y, z(x, y))dxdy = −∫dx			∫		x (x, y, z(x, y))dy =
D	xy		∂y				a	y ( x)	∂y
	xy							1
= −∫b ax (x, y2 (x)), z(x, y2 (x))dx + ∫b						ax (x, y1 (x)), z(x, y1 (x))dx == ∫ax (x, y, z)dx .
a					a						L
Докажем последнее преобразование.
			∫ax (x, y, z)dx = ∫ax (x, y, z)dx + ∫ax (x, y, z)dx =…
			L		L1			L2
					{пусть L задана параметрически}…
=		t2 ax (x(t), y(t), z(t)) x(t)t dt +					t1 ax (x(t), y(t), z(t)) x(t)t dt =
		∫t1					∫t2

…{t = x; x(t)t =1}…=

= ∫ab ax (x, y1 (x), z( y1 (x))) dx + ∫ba ax (x, y2 (x), z( y2 (x))) dx .

Остальные два слагаемых рассматриваются аналогично. Почленное суммирование этих выражений приводит к формуле Стокса.

Теория поля

1). Используя обозначение ротора, формулу Стокса можно переписать в ! векторном виде: ∫(a,dr ) = ∫∫(rota, dσ) . Поток вектора rota через

L Σ

ориентированную поверхность Σ равен циркуляции поля a по контуру L, ориентированному в соответствии с ориентацией Σ.

2). Для того чтобы криволинейный интеграл по любому кусочногладкому контуру равнялся нулю, необходимо и достаточно, чтобы выполнялись условия Стокса: ∂∂ayz = ∂∂azy ; ∂∂azx = ∂∂axz ; ∂∂axy = ∂∂ayx .

Пример:

Вычислить циркуляцию вектора	Z
a = yi + x2 j − zk по контуру L:

+ y

= 4;

x = 2cost;

= 2sint; .

z = 3;

= 3.

Решение. Вычислим циркуляцию век-

тора непосредственно:

2π

C = ∫ ydx + x2 dy − zdz = ∫ dt{2sin t(−sin t)2 + 4cos2 t 2cos t −3 0}=

= - 4

2∫πsin 2 tdt +8

2∫πcos2 td sin t = −4

2∫π

1 − cos 2t

dt +8

2∫π(1 −sin 2 t)d sin t =

= −

4t |

2π

+ sin 2t |

2π

+ 8sin t |

2π

− 8

sin 3 t

2π

= −4π ;

C = ∫∫(rota,dσ) = ∫∫(rota, n0 )dσ = ∫∫(rota,(0,0,1))dσ = ∫∫(rota)z dσ =

= ∫∫(−1+ 2x)dσ =…

Вычислим циркуляцию вектора по теореме Стокса: i j k

{rota =

∂

= 0i +0 j +(−1+ 2x)k } = ∫∫(2x −1)dxdy =

∂x

∂y

∂z

Dxy

−z

2∫πdϕ∫2

(2ρ cosϕ −1)ρdρ = ∫2

ρdρ

2∫π(2ρ cosϕ −1)dϕ =

= ∫2

ρ(2ρ sinϕ

02π − 2π )d ρ = −2π

ρ2

= −4π .

66 Лекция 5 - 9

8.7. Инвариантное определение ротора

	i	j	k
Ранее было дано определение ротора rota =	∂	∂	∂	, справедливое
Ранее было дано определение ротора rota =	∂x	∂y	∂z	, справедливое
	∂x	∂y	∂z
	ax	ay	az

лишь в декартовой системе координат.

Теорема Стокса позволяет дать инвариантное (независящее от системы координат) определение ротора векторного поля.

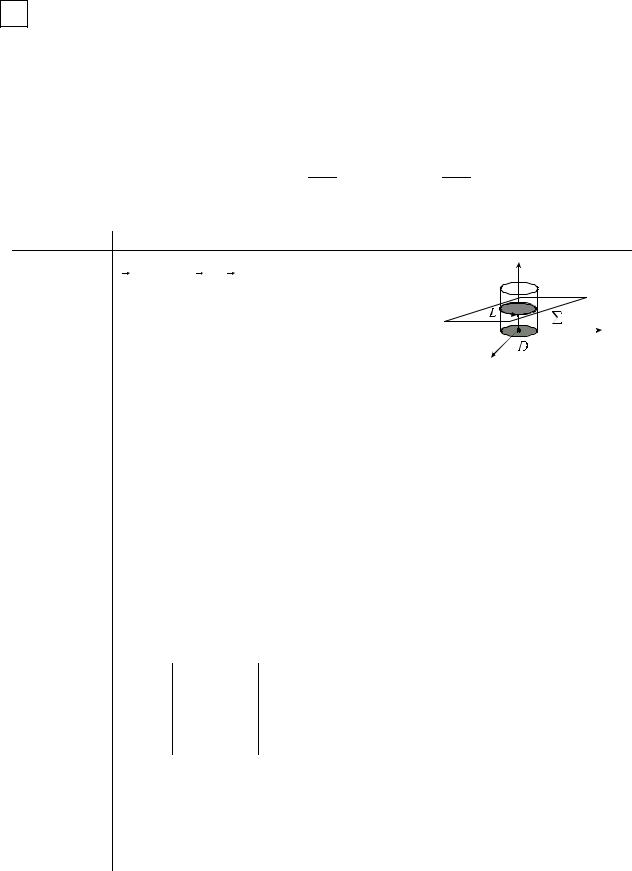
Пусть a = a(P) - векторное поле, удовлетво-	a
ряющее теореме Стокса; n0 - некоторое фиксиро-	no
ванное направление, проходящее через точку М;	M
ванное направление, проходящее через точку М;
D - плоская область величины SD , охватывающая

точку М, а L - граница области D. Направления обхода контура L и ориентация области D согласованы в соответствии с теоремой Стокса:

∫(a,dr ) = ∫∫(rota, dσ) или ∫∫(rota, dσ) = ∫∫Πpn0 rotadσ .

По теореме о среднем существует точка М1: Πpn0 rota(M1) SD = ∫(a, dr ) .

								L
	Πpn rota(M1) =	∫(a, dr )
Тогда			L		. Будем стягивать контур L в точку М, тогда
Тогда					. Будем стягивать контур L в точку М, тогда
	0		SD
	0
точка M1 → M и Πpn			rota(M ) = lim			∫(a, dr )	. Поскольку	∫(a,dr )	- средняя
						L		L
						SD		SD
	0				L→M	SD		SD
	0				L→M
поверхностная плотность циркуляции поля по площади SD, то проекция
rot(a)	на направление n0			не зависит от выбора систем координат и равна по-

верхностной плотности циркуляции вектора a по контуру L, который стягивает площадку, перпендикулярную этому направлению.

8.8. Физический смысл ротора

Пусть вектор a =V (P) задает поле линейных скоростей жидкости, дви-

жущейся вокруг оси Oz, и в точке Р угловая скорость вращения ω =ωk . Тогда

i j k

V (P) =ω × r = 0 0 ω = −ωyi + ωxj, x y z

Теория поля						67
вычислим
		i		j	k
		i		j	k
rotV (P) =		∂		∂	∂		= 0 i + 0 j + (ω +ω)k = 2ωk .
rotV (P) =		∂x		∂y	∂z		= 0 i + 0 j + (ω +ω)k = 2ωk .
		∂x		∂y	∂z
	−ωy		ωx		0

Итак, ротор поля линейных скоростей равен удвоенной угловой скоро-

сти вращения ω бесконечно малого объема, окружающего точку Р, в предположении, что в рассматриваемый момент времени этот объем жидкости внезапно отвердел. Это объясняет название «вихрь» вектора, так как в обычном представлении вихрь связан с интенсивностью вращения движущихся частиц жидкости (турбулентность, водоворот).

8.9. Формула Грина

Пусть в односвязной плоской области D, имеющей границу L, задано

непрерывно	дифференцируемое						векторное поле
∫(axdx + aydy) = ∫∫(		∂ay	−	∂a	x ) dxdy	,	при этом контур

L	D	∂x		∂y

область D оставалась слева. Доказательство:

Рассмотрим формулу Стокса для данного случая:

∫(a,dr ) = ∫∫(rota, dσ) .

a = axi + ay j , тогда

обходится так, чтобы

L1 L2

L = L1 L2 L3

Σ → D :

cos(γ )

=1,

dxdy =

cos(γ )

dσ ; rota =

∂

; откуда следует

∂x

∂y

∂z

∫∫(rota)z dxdy = ∫∫(

∂ay

−

∂a

x )dxdy .

∂x

∂y

Область D может быть и неодносвязной. В этом случае под линейным интегралом понимается сумма по всем компонентам границы D.

!В некоторых случаях формула Грина позволяет упростить вычисление циркуляции векторного поля.

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.2019861 Кб136Лекции РИМ сводная_1.doc
#
17.11.2019236 Кб13Лекции РЦБ - кусочки.doc
#
21.12.2018682 Кб62Лекции сенсоры.doc
#
24.08.2019643 Кб54Лекции сенсоры.doc
#
23.02.2015732 Кб18лекции сист эл снабж.pdf
#
23.02.20153 Мб81Лекции Соболева часть 3.pdf
#
22.02.20151 Мб377Лекции соц психология.doc
#
23.02.20155 Мб111Лекции Стечкина по матану.pdf
#
01.05.20252 Мб5Лекции ТОМ 7.12.07doc.doc
#
21.12.201816 Мб64Лекции ТЭПП.doc
#
01.04.20253 Мб6ЛЕКЦИИ УПРАВЛЕНИЕ ДАННЫМИ 2012.doc