Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции Соболева часть 3

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

3.38 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 149 10 11 12 13 14 > Следующая >>>

Лекции 10 - 11

тогда

Sn =1

−

+... +

−

=1−

n +1

2 3 3

lim Sn

, ряд сходится по определению.

n→∞

Пример:

∞

1. ∑n = ∞ , ряд расходится.

n=1

∞

= −1, S2 = 0, S3 = −1, S4 = 0,…

2. ∑(−1)n = −1 +1 −1 +1 −…

n=1

Предел частичных сумм не существует, ряд расходится.

∞

3. ∑qn−1 =1+ q + q2 +… По формуле суммы геометрической про-

n=1

b1 (1−qn )

грессии S

, для b

=1 получаем S

1 − qn

1−q

− q

1). Если

<1,

то qn →0 и lim S

= S .

n→∞

1 − q

2).

Если

>1,

то, qn →∞ S

→ ∞ предел S

не существу-

ет.

n→∞

3).

Если q =1, то Sn = n , lim Sn

= ∞ .

n→∞

0, при n четном,

Если q = −1 , то Sn = и предел не существует.

1, при n нечетном

∞	сходится при	q	<1;

Итак, ∑qn−1				q	≥1.

n=1	расходится при

ТОтбрасывание конечного числа начальных членов ряда не влияет на его сходимость (но влияет на сумму).

Доказательство:

Рассмотрим ряды:

∞
∑un = u1 + u2 +…+ un +…	(1)
n=1
∞
∑un = um+1 + um+2 +…	(2)

n=m+1

Обозначим сумму отброшенных членов через А. Тогда частичная

сумма для ряда (1)	при n>m равна Sn = A +δn−m , где δn−m - частич-
ная сумма ряда (2).

Числовые ряды

При n → ∞ : (n − m) = k → ∞ , lim Sn = A + limδk .

Так как существу-

ет lim A = A , то Sn и δk

n→∞

k→∞

сходятся или расходятся одновременно (по

n→∞

теореме о пределе суммы).

∞

Если члены сходящегося ряда ∑un = S

умножить на одно и то же

n=1

число С, то его сходимость не нарушится, а сумма умножится на

∞

это число: ∑Cun =CS .

n=1

=C lim Sn =CS .

Доказательство: limCSn

n→∞

Пример:

∞

Sn = a −aq

Ряд ∑aqn−1 сходится при

<1.

, S =

n=1

1−q

−q

∞

Два сходящихся ряда ∑an = A и ∑bn

= B можно почленно склады-

n=1

∞

вать (вычитать) так, что ряд ∑(an ± bn )

- сходится, и его сумма

равна A ± B .

n=1

Доказательство:

Sn = (a1 ± b1 ) + (a2 ± b2 ) +…+ (an ± bn ) =

= (a1 + a2 +…) + (b1 + b2 +…) = An ± Bn ;

lim S

= lim A ±lim B = A ± B.

n→∞

n→∞ n

n→∞

ТКритерий Коши сходимости числового ряда. Для того чтобы число-

вой ряд был сходящимся, необходимо и достаточно, чтобы для

ε > 0, N = N (ε), n > N

и k = 1,2,3,…

выполнялось неравенство

Sn+k − Sn

un+1 +un+2 +…+un+k

< ε .

Необходимый

признак

сходимости числового ряда. Если ряд

∞

∑un сходится,

то общий член сходящегося ряда стремится к нулю

n=1

при n → ∞ , lim un = 0.

n→∞

Доказательство:

un = Sn − Sn−1. Так как lim Sn = lim Sn−1 = S, то

lim un = 0. В противном

n→∞

случае ряд расходится.

80 Лекции 10 - 11

Это условие не является достаточным.

∞

Покажем, что гармонический ряд ∑

=1 +

+…+

+… расхо-

n=1 n

дится, несмотря на то, что lim u

= lim

= 0.

n→∞

n→∞ n

Рассмотрим

S2n − Sn = n1+1 + n +1 2 +…+ 21n > 21n + 21n +…+ 21n = n 21n = 12 .

Таким образом, критерий Коши не выполняется и гармонический

∞	1n расходится.
ряд ∑n=1

Пример:

∞	4	−5n	2
1. Исследуйте на сходимость ряд ∑				.
	(n −	1)(n +2)
n=1

Ряд расходится, так как для него не выполняется необходимый признак сходимости:


lim u	n	= lim	4 −5n2	= lim	4 −5n2				= −5	≠ 0
lim u		= lim	(n −1)(n + 2)	= lim		+ n −		2	= −5	≠ 0
n→∞		n→∞	(n −1)(n + 2)	n→∞ n2		+ n −		2
				∞ n			n
2. Исследуйте на сходимость ряд ∑							.
2. Исследуйте на сходимость ряд ∑							.
				n=1 n +		1

Проверим выполнение необходимого признака сходимости:

lim u

= lim

;

l ≠

n→∞

n→∞ n +1

n→∞

ряд расходится.

Числовые ряды

10.2. Ряды с положительными членами

∞

Рассмотрим числовой ряд ∑un =u1 +u2 +…+un +…, где un ≥ 0,

n=1

n =1,2,3,….. Для такого ряда Sn+1 = Sn +un+1 ≥ Sn , значит, последователь-

ность частичных сумм возрастает. Из теоремы о пределе монотонной последовательности вытекает следующее.

Условие сходимости ряда с положительными членами: ряд с по-

ложительными членами всегда имеет сумму; она будет конечна (а ряд сходящимся), если частичные суммы ряда ограничены сверху, и бесконечна (а ряд расходящимся) в противном случае.

10.3. Теоремы сравнения рядов с положительными членами

Пусть даны два положительных ряда:

∞
∑un , un ≥ 0	(1)
n=1
и
∞
∑vn , vn ≥ 0 .	(2)

n=1

ТЕсли хотя бы начиная с некоторого n выполняется неравенство

un ≤ vn , то из сходимости ряда (2) следует сходимость ряда (1); из

расходимости ряда (1) следует расходимость ряда (2). Доказательство:

Так как отбрасывание конечного числа начальных членов ряда не

влияет на сходимость, можно считать, что un ≤ vn		n =1, 2, 3, ….
Для частичных сумм этих рядов выполняется Un ≤Vn .
∞		∞
Пусть ряд ∑vn сходится, тогда Vn ≤ S, откуда Un ≤ S и ряд ∑un схо-
n=1		n=1
дится.
∞		∞
Пусть ∑un расходится, тогда Un	≥ S , Vn ≥ S и ряд	∑vn расходится.
n=1		n=1

ТЕсли существует конечный предел отношения общих членов (1) и

(2)	lim	un	= k , vn ≠ 0, 0 ≤ k < ∞, то оба ряда либо одновременно схо-

	n→∞ vn

дятся, либо одновременно расходятся.

Лекции 10 - 11

Пример:

Исследуйте на сходимость следующие ряды:

∞

=1 +

1 +…+

1 +…

1) ∑

n=1

Сравним члены этого ряда с членами расходящегося гармониче-

∞

1 .

. Так как

1 ,исследуемый ряд расходится.

ского ряда ∑

≥

n=1

∞

2) Ряд ∑

сходится по теореме сравнения, так как предел отно-

n=1 n

шения общего члена данного ряда к общему члену сходящегося

∞

n(n +1)

(доказано

ранее)

ряда ∑

есть

lim

=1, постоянное

n(n +1)

n=1

n→∞

(n +1)

число.

∞

3) ∑

=1 +

+…+…

+… .

n=1

∞

Сравним этот ряд с рядом

∑

…+

+…, который

n=1

представляет собой бесконечно убывающую геометрическую про-

грессию со знаменателем q =

<1, а следовательно, сходится.

Так как

, исследуемый ряд сходится.

∞

4) Ряд ∑ln 1

∑un .

n=1

∞

Сравним этот ряд с расходящимся рядом ∑

n=1

ln(1 +

)

что (ln(1+α) ~ α) .

lim

= lim

=1, с учетом того,

n→∞ vn

n→∞

n→∞ 1n

Приведем полученные данные о сходимости некоторых рядов, ко-

торые могут быть использованы для сравнения:

∞

сходится, еслиα >1,

∑

n=1

расходится, еслиα ≤1.

∞

сходится, если

<1,

∑

≥1.

т=1

расходится, если

∞

∑

сходится.

т=1 n(n +1)

∞

сходится при

<1,

∑aq

≥1.

−q

n=0

расходится при

Числовые ряды

11.1.Достаточные признаки сходимости числовых рядов

сположительными членами

11.1.1. Признак Даламбера

∞

Рассмотрим ряд

∑un с положительными членами и предел отно-

n=1

шения последующего члена ряда к предыдущему.

1) Если un > 0; и 2) существует lim

un+1

= l,

тогда

n→∞ un

сходится, еслиl <1,

∞

расходится, еслиl >1,

∑un

n=1

признакнедаетответа, еслиl =1.

Доказательство:

un+1

т.е. l −ε <

un+1

< l +ε.

lim

= l ε > 0

N : n ≥ N,

−l

< ε,

n→∞

Рассмотрим 3 случая:

1)l <1.

Выберем ε	столь малым, чтобы l +ε <1, тогда, полагая l +ε = q,
0 < q <1, имеем	un+1 < q, un+1 <un q для n = N, N +1, N + 2,…,uN +1 <uN q,
	un

uN +2 < uN +1 q < uN q2 , uN +3 < uN +2 q < uN q3 и т.д.

Члены ряда uN +1 +uN +2 +uN +3 +…(1) меньше членов геометрической прогрессии: uN q +uN q2 + uN q3 +…(2). Так как q <1, то ряд (2) сходится, значит, по теореме сравнения сходится и ряд (1).

2)	l >1.	un+1 >1,
Возьмем ε > 0 столь малым, что l −ε >1, тогда при n ≥ N		un+1 >1,
		un

un+1 >un , члены ряда не стремятся к нулю, т.е. не выполняется необходимый признак сходимости ряда, следовательно, ряд расходится.

3)l =1.

Покажем, что в этом случае ряд может как сходиться, так и расходиться.

1). Гармонический ряд	∞ 1	расходится, для него lim un+1	= lim	n	=1.

	∑n=1 n

		n→∞ un	n→∞ n +1

Лекции 10 - 11

∞

un+1

2). Рассмотрим ряд ∑

Для него также lim

= lim

=1. Срав-

n=1

n→∞

n→∞ (n +1)

∞

ним члены исследуемого ряда со сходящимся рядом ∑

(доказа-

n(n +

n=1

∞

но ранее): ∑

= ∑

, значит,

∑

сходится.

(n +1)

n(n +1)

(n +

n=1

n=0

n=1

Пример:

Исследуйте на сходимость ряды:

∞

1) ∑

un =

un+1 =

1 2 3…n

(n +1)!

2 3…n(n +1)

n=1 n!

lim

un+1

= lim

= 0 .

n→∞ un

n→∞ n +1

Ряд сходится.

∞

∑2n +1.

n=1

n2n

un+1

+ 3

Вычислим lim

= lim

<1,

n+1

n→∞ un

n→∞ 2n +1 n +1

2 2

ряд сходится.

∞

∑

n!(2n +1)!

можно убедиться, что un → 0.

n=1

(3n)!

Вычислим lim

(n +1)!(2(n +1) +1)!(3n)!

= lim

(n +1)!(2n +3)!(3)!

(3n + 3)!n!(2n +1)!

(3n +3)!n!(2n +1)!

n→∞

lim

(n +1)(2n + 2)(2n + 3)

. <1, исследуемый ряд схо-

(3n + 3)(3n + 2)(3n +1)

n→∞

дится.

11.1.2. Признак Коши

Если 1) un	> 0 и 2) существует lim n un = l,
тогда	n→∞
тогда

∞	сходится, еслиl <1,
∞	расходится, еслиl >1,
∑un	расходится, еслиl >1,
n=1
	признакнедаетответа, еслиl =1.
Доказательство:

lim n un = l ε > 0 N : n > N		n un −l	< ε, l −ε < n un −l < l +ε.
n→∞
n→∞

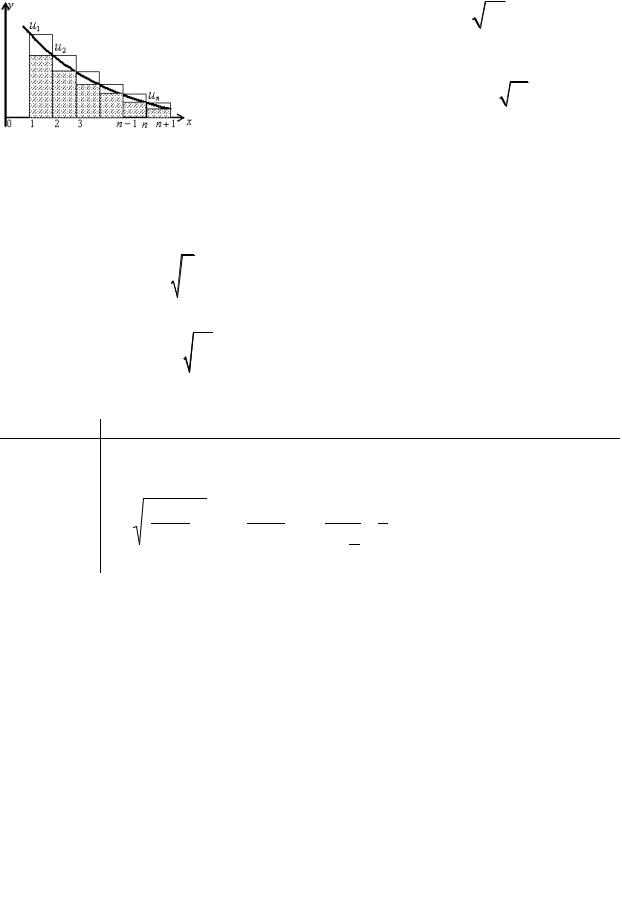
Числовые ряды

l <1. Выберем ε

так, чтобы l +ε = q,

q <1.

Тогда n un < q, un < qn .

∞

Так как ∑qn сходится при q <1, то и ∑un - сходится.

n=1

>1. Выберем ε

так, чтобы q = l −ε >1. Тогда l −ε > n un

> qn >1: limu

≠ 0 и

∞

расходится при l >1.

∑

n→∞

n=1

l =1. Признак ответа не дает, ряд может как сходиться,

так и рас-

ходиться.

Рассмотрим те же примеры, что и при рассмотрении признака

Даламбера.

∞

ln n

∑

. Пусть

= C

n ,

ln C

= −

→0

= →1

n→∞

n=1

но ряд расходится.

∞

∑

′

′ = −

2 ln n

→

C′ = →1

2 . Пусть

0 ,

, ln Cn

n→∞

n=1

но ряд сходится.

Пример:

∞	n	n
Исследуйте на сходимость ряд ∑		.
Исследуйте на сходимость ряд ∑	2n +1	.
n=1	2n +1

	n	n	= lim	n	= lim		1	=	1	<1, ряд сходится.
lim n	2n +1		= lim	2n +1	= lim		1	=	2	<1, ряд сходится.
n→∞	2n +1		n→∞	2n +1	n→∞		1		2
						2	+ n

11.1.3. Интегральный признак сходимости

Пусть 1) un > 0 и 2) un ≥ un+1 не возрастают, 3) f (n) − непрерывная не возрастающая функция такая, что f (n) = un .

∞

Тогда ряд ∑un и несобственный инте-

n=1

грал ∞∫ f (x)dx либо одновременно сходятся,

либо одновременно расходятся. Доказательство:

Изобразим ситуацию геометрически. Площадь криволинейной трапеции, ограниченной прямыми x =1, x = n +1 , y = 0 и

86	Лекции 10 - 11

графиком функции y = f (x), равна In+1 = n∫+1 f (x)dx .

Площадь ступенчатой фигуры, описанной около этой криволинейной трапеции, равна частичной сумме ряда Sn = u1 +u2 +…+un .

Площадь ступенчатой фигуры, вписанной в ту же криволинейную трапецию, равна Sn+1 −u1 =u2 +u3 +…+un+1 .

Последовательность частичных сумм {Sn } и последовательность

{In } монотонно возрастают: Sn+1 − Sn = nn+1 > 0 , In+1 − In = n∫+1	f (x)dx > 0.
n

Очевидно, Sn+1 −u1 < In+1 < Sn .

Переходя к пределам, получаем lim S

n+1

−u ≤ lim I

n+1

n→∞

как lim S

n+1

= lim S

и lim I

n+1

= lim I

, то lim S

−u

≤ lim I

≤

n→∞

∞

1).

Если

интеграл

сходится,

lim I

= I =

∫

n→∞

≤ lim Sn , или, так

n→∞

lim Sn .

n→∞

f (x)dx < ∞ ,

то

lim Sn ≤ I +u1 < ∞,

ряд

сходится.

Если

ряд

сходится,

lim S

= S <∞,

то

n→∞

lim In ≤ S < ∞ , интеграл сходится.

n→∞

2).

Если интеграл расходится, I

→∞,

то и

→∞ (так

n→∞

как

> I

), ряд

расходится.

Если

ряд

расходится,

→∞,

то

n→∞

−u

) →∞,

и,

так как I

> S

−u ,

→∞,

интеграл расходит-

n→∞

ся.

Пример:

Исследуйте на сходимость ряды:

∞

; f (x) =

1) ∑

(n +1) ln

(x +1) ln

(x +

n=1

(n +1)

∞

d(ln(x +1))

= lim −

∫(x +1) ln 2 (x +1)

∫

ln 2 (x +1)

ln(x +1)

a→∞

−

= lim

ln 2

a→∞ ln 2

ln(a +1)

исследуемый ряд сходится.

∞

2) ∑

= ∑un .

(n − 2) ln(n −3)

n=5

Исследуем на сходимость вспомогательный ряд

∞

∑

= ∑vn

ln(n −3)

n=5 (n −3)

с помощью интегрального признака.

Числовые ряды

∞

Несобственный интеграл ∫

= ∫

= 2 ln(x −3)

= ∞

5 (n −3)

ln(x −3)

расходится, следовательно, расходится вспомогательный ряд

∞

∑vn .

n=5

Так как lim

= lim

n −3

=1, то по второй теореме сравнения ис-

n→∞ vn

n→∞ n − 2

ходный ряд также расходится.

∞

3) ∑

; f (x) =

n=1 n

∞

dx = lim ln

a = ∞, исследуемый ряд расходится.

∫1 x

a→∞

Заметим, что для оценки остатка ряда Rn с положительными чле-

нами удобно пользоваться интегральным признаком сходимости.

∞

Если этот признак применим к ряду ∑ f (n), то имеет место оценка

n=1

∞∫ f (x)dx < Rn < ∞∫ f (x)dx .

n+1

Пример:

∞

Сколько членов ряда ∑

нужно взять, чтобы получить значение

n=1

суммы ряда с точностью до 0,001?

Здесь f (x) =

∞∫

= −

∞ =

, по условию

> 0,001, n >1000, зна-

n x

чит нужно взять 1001 член.

11.2. Знакопеременные ряды

Т Если для знакопеременного ряда
∞
∑un = u1 +u2 +…+un +…	(1)

n=1

сходится ряд, составленный из абсолютных величин его членов,

∞
∑un = u1 + u2 +…+ un +…,	(2)

n=1

то ряд (1) сходится. Доказательство:

Рассмотрим вспомогательный ряд

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 149 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.2019861.18 Кб52Лекции РИМ сводная_1.doc
#
17.11.2019235.52 Кб5Лекции РЦБ - кусочки.doc
#
21.12.2018681.98 Кб40Лекции сенсоры.doc
#
24.08.2019642.56 Кб28Лекции сенсоры.doc
#
23.02.2015732.41 Кб11лекции сист эл снабж.pdf
#
23.02.20153.38 Mб58Лекции Соболева часть 3.pdf
#
22.02.20151.15 Mб282Лекции соц психология.doc
#
23.02.20154.81 Mб90Лекции Стечкина по матану.pdf
#
21.12.201816.1 Mб40Лекции ТЭПП.doc
#
31.08.2019196.83 Кб7Лекции Философия.docx
#
20.09.20191.05 Mб13лекции ЦБ.docx