Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции Соболева часть 3

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

3.38 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

68	Лекция 5 - 9

Пример:

Вычислить циркуляцию вектора

a = 1+ x2 + y2 i + y[ xy +ln( x + 1+ x2 + y2 )] j

по контуру L: x2 + y2 = R2.

Тогда: C= ∫

1 + x 2

+ y 2 dx + y xy + ln

(x +

1 + x

2 + y

2 ) dy .

Вычислим циркуляцию по формуле Грина:

y 1

∂ax

∂ay

1 + x

+ y

= y

∂y

1 + x2 + y 2

∂x

x + 1 + x2

+ y 2

= y

+ y

( 1 + x2 + y2 + x)

= y

1 + x2 + y2 (x + 1 + x2 + y2 )

1 + x2 + y 2

∫∫

∂ay

∂a

∫

∫∫

С=

(a, dr ) =

−

dxdy

y2 +

−

dxdy =

Dxy ∂x

∂y

Dxy

1+ x + y

= ∫∫ y

2dxdy = ∫

d ϕ

2π

∫ ρ d ρ ( ρ 2 s in 2 ϕ ) =

∫1 − cos2

2ϕ dϕ∫ρ3dρ =

2 π

Dxy

2π

sin 2ϕ

2π

πR4

ϕ |0

−

2π

9. Специальные виды векторных полей

9.1. Потенциальное векторное поле

О Векторное поле a называется потенциальным, если оно является градиентом некоторого скалярного поля (функции) u = u(P) , т.е.

a = grad (u) . Это векторное равенство равносильно трем скалярным:

(x, y, z) =

∂u(x, y, z)

; a

∂u

; a

∂u

. Иначе:

du = a

dx + a

dy + a

dz .

∂x

∂y

∂z

Функция u в этом случае называется силовой функцией, или потен-

циалом поля.

!Потенциал u определяется с точностью до постоянного слагаемого.

Теория поля

Пример:

Показать, что поле a =

r потенциально.

r 3

Рассмотрим функцию u

= − e ;

∂u

∂

(1) = e

∂

= −e

x2 + y2 + z2 = = e

(

) = e

;

∂x

r2 ∂x

+ y2 + z2

∂x r

∂u

= e

;

∂u

= +e

grad (u) = +

r ;

a = grad (u) u - потенциал

∂y

∂z

поля a .

9.1.1. Условия потенциальности поля

1.Циркуляция векторного поля по любому замкнутому контуру, лежащему

вобласти непрерывности потенциального поля, равна нулю. Доказательство:

Рассмотрим

∂

rot(grad(u)) =

∂

−

j +

∂x

∂y

∂z

∂y∂z

∂x∂z

∂z∂y

∂z∂x

∂

∂x

∂y

∂z

∂

k = 0 rota = 0.

−

∂x∂y

∂y∂x

По теореме Стокса ∫(a,dr ) = ∫∫(rota, dσ) = 0 .

LΣ

2.Линейный интеграл в потенциальном поле не зависит от пути интегрирования и равен разности потенциалов поля в конечной и начальной точках интегрирования.

Доказательство:

Так как поле потенциально: a = grad (u) = ∂u i +

∂u

j + ∂u k

∂x

∂y

∂z

∫ (a,dr ) = ∫ axdx + aydy + az dz = ∫

∂u

dx +

∂u

dy +

∂u

∂x

∂y

∂z

∂u

x(t) +

∂u

y(t) +

∂u

= ∫dt

∂y

∂z

z(t)

= ∫

dt = ∫du =

∂x

= u(x(t), y(t), z(t)) |tB = u(x(t

), y(t

), z(t

)

-u(x(t

), y(t

), z(t

)) = u(B) −u( A) .

70	Лекция 5 - 9

Т(Условие 3) Для того чтобы векторное поле a = a(P) в некоторой односвязной области G было потенциальным, необходимо и достаточно, чтобы оно было безвихревым, т.е. rot(a) = 0 .

Доказательство:

Необходимость.

Пустьa = a(P) - потенциальное поле a = grad (u)

rota = rot(grad(u)) = 0 .

Достаточность.

В силу свойства 2, если зафиксировать начальную точку А(0,0,0), криволинейный интеграл станет некоторой функцией пе-

ременной точки P(x,y,z): u(P) = ∫ (a,dr ) .

A(x0 ,y0 ,z0 ) P(x,y,z)

P1(x,y0 ,y0 ) P2(x,y,y0 )

Вычислим производную функции u(P) в точке P по направлению PP'. При переходе

от точки P к точке P' функция u получит приращение

∆u = ∫ (a,dr ) =	∫ ΠpPP 'adl = ΠpPP 'a(P1) ∆l , где P1 PP ' по теореме о
PP '	PP '
среднем. Следовательно, ∆u = Πp			PP '	a(P ) . Переходя к пределу при
	∆l				1
		∆u =	∂u
P → A и ∆l → 0 , имеем lim					= ΠpAP a( A) . Поскольку производ-
	∆l →0	∆l	∂l

ная поля ∂∂ul по направлению AP равняется проекции grad(u) на это направление, то a = grad (u) .

!Условие 3 часто используют в качестве критерия потенциальности векторного поля.

9.1.2. Вычисление потенциала поля

Потенциал векторного поля по условию 2 может быть найден по формуле

u = ∫ axdx + aydy + az dz , где А (x0, y0, z0) - фиксиро-

ванная точка поля, координаты которой удовлетво-

ряют условиям существования полей a и rota ( как правило, А(0,0,0)), а Р(x,y,z) - текущая точка поля. Линейный интеграл вычисляется по любому контуру дуги L : AP . Наиболее удобен для вычисления контур в виде ломаной, звенья которой параллельны осям координат.

P(x,y,z)

A(0,0,0)

P1(x,0,0) P2(x,y,0)

Теория поля

В этом случае

x y z

u(x, y, z) = ∫ax (x, y0 , z0 )dx +∫ay (x, y, z0 )dy +∫az (x, y, z)dy .

x0 y0 z0

Пример:

Доказать, что поле a = x2i + y2 j + z2k является потенциальным,

и найти его потенциал.

Решение: Используя критерий потенциальности поля (условие 3), имеем: rot(a) = 0 a - потенциальное поле.

u = ∫(a, dr ) =

∫

x2dx + y2dy + z2dz =

∫

... + ∫

... +

∫ ...

AP1

P1P2

P2 P

AP1 : z = 0 dz = 0; y = 0 dy = 0;

P1P2 : x = const dx = 0; z = 0 ;

P2 P : x = const dx = 0; y = const dy = 0

x3 + y3

+ z

u = ∫x

x2dx + ∫y2dy + ∫z

z2dz =

+c .

x3 + y3

+ z3

3x2

3z 2

Проверка: gradu = grad (

) =

j +

k = x

i + y

j + z

k .

9.2. Соленоидальное поле

ОВекторное поле a = a(P) называется соленоидальным (трубчатым), если в каждой точке P заданного поля div(a) = 0 .

9.2.1. Свойства соленоидального поля

1.Соленоидальные поля не имеют источников и стоков, что следует из определения.

2.Поток a через любую замкнутую ориентированную кусочно–гладкую поверхность, лежащую в поле равен нулю:

П = ∫∫(a dσ) = ∫∫∫diva dV = 0 .

Σ G

3.В соленоидальном поле векторные линии не могут начинаться или кончаться во внутренней точке области; они либо замкнуты, либо начинаются и кончаются на границе поля.

4.Поток векторного поля через поперечное сечение векторной трубки в соленоидальном поле остаётся постоянным вдоль всей трубки.

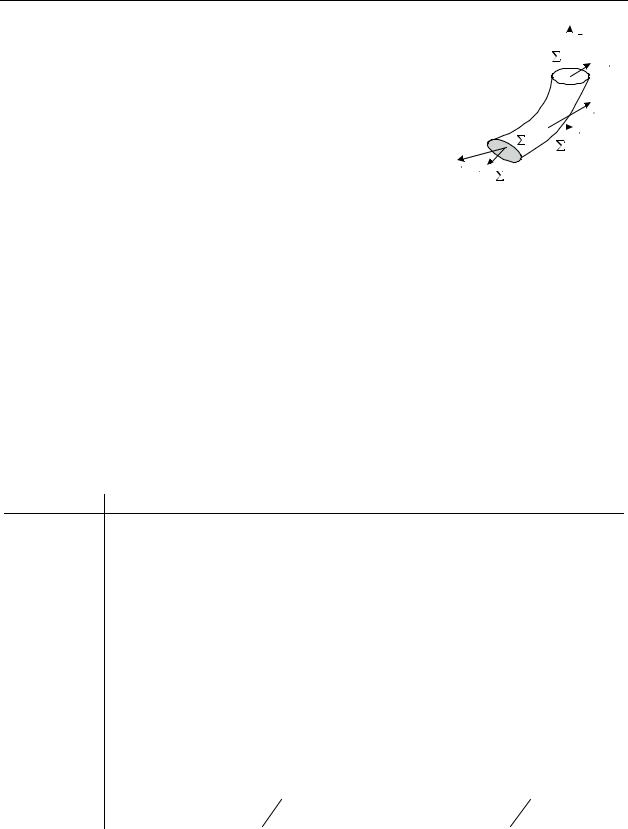
72 Лекция 5 - 9

Доказательство свойства 4:						a
Доказательство свойства 4:						a
Рассмотрим область специального вида -					1
векторную трубку Т ограниченную двумя						n0
векторную трубку Т ограниченную двумя
поперечными сечениями Σ1, Σ2 и боковой по-
верхностью Σ3.						a
Вычислим поток	через	указанную	поверх-	−	3	n0
				−		n0
				2
ность.			a	+
Π = ΠΣ1 + ΠΣ2	+ ΠΣ3		a	n0 2
Π = ΠΣ1 + ΠΣ2	+ ΠΣ3	= ∫∫∫diva dV = 0
(по свойству 2);		T
(по свойству 2);
ΠΣ3 = Π боковой поверхности = ∫∫(a dσ) = ∫∫(a n0 )dσ = 0 ,				так как на поверх-
		Σ3	Σ3
ности векторной трубки Σ3 вектор			a направлен по касательной к по-
верхности, т.е. (a n0 )Σ3		(a n0 )Σ3 = 0 .
Таким образом,
ΠΣ1 + ΠΣ2 = 0 , ΠΣ1 = −ΠΣ2 , ∫∫(a,dσ) = −∫∫(a, dσ) = ∫∫(a, dσ) .
		Σ1	Σ2 +	Σ2 −

Если придать векторному полю смысл скорости течения жидкости, то количество жидкости, вытекающей из поперечного сечения векторной трубки, всегда равняется количеству жидкости, втекающей в нее.

Пример:

1). Является ли соленоидальным поле: a = y2i −(x2 + y2 ) j + z(3y2 +1)k ?

Решение:

diva = −2 y +3y2 +1 ≠ 0

a - не соленоидально.

2). При каком условии векторное поле

a =ϕ(r) r будет соленоидаль-

ным?

Решение:

′

diva = div[ϕ(r)r ] =ϕ(r)divr + (gradϕ(r) r ) = 3ϕ(r) +ϕ (r)

′

(r)

3ϕ(r) +

= 3ϕ(r) +ϕ (r)r

dϕ

′

или 3ϕ(r) = −rϕ (r) ,

rϕ (r) = −3ϕ(r) ,

ϕ = −3

r ,

lnϕ = ln c − 3ln r ; ϕ = c

3 - поле соленоидально, еслиϕ = c

3 .

Теория поля

9.3. Операторы Гамильтона и Лапласа

9.3.1. Оператор Гамильтона (набла)

Многие операции векторного анализа могут быть записаны в сокращенной и удобной для расчётов форме с помощью символического оператора

Гамильтона «набла»: =i

∂

+ j

∂

+ k

∂

;

∂

;

∂

∂x

∂y

∂z

∂x

∂y

∂z

Выражение вида u(x, y, z) понимается как результат действия оператора на соответствующую функцию. Тогда

∂

∂u

k =u′x i +u′y j + u′z k ,

u(x, y,z) = i

+ j

u(x, y,z) =

∂x

i +

∂y

j +

∂z

∂x

∂y

∂z

gradu = u .

В этом операторе соединены дифференциальные и векторные свойства, поэтому при действиях с ним необходимо пользоваться правилами векторной алгебры и дифференцирования.

Выполняя действия с оператором «набла», удобно использовать так называемый символический метод, основанный на применении следующих правил:

1.Если оператор действует на какое-либо произведение, то вначале используются его дифференциальные, а затем векторные свойства.

2.Чтобы отметить тот факт, что «набла» не воздействует на какую-либо величину, входящую в состав сложной формулы, эту величину помечают индексом c (const).

3.Все величины, на которые оператор «набла» не действует, в окончательном варианте ставятся впереди него.

Пример:

Используя символический метод, вычислить div a ×b .

Решение:

Воспользуемся свойствами смешанного произведения:

div a ×b = a ×b = a ×bc + ac ×b = b ×a −a ×b =

= b rot(a) −a rot(b) .

74	Лекция 5 - 9

9.3.2. Оператор Лапласа

Дифференциальные операции второго порядка возникают в результате двукратного применения к полям оператора «набла».

Если в области G задано скалярное поле u = u(P) , то операция взятия градиента порождает векторное поле: grad (u) . В векторном полеu = grad (u) операция взятия дивергенции порождает скалярное поле: ( u) = div(grad (u)) , а операция взятия ротора - векторное поле

×u = rot(grad (u)) .

Если в области G задано векторное поле a = a(P) , то операция взятия

дивергенции порождает скалярное поле: div(a) = ( a) .		В скалярном поле
div(a) = ( a) операция взятия градиента	порождает	векторное поле:
( a) = grad (diva) .
Если в области G задано векторное поле	a = a(P) , то операция взятия

ротора порождает векторное поле rot(a) . Применяя повторно к этому полю оператор , получим скалярное поле div(rot(a)) = ( ×a )и векторное поле rot(rot(a)) = × ×a .

При помощи оператора Гамильтона основные понятия теории поля можно записать в виде операций векторной алгебры.

Рассмотрим некоторые операции второго порядка.

1.Вихревое поле является соленоидальным: div(rot(a)) = 0 .

Раскроем смешанное произведение, учитывая, что векторное произведение одинаковых векторов равно нулю: ×a =a × = a 0 =0.

2. Векторное	поле a = grad (u)	является		безвихревым, так как
rot(grad(u)) = 0. Действительно, ×u			= × u =0 u =0.

3.Рассмотрим операцию div(grad (u)) .

∂u

i +

∂u

j +

∂u

∂2u

=∆u .

div(grad (u)) = ( u) = div

∂x

∂y

∂z

∂x

∂y

∂z

Теория поля									75
	Дифференциальный оператор вида ∆ =		∂2			∂2		∂2
			∂2			∂2		∂2
О			∂x2 +			∂y2 +		∂z2 называется опера-

	тором Лапласа. Оператор Лапласа можно представить как скалярное

	произведение оператора Гамильтона самого на себя:
	∆ = ( ) = = ( )2 =		∂2	+		∂2	+	∂2	.
	∆ = ( ) = = ( )2 =	∂x2		+	∂y2		+	∂z2	.
		∂x2			∂y2			∂z2

Уравнение вида ∆u = 0 называется уравнением Лапласа и является одним из основных уравнений математической физики. Непрерывное решение уравнения Лапласа u(x, y, z) называется гармонической функцией. Соответствующее скалярное поле называется гармоническим или лапласовым.

!Векторное поле является гармоническим, если оно является одновременно потенциальным и соленоидальным: rota = 0 ; diva = 0 .

!Рассмотрим операцию rot(rot(a)) .

Формула

двойного

векторного

произведения

дает:

{формула

«бац минус цаб»}.

Тогда

a × b ×c = b (a c )−c (a b )

(

)

−a

(

)

diva − 2a = grad (diva) − ∆a .

× ×a =

Дифференциальные операции второго порядка удобно свести в таблицу.

	Скалярное поле		Векторное поле
	grad	div		rot

grad		grad(diva)

div	div(grad(u)) = ∆u			div(rot(a)) = 0

rot	rot(grad (u)) = 0			rot(rot(a)) =
rot	rot(grad (u)) = 0			grad (diva) − ∆a
				grad (diva) − ∆a

Пример:

Законы электромагнетизма описываются уравнениями Максвелла в дифференциальной форме:

ε ∂E

= ×H

, −

µ ∂H

= ×E

(

)

= 0 ;

(

)

= 0.

c ∂t

Иначе:

ε ∂E

= rotH

(1),

divE = 0

(2);

−

µ ∂H

= rotE

(3),

divH = 0 (4).

c ∂t

76	Лекция 5 - 9

В данном случае нет зарядов и токов, а E , H - векторы напряжённости электрического и магнитного полей; ε , µ - электрическая и магнитная про-

ницаемость; c - скорость света.

Если продифференцировать (1) по

∂

и подставить

∂H

из (3), то полу-

∂t

ε ∂2 E

∂H

εµ ∂2 E

чим

= ×

или

= ××E

. Преобразуем правую

c ∂t

∂t

)

(

−∆Е.

часть по формуле: × ×E

Итак, для векторного поля E имеем уравнение ∂2 Е = c2 ∆E .

∂t2 εµ

Это одно из основных уравнений математической физики, называемое вол-

новым уравнением.

В результате изучения материала, изложенного в этих лекциях, студент должен владеть следующими понятиями и уметь вычислять:

скалярное и векторное поля, способы наглядного описания (поверхности и линии уровня, векторные линии); интегральные характеристики векторного поля:

поток, способы его вычисления, физический смысл; линейный интеграл, способы вычисления, физический смысл;

дифференциальные характеристики скалярного и векторного полей: градиент, его свойства и способы вычисления; дивергенция, ее свойства и способы вычисления; ротор, его свойства и способы вычисления;

связь между дифференциальными и интегральными характеристиками (теорема Остроградского – Гаусса, теорема Стокса); инвариантные определения дифференциальных характеристик; специальные виды векторных полей, их свойства; операторы Гамильтона и Лапласа.

Лекции 10 - 11 ЧИСЛОВЫЕ РЯДЫ

В лекциях 10 – 11 рассматриваются числовые ряды – важнейшее средство изображения, изучения и приближенного вычисления чисел и функций. Приведены основные положения, позволяющие исследовать вопрос о сходимости ряда и, в отдельных случаях, приближенно вычислять значение суммы ряда.

10.1.Числовые ряды. Общие положения

10.2.Ряды с положительными членами

10.3.Теоремы сравнения рядов c положительными числами

11.1.Достаточные признаки сходимости числовых рядов

сположительными членами

11.1.1.Признак Даламбера

11.1.2.Признак Коши

11.1.3.Интегральный признак сходимости

11.2.Знакопеременные ряды

11.3.Знакочередующиеся ряды. Признак Лейбница

10.1.Числовые ряды. Общие положения

∞

О Выражение ∑un = u1 +u2 +…+ un +… где {un} - заданная бесконеч-

n=1

ная числовая последовательность, называется числовым рядом, а

числа un - членами ряда.

ОКонечные суммы S1 = u1 , S2 = u1 +u2 ,..., Sn = u1 +u2 +…+un называются

частичными суммами ряда.

ОЕсли существует конечный предел последовательности частичных

сумм S = lim Sn , то ряд называется сходящимся, а число S - суммой

n→∞

ряда. В противном случае (Sn → ∞, S ) ряд расходится и суммы не имеет.

Пример:

∞

Исследуйте на сходимость ряд:

∑

n=1 n(n +1)

Частичная сумма

Sn =

+…+

n(n +1)

2 2 3

Разложим

на сумму простейших дробей:

−

n(n +1)

n +1

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.2019861.18 Кб53Лекции РИМ сводная_1.doc
#
17.11.2019235.52 Кб5Лекции РЦБ - кусочки.doc
#
21.12.2018681.98 Кб40Лекции сенсоры.doc
#
24.08.2019642.56 Кб28Лекции сенсоры.doc
#
23.02.2015732.41 Кб12лекции сист эл снабж.pdf
#
23.02.20153.38 Mб58Лекции Соболева часть 3.pdf
#
22.02.20151.15 Mб282Лекции соц психология.doc
#
23.02.20154.81 Mб90Лекции Стечкина по матану.pdf
#
21.12.201816.1 Mб40Лекции ТЭПП.doc
#
31.08.2019196.83 Кб7Лекции Философия.docx
#
20.09.20191.05 Mб13лекции ЦБ.docx