
Лекции Соболева часть 3
.pdfФедеральное агентство по образованию ГОУВПО «Уральский государственный технический университет – УПИ»
А.Б. Соболев, А.Ф. Рыбалко
МАТЕМАТИКА
Курс лекций для технических университетов
Часть 3
Екатеринбург
2005
УДК 51/075.8 ББК 22.1я73
С54
Рецензенты:
зав. кафедрой физики УГЛУ, доктор физ-мат. наук, проф. М.П. Кащенко, зав. лабораторией ИФМ УрО РАН, доктор физ-мат. наук, проф. А.П. Танкеев
А.Б. Соболев, А.Ф. Рыбалко
С54 Математика: Курс лекций для технических вузов / А.Б. Соболев, А.Ф. Рыбалко. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. 136 с.
ISBN 5-321-00532-Х
Курс лекций по дисциплине ЕН.Ф.01 «Математика» предназначен для студентов, изучающих данную дисциплину в объеме 540 – 800 часов в течение 4 семестров. Содержание лекций соответствует ГОС и рабочим программам технических специальностей.
Третья часть включает 16 лекций и содержит материал, обычно изучаемый в третьем семестре, – кратные и криволинейные интегралы, элементы теории поля, числовые и функциональные ряды, ряды и интеграл Фурье.
Электронная версия книги, используемая в аудиториях, сопровождается дополнительным иллюстративным материалом.
Наряду с курсом лекций существуют пособия, рассматривающие решение типичных задач и способствующие усвоению понятий и методов.
|
ББК 51 (075.8) |
|
УДК 22.1я 73 |
ISBN 5-321-00532-Х |
© ГОУ ВПО «Уральский государственный |
|
технический университете – УПИ», 2005 |
|
© А.Б. Соболев, А.Ф. Рыбалко, 2005 |

ПРЕДИСЛОВИЕ
Курс лекций предназначен для студентов технических университетов и состоит из четырех частей, в которых излагается теоретический материал курса математики для инженеров.
Втретьей части излагаются следующие разделы: кратные и криволинейные интегралы, элементы теории поля (векторного анализа), числовые и функциональные ряды, ряды и интеграл Фурье.
Вначале каждой лекции приведены заголовки разделов. В совокупности эти заголовки образуют программу дисциплины и являются базой вопросов для тестовых и экзаменационных заданий. Звездочкой помечены разделы, предназначенные для более глубокого изучения. В конце каждой лекции приведен список ключевых понятий.
Влекциях студент найдет основные определения, формулировки теорем, примеры, демонстрирующие методы решения типичных задач. Если отсутствуют доказательства каких–либо утверждений, то формулировки результатов сопровождаются примерами, разъясняющими их смысл.
Втексте приняты следующие условные обозначения:
Оопределение
Ттеорема
Сследствие
!замечание

Лекции 1 - 4 КРАТНЫЕ ИНТЕГРАЛЫ
При изучении физики, механики и при решении разнообразных инженерных задач часто возникает необходимость наряду с интегралами от действительной функции одного переменного рассматривать интегралы от функций многих переменных. Таким образом, приходится вычислять интегралы по двумерным и трехмерным областям, по кривым и поверхностям, что приводит к необходимости знать кратные, криволинейные и поверхностные интегралы.
Изложение этих вопросов проводится в единой схеме, чем обусловлено введение понятия интеграла по фигуре.
1.Интегралы по фигуре
1.1.Основные определения
1.2.Задача об отыскании массы тела
1.3.Определение интеграла по фигуре
1.4.Классификация интегралов по фигуре
1.5.Свойства интегралов по фигуре, определяемые равенствами
1.6.Свойства интегралов по фигуре, определяемые неравенствами (оценка интегралов по фигуре)
2.Двойной интеграл
2.1.Геометрический смысл двойного интеграла
2.2.Вычисление двойного интеграла
2.3.Замена переменных в двойном интеграле
2.4.Двойной интеграл в полярных координатах.
2.4.1. Дифференциальный элемент площади
в полярной системе координат
3.Поверхностный интеграл первого типа (рода)
3.1.Вычисление поверхностных интегралов первого рода
4.Тройной интеграл
4.1.Задача о вычислении массы тела
4.2.Замена переменных в тройном интеграле
4.3.Тройной интеграл в цилиндрических координатах
4.4.Элемент объема в цилиндрических координатах
4.5.Тройной интеграл в сферических координатах
4.6.Элемент объема в сферических координатах
5.Криволинейные интегралы первого типа (рода)
5.1.Способы вычисления криволинейного интеграла первого типа
5.1.1.Криволинейный интеграл первого типа по плоской кривой
5.1.2.Криволинейный интеграл первого типа по пространственной кривой
5.2.Геометрический смысл линейного интеграла по плоской кривой
6.Механические приложения интегралов по фигуре
6.1.Длина, площадь, объем фигуры
6.2.Масса фигуры
6.3.Момент инерции фигуры
6.4.Статические моменты фигуры. Центр тяжести фигуры
2 |
Лекция 1 - 4 |
1. Интегралы по фигуре
1.1. Основные определения
ОПод фигурой (множеством) Ф будем понимать:
1.Отрезок [a,b] оси OX.
2.Плоскую область D плоскости XOY.
3.Часть трехмерного пространства G.
4.Плоскую или пространственную кривуюL , задаваемую уравнениями:
f (x, y)
f (P)= f1 (x, y, z), где P(x, y, z) – точка трехмерного пространства.
2
5. Поверхность ∑ в пространстве.
О
О
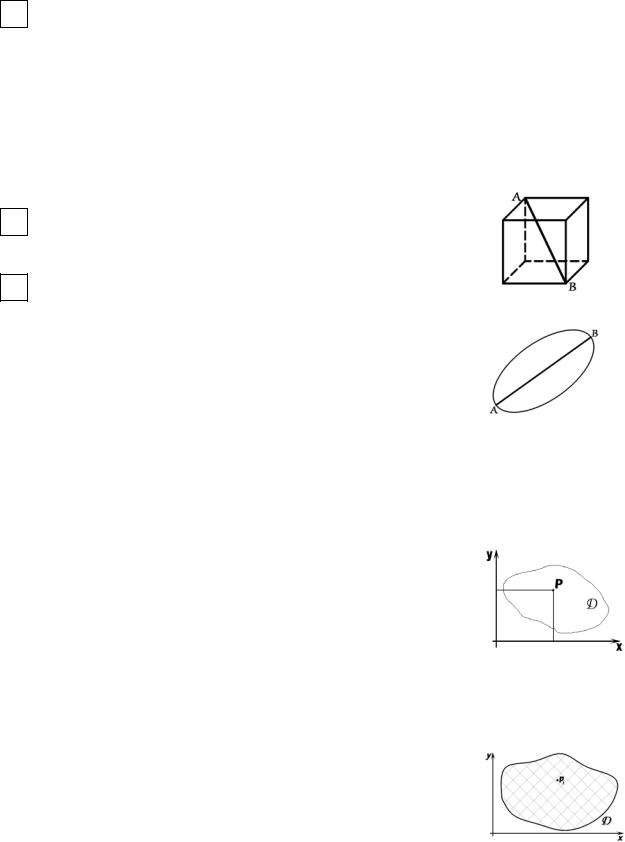
Диаметром d фигуры Ф называется максимальное расстояние между двумя точками фигуры. На рисунке d = AB .
Под мерой µ будем понимать для фигур:
1.Длину отрезка [a,b], µ = b − a .
2.Площадь плоской области D, µ = S .
3.Объем фигуры G, µ =V .
4.Длину кривой L, µ = l .
5.Площадь поверхности ∑ , µ = Sповерх. .
1.2. Задача об отыскании массы тела
Предположим, что фигура Ф обладает массой, которая (масса) распределена с плотностью ρ(P) в
каждой точке P(x, y, z) Φ . Зададим плотность в виде:
ρ(x) - случай {1}
ρ(P)= ρ(x, y) - {2}
ρ(x, y, z) - {3-5}
Найдем массу фигуры в случае 2 (Ф - часть плоско-
сти XOY): ρ(P)= ρ(x, y)
1. Рассмотрим случай однородного распределения плотности по фигуре, т.е. ρ(P)=const. Следователь-
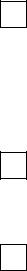
Кратные интегралы |
3 |
но, m = ρ(P) µ . |
|
2. В случае, если ρ(P) ≠ const, разобьем фигуру Ф произвольным образом на n элементарных областей Фi и выберем точку Pi Φi . Пусть n достаточно велико, чтобы полагать в каждой элементарной фигуре ρ(Pi ) ≈const. Обозначим∆µi - меру каждой элементарной фигуры Фi. Масса элементарной фигу-
n
ры: ∆mi ≈ ρ(Pi )∆µi . Масса всей фигуры m ≈ ∑ρ(Pi )∆µi .
i=1
1.3. Определение интеграла по фигуре
Пусть дана фигура Ф и функция f (P), P Φ , определенная на множе-
стве Ф. Разобьем фигуру Ф произвольным образом на n элементарных областей Фi и выберем точку Pi Φi . Найдем диаметр каждой элементарной фигу-
ры Фi и обозначим максимальную из величин di за rn = max{di}. Назовем rn
рангом разбиения. При n → ∞ rn → 0 . Найдем f (Pi ) и составим интеграль-
n
ную сумму вида: Sn = ∑ f (Pi )∆µi .
i=1
ОИнтегралом по фигуре Ф (обозначение ∫ f (P)dµ ) будем называть пре-
Ф
дел интегральной суммы Sn при rn → 0, если этот предел существует и не зависит от способа дробления и выбора точек Pi . Таким образом,
|
|
n |
|
∫ f (P)dµ = limr →0 ∑ f (Pi |
)∆µi , Ф - область интегрирования. |
||
Ф |
n |
i=1 |
|
|
|
||
ТТеорема существования интеграла по фигуре. Если f (P) непрерывна
влюбой точке P замкнутой области Ф, то интеграл по фигуре сущест-
вует.
ООбласть Ф называется замкнутой, если она ограничена замкнутой линией, и точки, лежащие на границе, принадлежат области Ф.
1.4. Классификация интегралов по фигуре
1. Пусть фигура – часть прямой, Φ ↔ [a,b], f (P)= f (x), dµ = dx ,
∫f (P)dµ = ∫b f (x)dx - определенный интеграл на отрезке [a,b].
Φa
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекция 1 - 4 |
2. |
Фигура |
– |
часть |
|
плоскости xOy, |
Φ ↔ D , |
f (P) = f (x, y), |
dµ = dS , |
|||||||
|
∫ f (P)dµ = ∫∫ f (x, y)dS |
– двойной интеграл от функции f (P) = f (x, y) |
|||||||||||||
|
Φ |
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
по области D. |
|
|
|
|
|
|
|
|
Φ ↔ G , |
f (P) = f (x, y, z), |
||||
3. |
Фигура |
– |
пространственная |
область, |
|||||||||||
|
dµ = dV , |
∫ f (P)dµ = ∫∫∫ f (x, y, z)dv |
– тройной интеграл от функции |
||||||||||||
|
|
|
Φ |
|
|
|
G |
|
|
|
|
|
|
|
|
|
f (P) = f (x, y, z) |
по области G. |
|
|
|
|
|
|
|||||||
4. |
Фигура |
– |
линия |
на |
плоскости |
или |
в |
пространстве, |
Φ ↔ L , |
||||||
|
f (P)= |
f |
(x, y) |
|
, |
dµ = dl , |
∫ f |
(P)dµ = ∫ f (x, y, z)dl |
– криволинейный |
||||||
|
|
(x, y, z) |
|||||||||||||
|
|
f |
|
|
|
Φ |
|
L |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интеграл от функции f (P) по кривой L. |
|
|
|
|
||||||||||
5. |
Фигура |
|
– |
поверхность, |
|
Φ ↔ ∑ , f (P) = f (x, y, z), |
dµ = dσ , |
||||||||
|
∫ f (P)dµ = ∫∫ |
f (x, y, z)dσ |
– |
поверхностный |
интеграл от |
функции |
|||||||||
|
Φ |
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
f(P) = f (x, y, z) по области ∑ .
1.5.Свойства интегралов по фигуре, определяемые равенствами
Доказательства свойств следуют из определения интеграла по фигуре. Пусть интеграл по фигуре существует, тогда:
1.∫cf (P)dµ = c∫ f (P)dµ , с = const.
ΦΦ
Доказательство:
∫сf (P)dµ = lim ∑cf (Pi )∆µi
Φrn →0 i=1n
|
n |
|
= c limr →0 ∑ f (Pi |
)∆µi = c∫ f (P)dµ . |
|
n |
i=1 |
Φ |
|
||
2. ∫( f (P)± g (P))dµ = ∫ f (P)dµ ± ∫g (P)dµ .
Φ Φ Φ
3.Свойство аддитивности. Пусть фигура Ф состоит из двух частей, т.е.
Φ =Φ1 Φ2 , тогда ∫ f (P)dµ = ∫ f (P)dµ + ∫ f (P)dµ .
Φ |
Φ1 |
Φ2 |

Кратные интегралы |
5 |
1.6.Свойства интегралов по фигуре, определяемые неравенствами (оценка интегралов по фигуре)
1. |
Если для любой точки P Ф |
f (P)≥ 0 , то ∫ f (P)dµ ≥ 0 . |
|
|
|
Φ |
|
2. |
Если для любой точки P Ф |
f (P)≥ g (P), то ∫ f (P)dµ ≥ ∫g (P)dµ . |
|
|
|
Φ |
Φ |
3.Если существуют такие два числа m, M, что m ≤ f (P)≤ M , то
mµ ≤ ∫ f (P)dµ ≤ M µ, где µ −мера Ф.
Φ
Пример:
1) m(b −a)≤ ∫b f (x)dx ≤ M (b −a).
a
2) mS ≤ ∫∫ f (x, y)dS ≤ MS .
D
3) mV ≤ ∫∫∫ f (x, y, z)dv ≤ MV .
G
4) mL ≤ ∫ f (x, y, z)dl ≤ ML .
L
5)mSпов ≤ ∑∫∫ f (x, y, z)dσ ≤ MSпов .
ТТеорема о среднем. Если функция f (P) непрерывна в замкнутой
ограниченной области Ф, то существует точка P Φ , такая, что выполняется равенство: ∫ f (P)dµ = µ f (P).
Φ
Физический смысл теоремы о среднем
Пусть фигура Ф обладает массой, распределенной с плотностью f (P)= ρ(P), тогда m = ∫ f (P)dµ = µ f (P). В случае пространственной фи-
Φ
гуры мера фигуры равна объему µ =V , m =V ρ(P), ρ(P)= Vm - среднее зна-
чение плотности.
6 |
Лекция 1 - 4 |
Геометрический смысл интегралов по фигуре
Пусть f (P) ≡1, тогда интеграл по фигуре будет равен мере соответствующей фигуры, т. е. ∫dµ = µ . В частных случаях:
|
|
|
|
Φ |
1. |
∫b dx = b − a - длина отрезка [a,b]. |
|||
|
a |
|
|
|
2. |
∫∫dS = S - площадь области D. |
|||
|
D |
|
|
|
3. |
∫∫∫dV =V - объем пространственной области G. |
|||
|
G |
|
|
|
4. |
∫dl = L - длина линии L. |
|||
|
L |
|
|
|
5. |
∑∫∫ |
dσ = S |
∑ |
- площадь поверхности ∑ . |
|
|
|||
Механический смысл интегралов по фигуре
Если функция f (P) = ρ(P) является плотностью фигуры, то масса фигуры выражается интегралом по фигуре
∫ρ(P)dµ = m .
Ф
2. Двойной интеграл
Рассмотрим фигуру, которая является частью плоскости xOy: Φ ↔ D . Интеграл по фигуре в данном случае является двойным интегралом от функ-
n
ции f(P)= f (x, y) по области D: ∫∫ f (P)dS = lim Σ f (Pi )∆Si .
D
rn →0 i=1
Кратные интегралы |
7 |
2.1. Геометрический смысл двойного интеграла
Задача о вычислении объема тела
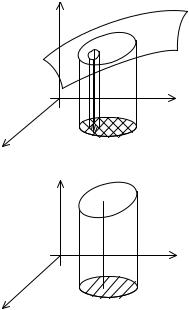
Найдем объем тела, ограниченного сверху непрерывной поверхностью z = f (x, y) , снизу
замкнутой областью D плоскости xOy и сбоку
цилиндрической поверхностью, образующие которой параллельны оси Oz, а направляющей является граница Г области D .
Разобьем основание D на конечное число элементарных ячеек ∆S1,∆S2 ,...,∆Sn . В каждой
ячейке выберем точку Mi (xi , yi ) ∆Si (i =1,2,...n) и построим столбик с основанием ∆Si и высотой
Mi Ni = f (xi , yi ) .
Если приближенно принять каждый столбик за прямой цилиндр, то в этом приближении его объем равен ∆Vi ≈ f (xi , yi ) ∆Si , а объем всего те-
z
0
x
z
0
x
n
ла приближенно равен V ≈ ∑ f (xi , yi )∆Si . Перейдем к пределу
|
i=1 |
|
|
|
|
|
n |
∫∫ |
|
∫∫ |
|
rn →0 i=1 |
|
|
|||
V = lim |
∑ f (xi , yi )∆Si = |
|
f (x, y)dS = |
|
f (P)dS . |
|
|
D |
|
D |
|
z = f (x, y)
y
D
Γ
 Ni
Ni
y
 Mi ∆Si
Mi ∆Si
Вывод: если f (x, y) ≥ 0 , то ∫∫ f (x, y)dS представляет объем криволинейного
D
цилиндра, построенного на области D и ограниченного сверху поверхностью f (x, y) .
2.2. Вычисление двойного интеграла
Рассмотрим |
прямоугольную |
область интегрирования D ={x [a,b]; |
y [c, d ]}. Найдем объем тела, ограниченного поверхностью z = f (x, y) , |
||
плоскостью z = 0 |
и цилиндрической поверхностью, образующие которой па- |
|
раллельны оси Oz, а направляющей служит граница области D . |
||
Вычислим объем по площадям параллельных сечений. |
||
Проведем плоскость x = const |
(a < x < b) . Фигура, получающаяся в се- |
|
чении, представляет собой |
криволинейную трапецию, ограниченную линия- |
ми: z = f (x, y) (x = const) , |
z = 0 , y = c , y = d . Площадь сечения равна: |
S(x) = ∫d f (x, y)dy .
c
Объем всего тела равен
