Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции Соболева часть 3

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

3.38 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1414

128						Лекции 15 - 16
e	iϕ	= cosϕ + isinϕ , cosϕ =	eiϕ +e−iϕ	, sinϕ =	eiϕ −e−iϕ	.
e		= cosϕ + isinϕ , cosϕ =	2	, sinϕ =	2i	.
			2		2i

Обозначим πl = ω.

Тогда

∞

einωx + e−inωx

einωx − e−inωx

f (x)

+ ∑ an

+bn

n=1

∞ a

−ib

+ib

∞

−ib

+ib

+ ∑

einωx +

e−inωx =

+ ∑

einωx +

e−inωx

n=1

∞

или

f (x)= c0 + ∑(cneinωx +c−ne−inωx ), где введены обозначения:

n=1

c0 =

, cn =

an −ibn

, c−n

an + ibn

, n N .

Получим выражения для комплексных коэффициентов cn

и c−n :

−ib

1 l

cn =

∫ f (x) cos nωx dx −i

∫ f (x)sin nωx dx

−l

l −l

∫ f (x)[cos(−nωx) +i sin(−nωx)]dt

∫ f (x)e−inωx dx.

−l

+ib

Аналогично для c

имеем c

f (x)einωx dx , где n =1,2,...

−n

2l −∫l

При n = 0 имеем c

f (x)dx .

2l −∫l

Если считать номер n не натуральным, а целым числом, n = 0,

±1,

±2, ... ,

все формулы для вычисления коэффициентов ряда можно записать единооб-

разно: c =	1	l	f (x)e−inπl	x dx , n = 0, ±1, ±2, ... , а сам ряд Фурье в виде
разно: c =		l	f (x)e−inπl	x dx , n = 0, ±1, ±2, ... , а сам ряд Фурье в виде
n	2l −∫l
	2l −∫l
				∞	inπx
				f (x)= ∑cne l .

n=−∞

Ряды Фурье

129

Эта сумма называется рядом Фурье в комплексной форме, слагающие ее

функции

c e

inπ x

комплексными

гармониками,

коэффициенты

cn - комплексными амплитудами гармоник.

c0 =

−∫π

f (x)dx = 0 ;

2π

−inx

cn =

∫ f

(x)e

dx =

∫

f (x)e

dx + ∫ f (x)e

2π

−π

−inx

−π

−inx

e−inπ

+einπ

−2

− ∫ e

dx +

∫e

dx =

∫ +

∫

2π

−2πni

2π −π

1−cosπn

n = 2m,

m Z.

πni

iπ

(2m +1), n = 2m +1,

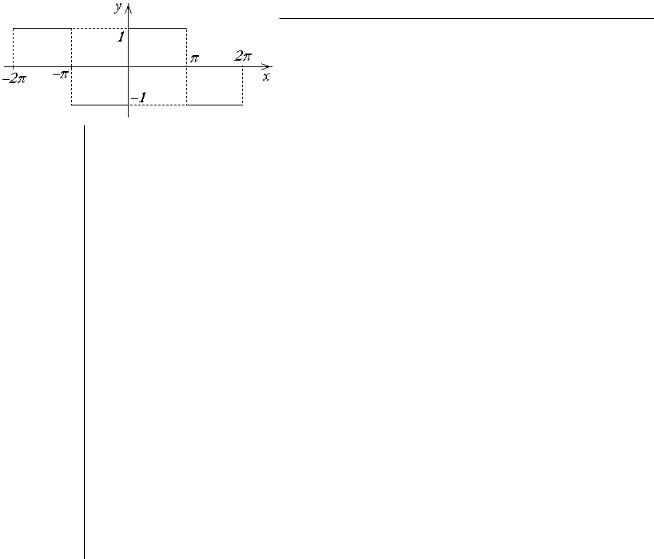
Пример:

Разложить в комплексный ряд Фурье периодическую функцию

f (x) с периодом 2π, если на

[−π;π].

1, x [0,π];

f (x)= ( )

−1, x −π, 0 .

Решение:

Вычислим комплексные коэффициенты Фурье:

f (x)dx = 0 ;

2π −∫π

−inx

cn =

∫

f (x)e

dx =

∫

f (x)e

dx +

∫ f (x)e

2π

−π

−inx

−π

−inx

e−inπ +einπ −2

− ∫ e

dx + ∫e

∫

+ ∫

dx =

2π

−2πni

2π −π

1−cosπn

0, n = 2m,

m Z.

πni

iπ (2m +1), n = 2m +

130

Лекции 15 - 16

Выпишем разложение f (x):

∞

i(2m+1)x

f (x)

∑

iπ m=−∞ (2m +1)

−ix

e3ix

−e−3ix

e5ix −e−5ix

−e

...

iπ

−e

−ix

3ix

−e

−3ix

5ix

−e

−5ix

+...

3 2i

5 2i

sin x

sin 3x

sin 5x

∞

sin

(

2n +1 x

∑

)

+...

2n +1

π n=0

Как видно, по комплексной форме ряда Фурье легко восстанавливается его обычный вид (обычное разложение было получено ранее, стр. 74).

16.5. Интеграл Фурье

Функцию f (x), удовлетворяющую на отрезке [−l;l] условиям теоремы Дирихле, можно разложить в ряд Фурье:

f (x)= a0 + ∑∞ (an cos kn x +bn sin kn x); 2 n=1

где	an =	1 l	f (x)cos kn x dx , (n = 0,1, 2,...);
		l −∫l
	b	= 1 l		f (x)sin k			n	x dx , (n =1,2,...),
	n	l −∫l					n
		l −∫l
и введено обозначение: kn				=	πn	(так называемые волновые числа).
и введено обозначение: kn				=		(так называемые волновые числа).
					l
Функция	f (x) может быть периодической с периодом 2l или непе-

риодической. В последнем случае предполагается, что с отрезка [−l;l]

на всю числовую ось функция продолжена периодически.

Рассмотрим случай, когда непериодическая функция задана на всей числовой оси (−∞;∞), на любом конечном отрезке [−l;l] удовлетворяет усло-

Ряды Фурье

131

виям теоремы Дирихле и абсолютно интегрируема на всей числовой

∞

(x)

оси, т.е. ∫

dx = M < ∞ .

−∞

Подставим в ряд значения коэффициентов an

и bn :

∞

f (x)=

−∫l

f (t)dt + ∑n=1

1l −∫l

f (t)(cos kn x cos knt +sin kn x sin knt)dt =

∞ l

∫ f (t)cos knt dt +1

∑∫ f (t) cos kn (x −t)dt .

−l

n=1 −l

Устремим l

к бесконечности. Предел первого слагаемого

f (t)dt

≤ lim

f (t)

dt ≤ lim

1 ∞

f (t)

dt = lim

= 0 .

lim

2l −∫l

2l −∞∫

l→∞

Преобразуем второе слагаемое (сумму):

∞ l

∞

∑∫ f (t) cos kn

(x −t)dt =

∑F (kn ), где F (kn )= ∫ f (t) cos kn (x −t)dt

n=1 −l

n=1

−l

(этот интеграл зависит и от x , но в данном случае нас интересует только зависимость от волновых чисел kn ).

Заметим, что волновые числа kn = πln образуют арифметическую про-

грессию с разностью ∆k

π , причем ∆k

→0 . Это позволяет пре-

l→∞

образовать сумму:

1 ∑F (kn )π

= 1

∑F

(kn ) ∆kn ;

1 ∑F (kn )=

∞

n=1

π n=1

последнее представление позволяет рассматривать ряд как интегральную сумму:

	1	∞	1	∞
nlim→∞	1	∑F (kn ) ∆kn =	1	∫F (k )dk ,
nlim→∞	π	∑F (kn ) ∆kn =	π	∫F (k )dk ,
		n=1		0

или

132							Лекции 15 - 16
		1	∞		1	∞	∞
f (x)=			∫F (k )dk =			∫dk ∫ f (t)cos k (x −t)dt .
	π			π
			0			0	−∞

Эта формула называется формулой Фурье, а интеграл, стоящий в правой части, – интегралом Фурье. Функция F (k ) называется

спектральной плотностью.

Это название связано со следующими обстоятельствами: для периодической функции f (x) с периодом 2l набор величин

D =	a	2 +b 2	показывает,	в какой мере в разложении функции f (x)
n	n	n			cos nπ x ,		nπ x
представлены			различные	гармоники		sin		и называется
							l
спектром функции f (x).					l

Для периодической функции f (x)					спектр - функция целочисленно-

го аргумента, т.е. последовательность, величины отдельных членов которой показывает вклад соответствующих гармоник ( f (x) составляется

как сумма бесконечного, но счетного количества гармоник). Для непериодической функции f (x) в разложении ее на простейшие периодиче-

ские составляющие присутствует несчетное количество слагаемых (интеграл), величина F (k )∆k описывает вклад гармоник с волновыми чис-

лами из интервала (k − ∆2k ;k + ∆2k ).

Интеграл Фурье можно представить в виде, подобном ряду Фурье:

f (x)			∞	(A(k )cos kx + B (k )sin kx)dk ,
			= ∫
где			0
		∞					∞
A(k)=	1		f (t)coskt dt,		B(k)=	1
		∫					∫ f (t)sin kt dt ,
	π					π
		−∞					−∞

и введенные ранее амплитуды D (k )= A2 (k )+ B2 (k ).

В результате изучения материала, изложенного в этих лекциях, студент должен знать:

определение тригонометрического ряда и ряда Фурье данной периодической функции; достаточные условия разложимости функции в ряд Фурье (условия Дирихле);

особенности разложений четных и нечетных функций; разложение в ряд Фурье функций произвольного периода;

Ряды Фурье

133

представление непериодической функции рядом Фурье.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1414

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.2019861.18 Кб52Лекции РИМ сводная_1.doc
#
17.11.2019235.52 Кб5Лекции РЦБ - кусочки.doc
#
21.12.2018681.98 Кб40Лекции сенсоры.doc
#
24.08.2019642.56 Кб28Лекции сенсоры.doc
#
23.02.2015732.41 Кб11лекции сист эл снабж.pdf
#
23.02.20153.38 Mб58Лекции Соболева часть 3.pdf
#
22.02.20151.15 Mб282Лекции соц психология.doc
#
23.02.20154.81 Mб90Лекции Стечкина по матану.pdf
#
21.12.201816.1 Mб40Лекции ТЭПП.doc
#
31.08.2019196.83 Кб7Лекции Философия.docx
#
20.09.20191.05 Mб13лекции ЦБ.docx