
Лекции Соболева часть 3
.pdf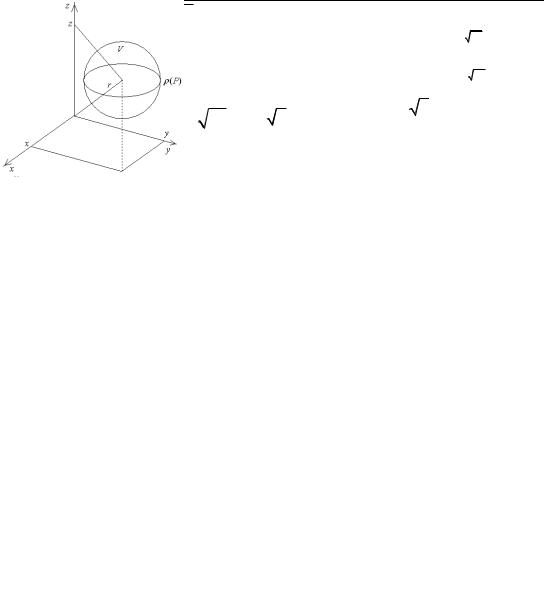
|
28 |
|
|
|
|
|
|
|
|
|
Лекция 1 - 4 |
|
|
|
x = ± 2 y , − 2 y ≤ x ≤ 2 y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2(1− y ) |
|
|
|
|
|
1 |
|
2 y |
|
|
m = ∫∫∫ydxdydz = ∫∫ ydxdy |
∫ dz = ∫∫ y(1− y)dxdy = ∫(y − y2 )dy |
∫ dx = |
||||||||
|
|
V |
D |
1− y |
D |
|
|
|
|
0 |
− |
2 y |
|
|
= ∫1 |
(y − y2 )2 |
|
2 2 y |
|
|
2 y |
|
1 |
|
|
|
|
2 ydy = 2 |
52 |
− |
72 |
= |
8 2 |
|
||||
|
|
0 |
|
|
5 |
|
|
7 |
|
0 |
35 |
|
6.3 Момент инерции фигуры
Рассмотрим систему из n материальных точек с массами mi , i =1,2,...,n . Момент инерции системы от-
n
носительно некоторой оси вращения J = ∑ri 2mi , где ri
i=1
— расстояние от i –й точки до оси вращения. Если тело сплошное, то возникает интеграл по фигуре J
= ∫r2 ρ(P)d µ .
Φ
Осевые моменты (моменты инерции фигуры относительно осей координат). Рассмотрим пространственную фигуру Ф→V.
Jx - момент инерции относительно оси Оx (мера
инертности тела при вращении относительно оси Оx):
Jx = ∫∫∫( y2 + z2 )ρ(x, y, z)dV ,
V
J y = ∫∫∫(x2 + z2 )ρ(x, y, z)dV ,
V
Jz = ∫∫∫(x2 + y2 )ρ(x, y, z)dV .
V
Моменты инерции относительно координатных плоскостей:
Jxy = ∫∫∫z2 ρ(x, y, z)dV ,
G
Jxz = ∫∫∫y2 ρ(x, y, z)dV ,
G
J yz = ∫∫∫x2 ρ(x, y, z)dV ,
G
Полярный момент (момент инерции относительно начала координат, где центр О – полюс):
Jo = ∫∫∫(x2 + y2 + z2 )ρ(x, y, z)dV
G

Кратные интегралы |
29 |
Пример:
Найдите момент инерции однородной боковой поверхности цилиндра, задаваемой уравнениями:
|
2 |
+ z |
2 |
= R |
2 |
|
ρ(P) ≡1 |
||
x |
|
|
|
|
|||||
|
π |
≤ y ≤ |
π |
; z ≥ 0 |
J xy = ? |
||||
− |
2 |
2 |
|||||||
|
|
|
|
|
|
||||
Решение:
Jxy = ∫∫z2dσ = ∫∫z2 ( z′x )2 +( z′y )2 +1dS =
∑D
= ∫∫(R |
2 |
− x |
2 |
) 1 + |
|
|
|
x2 |
|
2 dS =∫∫(R |
2 |
− x |
2 |
) R |
|
|
1 |
|
2 dS = |
|||||||||||||
|
|
R |
2 |
− x |
|
|
R |
2 |
− x |
|||||||||||||||||||||||
D |
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
= R∫∫ R2 |
− x2 dxdy = R ∫R |
|
R2 |
− x2 dx ∫2 dy =πR ∫R |
|
|
R2 |
− x2 dx = |
||||||||||||||||||||||||
D |
|
|
|
|
|
|
|
|
|
−R |
|
|
|
|
|
|
|
|
|
− |
π |
|
|
−R |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = R sint |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = Rcostdt |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
sint = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t = arcsin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
≤ t ≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
− |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
=πR ∫2 |
R2 −R2 sin2 tRcostdt =πR ∫2 |
RcostRcostdt = |
|
||||||||||||||||||||||||||||
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= π R |
3 |
2 |
cos |
2 |
tdt = |
|
|
2 |
t |
= |
1 + cos 2t |
|
π 2 R3 |
|
||||||||||||||||||
|
∫ |
|
cos |
|
|
|
|
|
2 |
|
= |
|
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 Лекция 1 - 4
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
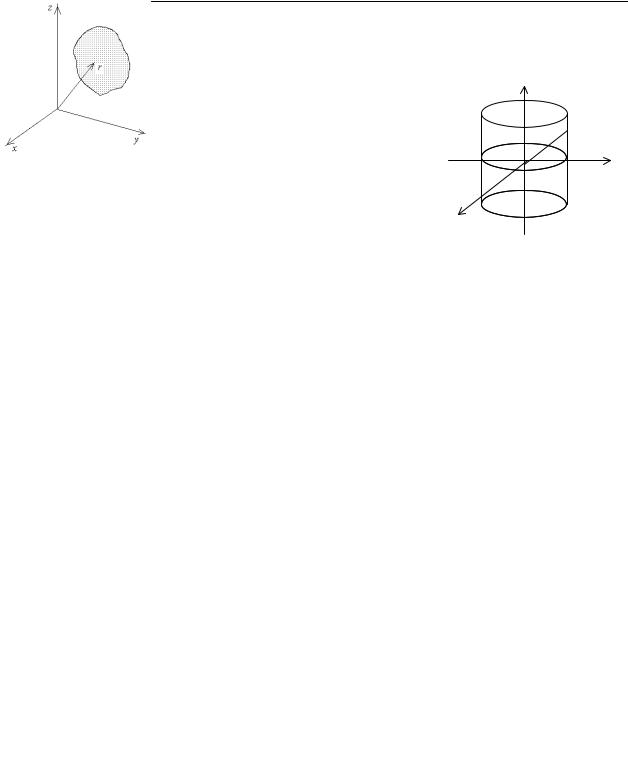
Вычислите момент инерции прямого кругового цилиндра высотой 2h и |
|||||||||||||||||||||||||||||||||||||||||
|
радиусом R относительно диаметра его сред- |
|
|
|
|
|
z |
|||||||||||||||||||||||||||||||||||
|
него сечения, считая плотность постоянной и |
|
|
|
|
|
|
|
h |
|||||||||||||||||||||||||||||||||
|
равной γ0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
I = I x = ∫∫∫(y 2 + z 2 )γ0 dxdydz . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
y |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−h |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Перейдем к цилиндрическим координатам: |
|
|
x |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
x = ρ cosϕ, y = ρ sinϕ, z = z; dxdydz = ρdρdϕdz , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
y 2 + z 2 |
= ρ2 sin2 ϕ + z 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
R |
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|||
|
I = ∫∫∫(ρ2 sin2 ϕ + z 2 )γ0 ρdρdϕdz = 2γ0 ∫dϕ∫ρdρ∫(ρ2 sin2 ϕ + z 2 )dz = |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
R |
|
|
|
|
|
|
|
|
|
z |
3 h |
|
|
|
|
2π |
R |
|
|
|
|
|
|
|
h |
3 |
|
||||||||||
|
= 2γ0 ∫dϕ∫ρdρ ρ |
2 sin2 ϕz + |
|
|
|
|
= 2γ0 ∫dϕ∫ |
ρ ρ |
2 sin2 ϕ h + |
|
dρ = |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
3 |
|
0 |
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
3 |
|
|||||||||||
|
|
|
2π |
|
|
|
2 |
|
ρ4 |
|
h3 ρ2 R |
|
|
|
|
2π |
|
hR4 |
|
|
2 |
|
|
h3 R2 |
|
|
|
|
|
|||||||||||||
|
= 2γ0 ∫dϕ hsin |
|
ϕ |
|
|
+ |
|
|
|
|
|
|
= 2γ0 ∫ |
|
4 |
sin |
|
ϕ + |
6 |
dϕ = |
||||||||||||||||||||||
|
|
4 |
3 |
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2π |
|
|
|
|
1 |
2π |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
2π |
|
1 |
|
|
|
|
|
|
|
|||||||
|
|
∫ |
sin2 ϕ dϕ = |
|
∫ |
(1 − cos 2ϕ)dϕ = |
|
− |
sin 2ϕ |
|
|
= |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
2π = π |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hR |
4 |
h3R2 |
|
= 2γ0hR2π |
R |
2 |
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
= 2γ0 |
|
π + |
|
|
|
|
2π |
|
|
|
|
+ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
4 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6.4. Статические моменты фигуры. Центр тяжести фигуры
Рассмотрим n материальных точек массой mi. Координаты центра тяжести системы точек:
|
|
|
n |
|
|
n |
|
|
|
|
n |
|
X |
|
= |
∑ximi |
;Y |
= |
∑yimi |
; Z |
|
= |
∑zimi |
, |
|
C |
i=1 |
i=1 |
C |
i=1 |
||||||||
n |
|
n |
||||||||||
|
|
C |
|
|
n |
|
|
|
||||
|
|
|
∑mi |
|
|
∑mi |
|
|
|
∑mi |
|
|
|
|
|
i=1 |
|
|
i=1 |
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
M yz |
= ∑ximi |
|
|||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
M xz |
n |
|
|
|
|
||
где величины, равные |
= ∑yimi , называют ста- |
|||||||||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
M xy |
n |
|
|
|
|
||
|
|
|
|
|
= ∑zimi |
|
||||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
тическими моментами системы относительно плоскостей yОz, xОz, xОy.

Кратные интегралы |
31 |
!1). Если система (фигура) имеет центр симметрии, ось симметрии, плоскость симметрии, то статические моменты соответственно относительно центра, оси, плоскости равны нулю.
2). Если фигура непрерывна, то вместо сумм возникают соответствующие интегралы по фигуре
x |
= |
∫xρ(P)dµ |
; y |
= |
∫yρ(P)dµ |
; z |
= |
∫zρ(P)dµ |
. |
|
Φ |
Φ |
Φ |
||||||||
∫ρ(P)dµ |
∫ρ(P)dµ |
∫ρ(P)dµ |
||||||||
C |
|
C |
|
C |
|
|
||||
|
|
Φ |
|
|
Φ |
|
|
Φ |
|
Пример:
Найдите центр тяжести однородного ( γ(P) =1 ) цилин-
z = x2 + y2 +1,
дра, ограниченного поверхностями: x2 + y2 =1, .
z = 0.
Сверху цилиндр ограничен эллиптическим параболоидом.
Решение:
Из соображений симметрии хс= 0, ус= 0, т.к. статические моменты относительно плоскостей ZOY и ZOX равны нулю,
|
z |
= |
|
∫∫∫zγ(P)dV |
|
|
|
|
|||
|
|
V |
|
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
C |
|
|
∫∫∫γ (P)dV |
|
|
|
|
|||
Числитель: |
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 +y2 +1 |
|
|
|
z2 |
x2 |
+y2 +1 |
∫∫∫zγ (P)dV = ∫∫∫zdV |
= ∫∫dS |
∫ |
zdz |
= ∫∫ds |
|
= |
|||||
2 |
|
||||||||||
V |
V |
|
D |
0 |
|
|
D |
|
0 |
||
|
|
|
|
|
|||||||
=1 ∫∫ds(x2 + y2 +1)2 ={в полярных координатах} 2 D
|
|
|
= |
1 |
|
2∫π dϕ∫1 |
(r 2 +1)2 rdr = |
1 |
|
2∫π dϕ∫1 |
(r 2 |
+1)2 d (r 2 |
+1) = |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
2 0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
2 2 0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
= |
1 |
2∫π dϕ |
(r2 +1)3 |
|
|
1 |
= |
1 |
2∫π dϕ |
( |
8 |
− |
|
1 |
) = |
2 |
π |
7 |
= |
7 |
|
π . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
4 |
|
0 |
|
|
|
3 |
|
|
|
|
|
4 |
|
0 |
|
3 |
|
|
|
3 |
|
|
4 |
3 |
6 |
|
|
|
|
|
|
||||||||
Знаменатель: |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x2 +y2 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2π |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∫∫∫dV = ∫∫ds |
|
|
|
∫ |
dz =∫ dϕ∫(r2 +1)rdr = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
V |
|
|
D |
|
|
|
0 |
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
2∫πdϕ |
∫1 (r 2 |
|
|
|
|
|
|
|
|
1 |
2∫πdϕ |
(r 2 +1)2 |
|
1 |
|
1 |
2∫πdϕ(4 −1) = = |
3 |
|
3 |
|
||||||||||||||||||||
= |
+1)d (r 2 +1) = |
|
|
|
= |
2π = |
π . |
||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|||||||||||||||||||||||||||||
|
0 |
0 |
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
2 |
|
|
|
|
|
0 |
4 |
|
0 |
|
|
|
|
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
z |
= 7 π 2 = |
7 |
= 7 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
C |
6 3 |
π |
|
3 3 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

32 |
Лекция 1 - 4 |
Ответ: xc=0, yc=0, zc= 79 .
Пример:
Определите координаты центра тяжести верхней половины шара радиусом R с центром в (0,0,0) , считая плотность γ0 постоянной.
Решение:
z = R2 − x2 − y2 ; z = 0; 0 ≤ z ≤ R2 − x2 − y2 .
x |
= y |
= 0, |
z |
|
= |
∫∫∫zγ0dxdydz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
V |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
∫∫∫γ0dxdydz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
c |
|
c |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В сферических координатах: |
|
z = ρ cosθ, dxdydz = ρ2 dρ sinθdθdϕ . |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
π 2 |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
m = ∫∫∫γ0 ρ2d ρ sinθdθdϕ = ∫ dϕ ∫ |
dθ∫γ0 ρ2d ρ sinθ = |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
π 2 |
|
|
|
|
|
ρ3 |
|
R |
|
R3 |
π 2 |
|
|
|
2πγ0 R |
3 |
|
(−cosθ ) |
|
π0 |
2 = |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
= 2πγ0 |
∫ dθ sinθ |
|
|
|
= 2πγ0 |
∫ sinθdθ = |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
3 |
|
|
|
3 |
|
3 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
2πγ R3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
π 2 |
|
|
|
|
|
|
|
|
|
R |
|
|||
∫∫∫γ0 ρ cosθρ2 s inθd ρdθdϕ =γ0 ∫ dϕ ∫ |
cosθ sinθdθ ∫ρ3d ρ = |
|
|||||||||||||||||||||||||||||||||||||
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
0 |
|
|
|
||||
|
|
|
|
R4 π 2 |
|
|
|
|
|
|
|
|
|
|
|
πγ |
0 |
R4 sin2 θ |
|
π 2 |
πγ |
0 |
R4 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
=γ0 2π |
|
|
|
∫ sinθd (sinθ) = |
|
|
|
|
|
|
|
= |
|
|
|
|
. |
|
|
|
|||||||||||||||||||
4 |
|
|
|
2 |
|
|
2 |
|
|
4 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||
z |
|
= |
πγ0 R4 |
|
3 |
|
|
|
= |
|
3 |
R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2πγ |
|
R3 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
c |
|
|
4 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: xc=0, yc=0, zc= 83 R .
В результате изучения материала, изложенного в этих лекциях, студент должен знать следующие понятия и уметь вычислять:
интегралы по фигуре, их классификацию и свойства; двойной интеграл, вычисление двойного интеграла как повторного;
замена переменных в двойном интеграле, двойной интеграл в полярных координатах; поверхностный интеграл первого рода, способы вычисления;
тройной интеграл, вычисление тройного интеграла как повторного; способы его вычисления, замена переменных в тройном интеграле; тройной интеграл в цилиндрических координатах; тройной интеграл в сферических координатах;
криволинейный интеграл первого рода, способы вычисления; геометрические и механические приложения интегралов по фигуре: длина, площадь, объем, масса фигуры; центр тяжести, статические моменты, моменты инерции фигуры.

Лекции 5 – 9 ТЕОРИЯ ПОЛЯ (ВЕКТОРНЫЙ АНАЛИЗ)
Теория поля (или векторный анализ) изучает скалярные и векторные поля, т.е. скалярные и векторные функции точки в пространстве. Хотя объекты теории не связаны с ка- кой-либо системой координат, использование этого инструмента позволяет, исследуя средствами математического анализа функции нескольких переменных (которыми становятся функции точки), определить координатно независимые операции над полями и изучить их свойства. В этом векторный анализ, как раздел векторного исчисления, полностью аналогичен векторной алгебре – хотя операция над векторами может быть сведена к вычислениям, проводимым над координатами векторов, результат от координатной системы не зависит.
Понятие поля позволяет наиболее естественно характеризовать и описывать те свойства реальных объектов, которые не зависят от выбора системы координат: реальные физические свойства не должны быть связаны с какой-либо системой координат.
5.Общие понятия
5.1.Скалярное поле
5.2.Поверхности и линии уровня
5.3.Производная по направлению
5.4.Градиент скалярного поля
5.4.1.Оператор Гамильтона (набла)
5.4.2.Связь производной по направлению с градиентом
5.4.3.Свойства градиента
5.5.Векторное поле
5.5.1.Векторные линии
5.5.2.Плоское векторное поле
6.Поверхностные интегралы
6.1.Односторонние и двусторонние поверхности
6.2.Площадь поверхности
6.3.Система координат и ориентация поверхности
6.4.Поверхностный интеграл 1-го рода
6.5.Поверхностный интеграл 2-го рода
7.Поток векторного поля
7.1.Определение потока векторного поля
7.2.Свойства потока
7.3.Вычисление потока
7.3.1.Проектирование на одну координатную плоскость
7.3.2.Проектирование на три координатные плоскости
7.4.Физический смысл потока
7.5.Дивергенция векторного поля
7.5.1.Свойства дивергенции
7.6.Физический смысл потока через замкнутую поверхность
7.7.Теорема Остроградского – Гаусса
7.8.Инвариантное определение дивергенции
7.8.1.Физический смысл дивергенции
8.Линейный интеграл в векторном поле
34 |
Лекция 5 - 9 |
8.1.Понятие линейного интеграла
8.2.Свойства линейного интеграла
8.3.Вычисление линейного интеграла
8.4.Физический смысл линейного интеграла
8.5.Ротор (вихрь) векторного поля
8.5.1.Свойства ротора (вихря)
8.6.Теорема Стокса
8.7.Инвариантное определение ротора
8.8.Физический смысл ротора
8.9.Формула Грина
9.Специальные виды векторных полей
9.1Потенциальное векторное поле
9.1.1.Условия потенциальности поля
9.1.2.Вычисление потенциала поля
9.2Соленоидальное поле
9.2.1.Свойства соленоидального поля
9.3.Операторы Гамильтона и Лапласа
9.3.1.Оператор Гамильтона (набла)
9.3.2.Оператор Лапласа
5. Общие понятия
5.1. Скалярное поле
ОЕсли с каждой точкой P(x, y, z) некоторой пространственной области G
связана скалярная величина, то говорят, что в области G задано скалярное поле: u = f (x, y, z) , где f (x, y, z) - скалярная функция, назы-
ваемая функцией поля.
Примеры скалярных полей: поле температур, поле давления, поле плотности, поле концентраций, поле электрического потенциала. Рассмотрим подробнее последний пример.
Пусть речь идет о точечном заряде q. Потенциал электростатического поля заряда q, помещенного в начало координат, задается в каждой точке
пространства r(x, y, z) , за исключением начала координат, функцией поля вида:
u = q |
= |
|
q |
= |
q |
. |
|
r |
x2 + y2 + z2 |
||||
r |
|
|
|
|
Теория поля |
35 |
Заметим, что если r = const , x2 + y2 + z2 = const - уравнение сферы. Следова-
тельно, в точках, принадлежащих сфере, потенциал электростатического поля сохраняет свое значение, или u = const .
Ограничимся рассмотрением так называемых стационарных полей, т.е. полей, не зависящих от времени.
5.2. Поверхности и линии уровня
В дальнейшем, если не оговорено особо, предполагаем функцию u = f (x, y, z) однозначной и непрерывно-дифференцируемой.
Рассмотрим точки области, в которой функция u = f (x, y, z) принимает постоянные значения: f (x, y, z) = c, (c = const) . Это уравнение можно рассматривать как уравнение некоторой поверхности в пространстве.
ОГеометрические места точекP(x, y, z) , где скалярное поле принимает одно и то же значение f (x, y, z) = c , называются поверхностями уровня
или эквипотенциальными поверхностями.
!В силу однозначности функции u = f (x, y, z) поверхности уровня, соот-
ветствующие различным значениям c, не пересекаются между собой.
ОСкалярное поле называется плоским, если при подходящем выборе системы координат функция поля зависит только от двух переменных. Множество точек плоскости P(x, y) , для которых f (x, y) = c , называется линией уровня плоского скалярного поля.
Пример:
Поле температур бесконечной равномерно нагретой нити.
линии уровня – окружности
5.3. Производная по направлению
Пусть в пространственной области G задано скалярное поле:
u = u(x, y, z) = u(P) . |
Рассмотрим точку P1(x, y, z) и исходящий из нее вектор |
|||||||||
l ={lx ;ly ;lz }. |
Найдем, |
как изменяется поле в направлении вектора l . Сме- |
||||||||
стимся |
из |
точки |
P1(x, y, z) в |
направлении вектора l |
|
в |
|
|
точку |
|
P (x + ∆x, y + ∆y, z + ∆z) . Обозначим за |
∆l длину вектора PP : ∆l = |
|
PP |
|
, тогда |
|||||
|
|
|||||||||
2 |
|
|
|
1 |
2 |
|
1 |
2 |
|
|
∆l = |
∆x2 + ∆y2 + ∆z2 . При этом функция поля получит приращение |
|
|
|
||||||

36 |
Лекция 5 - 9 |
∆u = u(P2 ) −u(P1 ) = u(x + ∆x, y + ∆y, z + ∆z) −u(x, y, z)
= du +ε1∆x +ε2∆y +ε3∆z = ∂∂ux ∆x + ∂∂uy ∆y + ∂∂uz ∆z +θ(∆
где θ(∆l) - бесконечно малая более высокого порядка по ∆l, ε1,ε2 ,ε3 → 0 при ∆x,∆y, ∆z → 0 , а ве-
личина ∆∆ul =Vcp - средняя скорость изменения ска-
лярной функции u(P) в направлении вектора l . |
x |
||||||||||||
∆u |
= |
∂u ∆x |
+ |
∂u ∆y |
+ |
∂u ∆z |
+ε |
∆x |
+ε |
∆y |
+ε |
∆z . |
|
∆l |
|
∂x ∆l |
|
∂y ∆l |
|
∂z ∆l |
|
1 ∆l |
|
2 ∆l |
|
3 ∆l |
|
=
l) ,
P1 P2  l
l
 y
y
Перейдем к пределу при |
∆ |
l |
→ |
0, что соответствует стремлению |
P →P |
: |
|
|
|
2 |
1 |
||||
|
|
|
|
|
|
|
lim |
∆u |
= ∂u cosα + |
∂u cos β + |
∂u cosγ |
, |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
∆l→0 |
∆l |
∂x |
|
|
∂y |
|
|
∂z |
|
|
|
|
|
|
|
|
||
где cosα , cos β , |
cosγ - |
направляющие косинусы вектора |
PP |
. Поскольку |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
PP |
l , то их направляющие косинусы равны. |
Так как |
l = l |
i +l |
y |
j +l |
k , то |
||||||||||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
z |
|
||
cosα = |
l |
x , cos β = |
ly |
, cosγ = |
l |
z . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
| l | |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
| l | |
|
|
|
|
l | |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Производной функции u в точке |
P(x, y, z) (обозначение |
∂u ) по направ- |
||||||||||||||||||||
О |
|
|
|||||||||||||||||||||||
|
|
|
лению вектора l |
|
называется предел lim |
∆u |
|
|
|
∂l |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
(если он существует), рав- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆l→0 |
∆l |
|
|
|
|
|
|
|
|
|
|
|
|
|
ный ∂u |
= lim |
∆u |
= ∂u cosα + ∂u cos β + |
∂u cosγ . |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
∂l |
∆l→0 |
∆l |
|
∂x |
|
|
|
∂y |
, ∂u , |
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная по направлению l |
определяет скорость изменения |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂l |
|
|
|
|
|
|
|
|
|
|
|
скалярного поля в направлении вектора l , в частности, если ∂∂ul >0, поле воз-
растает, если ∂∂ul <0, поле убывает.
Пример:
Найти производную ∂∂ul в точке Р (1,1,1) в направлении вектора
 = i + j + k , если u = x2 + y 2 + z 2 . Решение:
= i + j + k , если u = x2 + y 2 + z 2 . Решение:

Теория поля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37 |
||||||||||||
|
ux′ |
|
P = 2 x |
|
P = 2, u′y |
|
P = 2 y |
|
P = 2, uz′ |
|
P = 2 z |
|
|
|
= |
|
|
||||||||||
|
|
|
|
|
|
|
P = 2 ; |
|
3 |
, |
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
cosα = |
1 |
;cos β = |
1 |
;cosγ |
1 ; |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||
|
∂u = 2 |
|
1 |
|
|
+ 2 |
1 |
+ 2 |
1 |
|
= |
6 |
> 0 , следовательно, скалярное поле возрас- |
||||||||||||||
|
|
3 |
|
3 |
3 |
||||||||||||||||||||||
|
∂ |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
тает. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.4. Градиент скалярного поля
Пусть задано скалярное поле u = u(x,y,z).
ОГрадиентом скалярного поля u в точке P(x, y, z) называется вектор,
обозначаемый символом grad u и определяемый равенством
grad u = ∂∂ux i + ∂∂uy j + ∂∂uz k ,
5.4.1. Оператор Гамильтона (набла)
Введем символический вектор “набла” или оператор Гамильтона
= i ∂∂x + j ∂∂y +k ∂∂z = ∂∂x ; ∂∂y ; ∂∂z .
!Знак используется для записи операций векторного анализа в сокращенной и удобной для расчётов форме.
Выражение вида u(x, y, z) понимается как результат действия оператора на соответствующую функцию.
Тогда
u(x, y,z) =(i ∂∂x + j ∂∂y +k ∂∂z) u(x, y,z) =∂∂ux i +∂∂uy j +∂∂uz k =u′xi +u′y j +u′z k ,
grad u = u .
5.4.2. Связь производной по направлению с градиентом
∂∂u = ∂∂ux cosα + ∂∂uy cos β + ∂∂uz cosγ .
Пусть l0 = (cosα,cos β,cosγ ) - единичный вектор (орт) в направлении l , тогда видно, что
