Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции Соболева часть 3

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

3 Мб

Скачать

☆

<<< < Предыдущая 12 / 142 3 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

8					Лекция 1 - 4
		b	b d
		V = ∫S(x)dx = ∫ ∫		f (x, y)dy dx .
		a	a c
	Ранее было показано, что объем такого тела ра-
	вен двойному интегралу от			f (x, y) по области D,
	таким образом:
			b d
	∫∫ f (x, y)dxdy = ∫ ∫ f (x, y)dy dx .
	D		a c
	Аналогично: ∫∫ f (x, y)dxdy = ∫d dy∫b				f (x, y)dx .
		D		c a
		Запись двойного интеграла
	!	Запись двойного интеграла
	!		b d
		∫∫ f (x, y)dxdy = ∫ ∫ f (x, y)dy dx называют
		D	a c

повторным интегралом, при этом

∫cd f (x, y)dy - называют внутренним, а ∫ab{...}dx внешним интегралом. Рассмотрим произвольную область интегрирования.

ООбласть D в плоскости xOy называется правильной в направлении y или x , если каждая прямая, параллельная соответствующей координатной оси и проходящая через внутреннюю точку области, пересекает границу области в двух точках.

прав. неправ.

ТДвойной интеграл от непрерывной функции f (x, y) по правильной области D равен

двукратному интегралу от этой функции по области D .

Пусть D - правильная область в направлении Oy , ограниченная линиями: y =ϕ1(x) ,

y =ϕ2 (x) , x = a , x = b .

Тогда

	b	ϕ2 ( x)
∫∫ f (x, y)dxdy = ∫		∫ f (x,
D	a	ϕ1 ( x)

y = ϕ2 (x)

y = ϕ1 (x)

y)dy dx .

Кратные интегралы

Рассмотрение проводится аналогично предыдущему случаю; при этом площадь сечения вычисляется так:

				ϕ2 ( x)
				S(x) =		∫ f (x, y)dy ,
					ϕ1 ( x)
		b			b ϕ2 ( x)
а объем всего тела: V =		∫	S(x)dx =		∫		∫
а объем всего тела: V =			S(x)dx =					f (x, y)dy dx .
Таким образом,		a			a ϕ1 ( x)
Таким образом,
∫∫						b	ϕ2	( x)
∫∫	f (x, y)dxdy =					∫	∫
	f (x, y)dxdy =								f (x, y)dy dx .
D						a ϕ1 ( x)
Аналогично, если D -		правильная область в направлении Ox , ограни-
ченная линиями x =ψ1 ( y) ,				x =ψ2 ( y) ,			y = c,			y = d , то объем тела равен

	d	ψ2 ( y)
∫∫ f (x, y)dxdy = ∫		∫
D	c	ψ1 ( y)

f (x, y)dx dy .

!1). Правило вычисления двойных интегралов. Для того чтобы вычис-

лить двойной интеграл по произвольной правильной области D , необходимо свести его к повторному (двукратному) интегралу и проинтегрировать функцию по одной из переменных в пределах, соответствующих произвольному, но неизменному значению другой переменной, а затем результат проинтегрировать в пределах ее полного изменения.

2). Представление двойного интеграла в виде двукратного зависит от вида области D .

3). Порядок интегрирования может быть изменен в соответствии с ра-

	b	ϕ2 ( x)	d	ψ2 ( y)
венствами ∫∫ f (x, y) dxdy = ∫dx		∫	f (x, y) dy = ∫dy	∫ f (x, y) dx .
D	a	ϕ1 ( x)	c	ψ1 ( y)

4). Если область D неправильная, то ее разбивают на конечное число правильных областей Di и на основании свойств полагают, что двойной

интеграл по области D равен сумме двойных интегралов по областям Di .

5). Внешний интеграл всегда вычисляется в постоянных пределах.

6). Если пределы интегрирования в повторном интеграле от непрерывной функции конечны и постоянны, то результат не зависит от порядка интегрирования.

Пример:

10																																																				Лекция 1 - 4
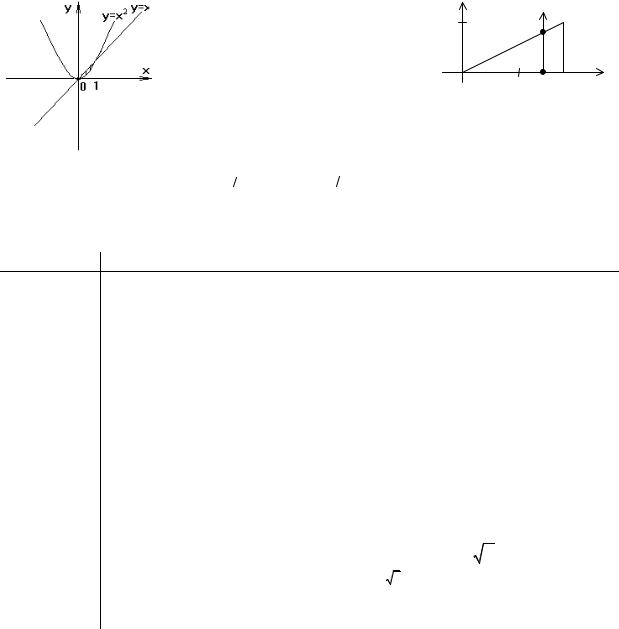
		Вычислите						∫∫xy 2 dxdy ,							если область															D			задана неравенствами:																				0 ≤ x ≤1 ,
		Вычислите						∫∫xy 2 dxdy ,							если область															D			задана неравенствами:																				0 ≤ x ≤1 ,
		−2 ≤ y ≤ 3 .						D
		−2 ≤ y ≤ 3 .
		Решение:
					2		1					3		2	1					y3				3			1		27 +8									35 x 2					1			35 1 35
					2		1					3		2	1					y3				3			1		27 +8									35 x 2					1			35 1 35
		∫∫					∫					∫			∫												∫																										или
		∫∫					∫					∫			∫					3							∫						3					3		2						3			2			6
		D	xy			dxdy =	0	xdx				−2	y dy =		0	xdx										=	0	x							dx =								0		=						=
																								−2
																								−2
					2		3		2				1		3		2				x 2				1		1	3			2					1 y3		3			1				35 35
					2		3		2				1		3		2				x 2				1		1	3			2					1 y3		3			1				35 35
		∫∫xy				dxdy = ∫y					dy∫xdx = ∫y							dy							=			∫y				dy =						=									=			.
		∫∫xy				dxdy = ∫y					dy∫xdx = ∫y							dy			2				=		2	∫y				dy =				2	3	=			2				3		=	6		.
	Пример:	D					−2						0		−2										0			−2										−2
		D					−2						0		−2										0			−2										−2



		Вычислите ∫∫x 2 ydxdy , где D																			- треугольник с																				y
								D																														1															B
		вершинами: O(0,0) , A(2,0) , B(2,1) .																																				1
		вершинами: O(0,0) , A(2,0) , B(2,1) .
		Решение:																																																			A
		Область D ,							ограниченная												прямыми:												y = 0 ,						O												x		A	x
		Область D ,							ограниченная												прямыми:												y = 0 ,						O									1			x		2	x
		y =		x		, x = 2 ,		является правильной. При фик-
		y =		2		, x = 2 ,		является правильной. При фик-
				2																									x
		сированном x									y		изменяется от 0 до																x		:
		сированном x									y		изменяется от 0 до															2			:
																												2
					2			2		2			x 2			2		2				y 2				x 2		1		2			4				1 x5		2		4
					2			2		2			x 2			2		2				y 2				x 2		1		2			4				1 x5		2		4
		∫∫x				ydxdy = ∫x						dx ∫ydy = ∫x							dx								=			∫x				dx =					=					.
		∫∫x				ydxdy = ∫x						dx ∫ydy = ∫x							dx				2			0	=	8		∫x				dx =			8 5		=			5		.
		∆OAB						0						0		0														0									0
		∆OAB						0						0		0														0									0

Пример:

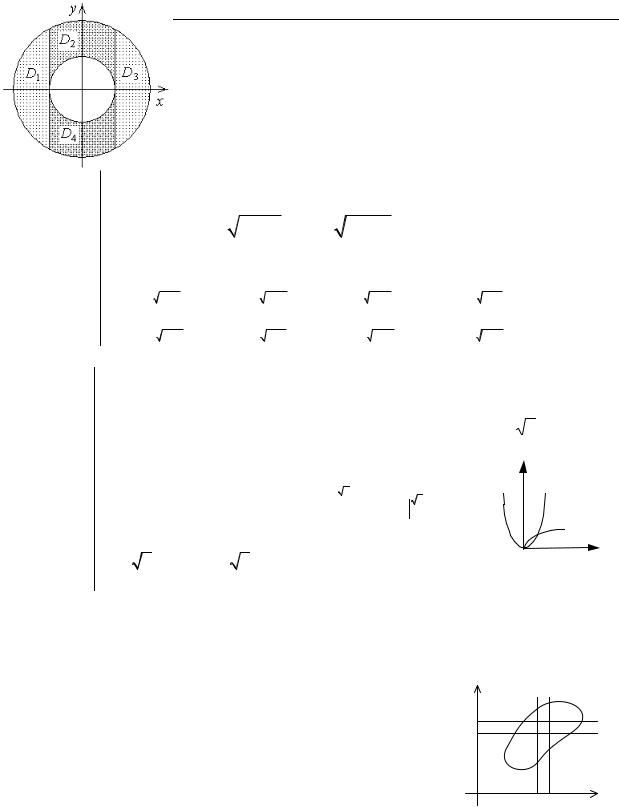
Изменить порядок интегрирования в повторном интеграле:

∫1 dx ∫x f (x, y)dy .

0 x2

Решение:

Область интегрирования D ограничена прямой y = x и параболой y = x2 и является правильной как в отношении оси Ox, так и Oy с верхней границей y = x и нижней y = x2 . Всякая пря-

мая, параллельная оси Ox, пересекает границу области не более чем в двух точках, следовательно, можно вычислить интеграл, полагая внешние пределы интегрирования y = 0, y =1.

При этом пределы во внутреннем интеграле бу-

дут иметь вид: нижний предел x1 = y , верхний x2 = + y .

Таким образом: ∫1 dx ∫x		y
Таким образом: ∫1 dx ∫x	f (x,y)dy = ∫1 dy ∫ f (x,y)dx
0 x2	0	y

Кратные интегралы

Пример:

Расставить пределы интегрирования в двойном интеграле, если область D – кольцо.

x2 + y 2 =1

D :

x2 + y 2 = 4

D – неправильная область.

Разобьем ее на четыре правильных области:

∫∫... = ∫∫... + ∫∫... +∫∫... + ∫∫....

Границами правильных областей являются дуги соответствующих ок-

ружностей y = ±

1− x2 ,

y = ± 4 − x2

и прямые x = ±1.

∫∫... = ∫∫... + ∫∫... +∫∫... + ∫∫... =

−1

4−x2

− 1−x2

= ∫dx

∫

... dy + ∫dx

∫

... dy + ∫dx

∫

... dy + ∫dx

∫

... dy.

−2

− 4−x

−1

1−x

−

4−x

−1

−

4−x

Пример:

y = x

Найти площадь фигуры, ограниченной параболами D :

= x

Решение: Полагаем f (x, y) ≡1 ;

∫∫ f (x, y)dS = ∫∫dS = ∫∫dxdy = ∫1 dx ∫x dy = ∫1 (y x2x )dx =

D		D	D	0	x2				0
= ∫1	(	x − x2 )dx = ∫1	xdx − ∫1	x2dx =	2	x23	1			1	x3	1	1

								−				=		.
					3
0		0	0				0		3			0	3

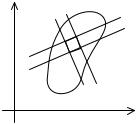
2.3.Замена переменных в двойном интеграле

Внекоторых случаях вычисление двойных интегралов значительно упрощается, если изменить область интегрирования, осуществив замену переменных в двойном интеграле.

Рассмотрим ∫∫ f (x, y)dxdy . Если координаты x

и y являются функциями новых переменных u и

D′

∆v

∆u

12	Лекция 1 - 4

x = x(u,v),

v : то каждой точке M (x, y) на плоскости xOy однозначно соот-

y = y(u,v),

ветствует точка M ′(u,v) на плоскости uOv , а числа u и v называются кри-

волинейными координатами точки M .

При этом область D отобразится в область		y	u	u + ∆u D			v + ∆v
					P3		v
′	плоскости uOv , и каждому значению		P4

D на						P2
f (x, y)	в области D соответствует то же значение
				P1

f (u,v) = f (x(u,v), y(u,v)) в области D′.

′

Разбиение области D на прямоугольные пло-

щадки приводит к разбиению области

на

P1(x1, y1 ) ,

P2 (x2 , y2 ) ,

криволинейные

четырехугольники

вершинами

P3 (x3 , y3 ) , P4 (x4 , y4 ) ,

где

x1 = x(u,v) ,

x2 = x(u + ∆u,v) ,

x3 = x(u + ∆u,v + ∆v) ,

x4 = x(u,v + ∆v) ,

y1 = y(u,v) ,

y2 = y(u + ∆u,v) ,

y3 = y(u + ∆u,v + ∆v) ,

y4 = y(u,v + ∆v) .

Заменяя приращения функций x(u,v)

и y(u,v) соответствующими диф-

ференциалами по формуле

f (u + ∆u,v + ∆v) ≈ f (u,v) + ∂f

∆v +

∂f ∆u , можно

∂v

∂u

считать, что

x = x(u,v) ,

= x(u,v) +

∂x

∆u ,

= x(u,v) +

∂x

∆u + ∂x ∆v ,

∂u

∂v

x = x(u,v) +

∂x

∆v , y = y(u,v) , y = y(x, y) +

∂y

∆u , y = y(u,v) +

∂y

∆u + ∂y ∆v ,

∂v

∂u

∂v

y = y(u,v) +

∂y

∆v . Четырехугольник при этом можно рассматривать как па-

∂v

раллелограмм. Его площадь

x3 − x4

x3 − x2

S =

[P P × P P ]

y3 − y4

y3 − y2

(x3 − x4 )( y3 − y2 ) −(x3 − x2 )( y3 − y4 )

∂x

∆u +

∂x

∆v

∂y

∆v

−

∂x

∂y

∆u +

∂y

∂u

∂v

∆v

∂u

∂v

∆v

∂x ∂y

∂x

∂y

∂x

∆u∆v −

−

∆u∆v

∂u ∂v

∆u∆v

∂u ∂v

∂v

∂u

∆u∆v

∂v

∂u ∂v

∂u

∂y ∂y

∂u

∂v

Кратные интегралы			13
	∂x	∂x
	∂x	∂x
Определитель J =	∂u	∂v	называется якобианом преобразования.
	∂y	∂y
	∂u	∂v

Предельный переход при неограниченном возрастании числа разбиений области для соответствующих интегральных сумм приводит к формуле преобразования координат в двойном интеграле:

∂x

∫∫ f (x, y)dxdy = ∫∫ f (x(u,v), y(u,v)) | J | dudv , где

J =

∂u

∂v

D′

∂y

∂u

∂v

Пример:

Вычислите ∫∫( y − x)dxdy , если область D

зада-

D′

на уравнениями y = x +1 ,

y = x − 3 ,

y = −

x + 5 .

y = −

−3

Решение:

u = y − x,

Сделаем замену переменных:

тогда область

D′

будет зада-

v = y +

ваться прямыми:

u =1, u = −3, v =

, v = 5 . Для вычисления якобиана преоб-

разования выразим x и y

через u

и v :

x = −

u +

v , y =

u +

v .

∂x

∂u

∂v

−

При

этом

J =

∫∫( y − x)dxdy =

∂y

= −

−

= −

∂u

∂v

3 3

5 1

∫∫ 4

∫∫

ududv = −8 .

u +

− −

u +

dudv

ududv =

D′

7 3−3

2.4. Двойной интеграл в полярных координатах

Перейдем в полярную систему координат

x = ρcosϕ ,

y = ρsinϕ и вы-

числим якобиан перехода: Если u =ϕ , v = ρ , x = ρcosϕ , y = ρsinϕ , то

∂x

cosϕ

−ρsinϕ

J =

∂ρ

∂ϕ

= ρcos2 ϕ + ρsin2 ϕ = ρ ,

∂y

sinϕ

ρcosϕ

∂ρ

∂ϕ

14 Лекция 1 - 4

∫∫ f (x, y)dxdy = ∫∫ f (ρcosϕ, ρsinϕ) ρd ρdϕ

D D′

2.4.1.Дифференциальный элемент площади

вполярной системе координат

Разобьем область интегрирования на элементар-

ϕi+1

ϕi

ные ячейки

∆Sij с помощью координатных линий:

ρ = ρj

окружности,

ϕ =ϕi

лучи, тогда

ρj+1

∆ρj = ρj+1 −

ρj

, ∆ϕi =ϕi+1 −ϕi . Так

как окружности

ρj

x,ρ

ортогональны радиусам, то внутренние ячейки ∆Sij с

точностью

до бесконечно

малых

более высокого

∆Sij

порядка малости относительно их площади можно

рассматривать

как прямоугольники

со сторонами

Mij

ρj ∆ϕi

и ∆ρj

, поэтому ∆Sij ≈ (ρj ∆ϕi ) ∆ρj . Ячейками

неправильной формы пренебрегаем. Переходя к пре-

x,ρ

делу, получим, что двумерный элемент площади в

полярных координатах равен dS = ρd ρdϕ .

!1). Интегрирование в полярной системе координат удобно использовать, когда область D ограничена дугами окружностей.

2). В полярных координатах внешний интеграл при сведении его к повторному может вычисляться по углам.

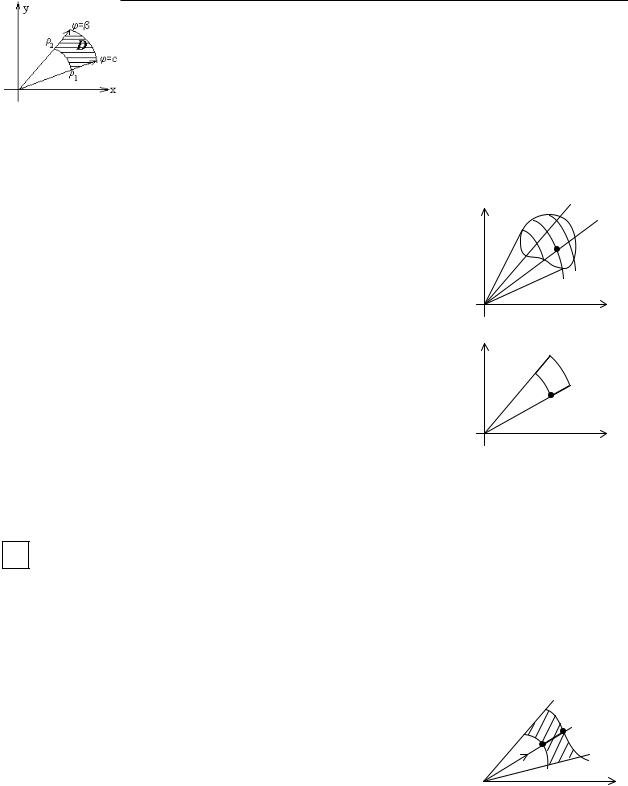
Пусть область интегрирования D определяется неравенствами: α ≤ϕ ≤ β , ρ1(ϕ) ≤ ρ ≤ ρ2 (ϕ) , где

ρ1(ϕ) и ρ2 (ϕ) - однозначные непрерывные функции на отрезке [α, β].

	ϕ = β	ϕ
	D	ϕ
		ϕ =α
	ρ1(ϕ)	ρ2 (ϕ)
0	ρ1(ϕ)	ρ
0		ρ

	β	ρ2 (ϕ)
∫∫ f (ρ,ϕ)ρd ρdϕ =∫dϕ ∫ f (ρ,ϕ)ρd ρ .
D	α	ρ1 (ϕ)

3). В полярных координатах внешний интеграл может вычисляться и по полярному радиусу. Пусть область интегрирования D определяется не-

Кратные интегралы

равенствами: R1 ≤ ρ ≤ R2 ,	ϕ1(ρ) ≤ϕ ≤ϕ2 (ρ) , где ϕ1(ρ) и ϕ2 (ρ) - одно-
значные непрерывные функции на отрезке [R1, R2 ] .
	R2	ϕ2 ( ρ)
∫∫ f (ρ,ϕ)ρd ρdϕ =∫ ρd ρ		∫ f (ρ,ϕ)dϕ .
D	R1	ϕ1 ( ρ)

Пример:

Записать в полярных координатах двойной интеграл по области D:

+ y

- кольцо.

+ y

= 4

Решение: полярные координаты

x = ρ cosϕ, y = ρsinϕ .

ρ2 cos2 ϕ + ρ2 sin2 ϕ =1,

ρ2 =1, ρ =1,

аналогично ρ2 = 2 .

Область интегрирования в полярных координа-

′

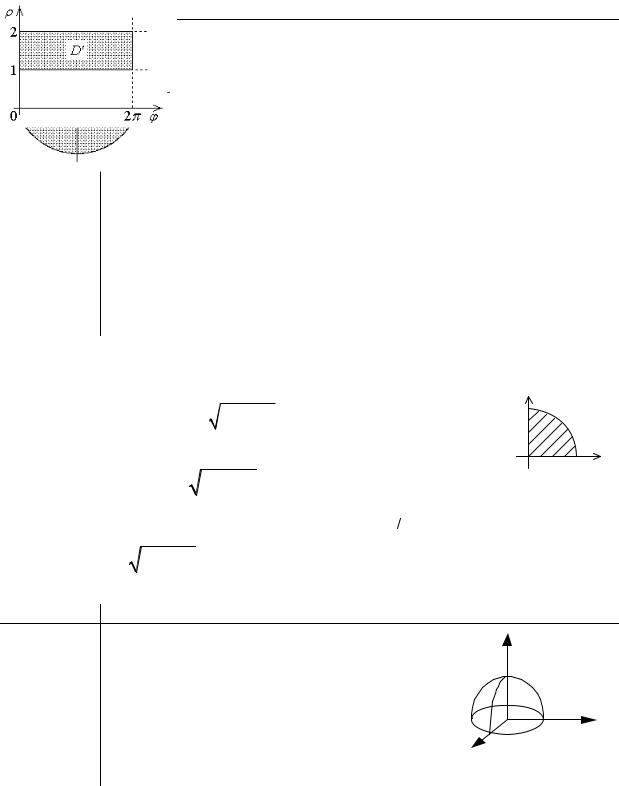
тах D — прямоугольник: 1 ≤ ρ ≤ 2, 0 ≤ϕ ≤ 2π .

∫∫ f (x, y)dxdy = ∫∫ f ′(ρ,ϕ)ρd ρdϕ =

D′

2π

ρ=2

= ∫ dϕ ∫ f ′(ρ,ϕ)ρ d ρ .

Пример:

ρ=1

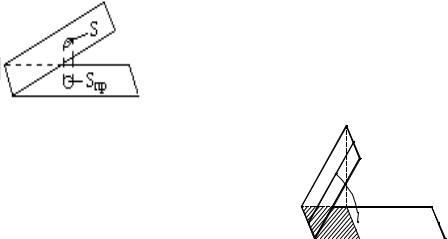
Вычислите ∫∫

dxdy

, где D - первая четверть круга

+ y

R =1 с центром в точке O (0,0).

x2 + y2 , D : 0 ≤ϕ ≤ π

ρ =

, 0 ≤ ρ ≤1.

dxdy

ρd ρdϕ

π 2

π .

∫∫

= ∫∫

=∫∫d ρdϕ = ∫

dϕ∫d ρ =

1 =

x + y

Пример:

Найти объем тела, если оно задается поверх-

z =1 − x2 − y2 ;

ностями: z = 0.

Решение:

Область интегрирования – проекция фигуры на плоскость xOy . Граница D: x2 + y 2 =1 - окружность.

Лекция 1 - 4

Перейдем в полярную систему координат: D′:

≤ ϕ ≤

2π

V = ∫∫ f (x, y)dxdy = ∫∫(1 − x2

− y 2 )dxdy =

= ∫∫(1−r2 )rdrdϕ =

2∫π dϕ∫1

(1−r2 )rdr =

D′

0 0

2π

= ∫dϕ(

−

)

= ∫ dϕ(

−

) =

0 =

3. Поверхностный интеграл первого типа (рода)

Поверхностные интегралы первого типа – это обобщение двойных интегралов по области D . Рассмотрим фигуру, которая является поверхностью ∑ ; Φ → Σ. Интеграл по фигуре в данном случае является поверхностным

интегралом первого рода от функции f (P) = f (x, y, z) по поверхности ∑ :

∫∫		n
∫∫		rn →0 i=1
	f (x, y, z)dσ =lim Σ f (Pi )∆σi
∑
3.1. Вычисление поверхностных интегралов первого рода
Вычислим ∫∫ f (x, y, z)dσ . Пусть		f (x, y, z)≥ 0 , а поверхность Σ задана
Σ

уравнением z = f (x, y).

Лемма. Площадь проекции плоского участка одной плоскости P1 на другуюP2 равна площади самого участка, ум-

ноженной на модуль косинуса двугранного угла между плоскостями: Sпр = S cosϕ .

Доказательство:

S = l a ; Sпр = a l

cosϕ

= S

cosϕ

(поскольку Sпр ≥ 0 ,

косинус берется по модулю).

Пусть требуется вычислить поверхностный инте-

грал первого рода по поверхности Σ. Область D являет-

ся проекцией поверхности Σ на плоскость xOy . Через

точку поверхности

A(x, y, z ) проведем касательную плоскость. Ее уравне-

ние: z − z = ∂z (x − x )+ ∂z (y − y ).

Выберем часть поверхности dσ и спроек-

∂x

∂y

тируем ее на касательную плоскость. Обозначим проекцию dσ. Будем считать dσ ~ dσ . Обозначим n - нормаль к касательной плоскости:

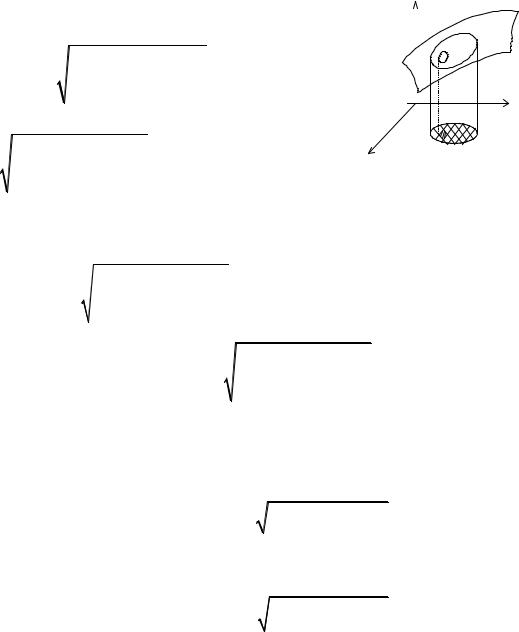
Кратные интегралы						17
	∂z	,	∂z		. Поскольку k (0,0,1)- нормаль к xOy , то угол ϕ	- угол между
n				,−1
	∂x		∂y

касательной плоскостью и плоскостью Oxy равен углу между векторами n и

k .

Найдем связь между dS (проекцией dσ на плоскость xOy ) и dσ

(n,k )

−1

cosϕ =

;

z = f (x,y)

1 +

∂z

∂x

∂y

cosϕ

; в пределе при

∂z

∂x

∂y

r → 0,

dσ = dσ,

dS = dσ

cosϕ

dσ =

;

cosϕ

dσ = dS

∂z 2

1 +

;

∂x

∂y

∫∫

f (x, y, z)dσ

∫∫

(

x, y, z (x, y) dS

1 +

∂z 2

∂z 2 .

)

∂x

∂y

Так записывается поверхностный интеграл, если поверхность задана уравнением z = z (x, y).

Если поверхность задана уравнением y = y(x, z), то

∫∫ (

)

∫∫ (

( ) )

( x )

( z )

f x, y, z dσ =

f x, y x, z , z

′

dS .

Dxz

Аналогично, если x = x(y, z), то

∫∫ f (x, y, z)dσ = ∫∫ f (x(y, z), y, z) 1+ (x′y )2 + (x′z )2 dS ,

Σ Dyz

где Dxz , Dyz - проекции Σ на плоскости Oxz, Oyz .

<<< < Предыдущая 12 / 142 3 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.2019861 Кб136Лекции РИМ сводная_1.doc
#
17.11.2019236 Кб13Лекции РЦБ - кусочки.doc
#
21.12.2018682 Кб62Лекции сенсоры.doc
#
24.08.2019643 Кб54Лекции сенсоры.doc
#
23.02.2015732 Кб18лекции сист эл снабж.pdf
#
23.02.20153 Мб81Лекции Соболева часть 3.pdf
#
22.02.20151 Мб377Лекции соц психология.doc
#
23.02.20155 Мб111Лекции Стечкина по матану.pdf
#
01.05.20252 Мб5Лекции ТОМ 7.12.07doc.doc
#
21.12.201816 Мб64Лекции ТЭПП.doc
#
01.04.20253 Мб6ЛЕКЦИИ УПРАВЛЕНИЕ ДАННЫМИ 2012.doc