
electrodynamics
.pdf
§11. Уравнения Максвелла |
|
201 |
|||||||||||
|
dϕ |
= 2 |
|
|
ϕ 1 / 4 (x) . |
|
(11.19) |
|
|||||
|
a |
|
|
||||||||||
|
|
|
|
||||||||||
|
dx |
|
|
|
|
|
|
|
|||||
Интегрируя (11.19), получаем |
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||
ϕ (x) = ( |
3 a |
x) |
4 3 + C |
|
. |
|
|||||||
|
1 |
|
|||||||||||
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
Константу C1 находим из условия ϕ (0) = 0 : C1 = 0 , откуда |
|||||||||||||
ϕ (x) = ( |
9a |
) |
2 3 x |
4 3 . |
|
(11.20) |
|
||||||
|
|
|
|||||||||||
4 |
|
|
|
|
|
|
|
|
|
||||
Здесь а неизвестная пока постоянная. Найдем ее из граничного условия на аноде: ϕ(d) = U0. Подстановка в (11.20) найденного значения а дает окончательно:
ϕ ( x) = U |
|
( x |
|
4 |
|
0 |
d |
) 3 . |
(11.21) |
||
|
|
|
|
202 |
|
|
|
|
§11. Уравнения Максвелла |
|||||
|
|
|
|
|
|
|||||
|
Пример |
11.3. |
Плоский |
конденсатор, |
||||||
|
представляющий собой две круглые пластины |
|||||||||
|
радиусом |
R , |
заряжают постоянным |
током |
I , |
|||||
|
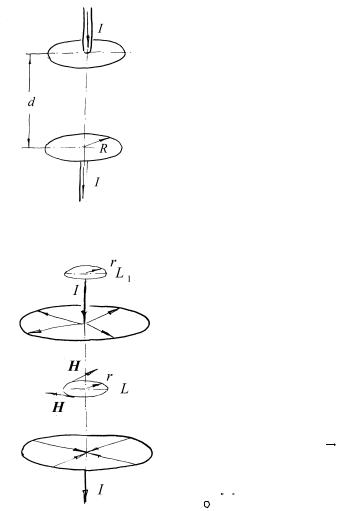
направление которого показано на рис.11.3. |
|||||||||
|
Определите напряженность |
магнитного поля |
H , |
|||||||
|
возникающего в зазоре между пластинами |
|||||||||
|
конденсатора в |
зависимости |
от |
расстояния |
r |
от |
||||
|
оси |
конденсатора. |
Сравните |
полученное |
||||||
|
выражение с формулой для напряженности поля |
|||||||||
|
H вне конденсатора. Чем можно объяснить скачок |
|||||||||
|
напряженности |
поля |
H |
при |
переходе |
через |
||||
Рис.11.3 |
поверхность пластины конденсатора? |
|
|
|
||||||
Решение. Так как распределение тока проводимости вне пластин и токов смещения между ними обладает цилиндрической симметрией, воспользуемся этим фактом при выборе контура обхода для теоремы о циркуляции (см. рис.11.4). В силу симметрии модуль напряженности магнитного поля на окружности L , ось которой совпадает с током, одинаков во всех точках, поэтому
циркуляция вектора H |
по такому контура |
равна |
|
∫H dl = 2πrH . |
(11.22) |
L |
|
Рис.11.4

§11. Уравнения Максвелла |
203 |
Для контура, лежащего внутри конденсатора, как следует из уравнения (11.1), ее следует приравнять току смещения, пронизывающему контур L :
I |
|
= |
∂ |
|
DdS = |
∂ |
(πr 2 D)= πr 2 |
∂ |
σ = |
r 2 |
|
∂ |
Q = |
r 2 |
I . (11.23) |
|
см |
∂t ∫ |
|
|
|
|
|
||||||||||
|
|
|
|
∂t |
∂t |
|
R 2 ∂t |
|
R 2 |
|
||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
Из этого условия находим поле: |
|
|
|
|
|
|
|
|
||||||||
H = |
|
r |
I . |
|
|
|
|
|
|
|
(11.24) |
|||||
|
|
|
|
|
|
|
|
|||||||||
2πR 2 |
|
|
|
|
|
|
|
|||||||||
Для определения поля вне конденсатора применим теорему о циркуляции к контуру L1 (рис.11.4). Циркуляцию вектора H по этому контуру следует приравнять току проводимости I , заряжающему конденсатор, откуда
I
H 1 = π . (11.25) 2 r
Скачок поля при переходе через пластину конденсатора обусловлен наличием радиальных токов, текущих по поверхности пластин в процессе зарядки конденсатора (рис.11.4).
Пример 11.4. Заряженный и отключенный от источника плоский конденсатор с круглыми пластинами медленно разряжается объемными токами проводимости, возникающими в диэлектрике между обкладками из-за наличия слабой проводимости. Пренебрегая краевыми эффектами, вычислите напряженность магнитного поля внутри конденсатора.
Решение. Воспользуемся цилиндрической симметрией в распределении токов и вычислим циркуляцию вектора Н для контура L , введенного в предыдущем примере:

204 |
§11. Уравнения Максвелла |
|
|
|
|
|
|
∂ |
|
|
|
∂σ |
|
2πrH = ∫ j + |
|
D dS = ∫ j + |
dS . |
(11.26) |
|||
|
|||||||
S |
|
∂t |
|
S |
|
∂t |
|
|
|
|
|
|
|
||
В силу закона сохранения заряда выражение в круглых скобках в правой части (11.26) равно нулю, следовательно равна нулю и напряженность поля H .
Пример 11.5. Заряженный и отключенный от источника плоский конденсатор с круглыми пластинами радиусом R пробивается электрической искрой вдоль своей оси. Считая разряд квазистационарным и пренебрегая краевыми эффектами, вычислите мгновенное значение напряженности магнитного поля H внутри конденсатора как функцию расстояния r от его оси, если сила тока в электрической искре в рассматриваемый момент времени равна I .
Решение. Как и в предыдущей задаче, воспользуемся симметрией в распределении токов и выберем контур L в виде окружности, плоскость которой параллельна пластинам, а ее центр совпадает с осью симметрии
пластин, вдоль которой протекает ток. На этом контуре модуль вектора H в
силу симметрии остается неизменным, поэтому ∫H dl = 2πrH . Контур L
L
пронизывает ток проводимости I , текущий в искре, и ток смещения, текущий в противоположную сторону и подсчитанный ранее в Примере 3 (11.23).
Подставляя эти токи в выражение для циркуляции H получаем:
2πrH = I − |
r 2 |
|
I , |
|||||
R 2 |
||||||||
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
I |
|
|
r |
2 |
|
||
H = |
1 |
− |
|
. |
||||
|
|
2 |
||||||
|
|
|
|
R |
|
|||
|
2πr |
|
|
|
||||
§11. Уравнения Максвелла |
205 |
В отличие от предыдущего примера, теперь ток проводимости не распределен равномерно по объему поля между пластинами, а сосредоточен в узкой области вблизи оси конденсатора.
Пример 11.6. Обкладки плоского конденсатора имеют форму дисков радиусом R =10см. Пространство между обкладками заполнено однородным диэлектриком с диэлектрической и магнитной проницаемостями ε и µ .
Конденсатор включен в цепь переменного тока I = I 0 cos ωt . Пренебрегая краевыми эффектами, вычислите электрическую и магнитные энергии, локализованные в конденсаторе. Найдите отношение максимальной магнитной к максимальной электрической энергии. При расчетах следует принять
ε = µ = 1 , а частоту тока ν = ω 2π =100 Гц.
2π =100 Гц.
Решение. Энергия электрического поля, заключенного между обкладками плоского конденсатора определяется выражением (5.8) и для данных задачи равна
W |
|
= |
Q 2 |
= |
Q 2 d |
. |
(11.27) |
эл |
|
|
|||||
|
|
2C |
|
2εε 0πR 2 |
|
||
|
|
|
|
|
|||
Магнитное поле в конденсаторе создается током смещения. Оно было подсчитано в Примере 3 и задается выражением (11.24). Плотность энергии магнитного поля задается выражением (9.9). Воспользуемся ею для определения энергии магнитного поля в конденсаторе. Энергия поля в цилиндрическом слое, ограниченном радиусами r и r + dr равна
dW |
|
= |
1 |
µµ |
|
H 2 dV = µµ |
|
2d rdr |
|
I |
2 r |
2 |
. |
(11.28) |
маг |
|
0 |
0 |
|
|
|
|
|
||||||
|
|
2 |
|
|
2 |
|
4π 2 R 4 |
|
||||||
|
|
|
|
|
|
|
|
|
||||||
Интегрируя это выражение по всему объему цилиндра, получаем
206 |
|
|
|
|
|
|
|
|
|
|
|
|
§11. Уравнения Максвелла |
|
|
|
|
µµ |
|
dI 2 |
R |
|
µµ |
|
dI 2 |
|
|
||
|
|
= |
0 |
|
r 3 dr = |
0 |
|
|
||||||
W |
|
|
|
|
|
|
|
. |
(11.29) |
|
||||
маг |
|
|
|
4 ∫ |
|
|
|
|
||||||
|
|
4π |
2 R |
|
16π 2 |
|
|
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Подставим в выражения (11.27) и (11.29) заданное по условию задачи
выражение для тока и для заряда Q = ∫ I (t )dt = |
I 0 |
sin ωt |
и найдем отношение их |
|||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
максимальных значений |
|
|
|
|
|
|
||||||||
k = |
W m |
маг |
= |
µµ |
0 |
εε 0ω 2 R 2 |
. |
|
|
|
||||
W m |
элек |
|
|
|
|
8π |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
Учитывая, что |
скорость |
электромагнитных |
волн в |
вакууме определяется |
||||||||||
выражением c 2 |
= |
|
1 |
|
, |
|
перепишем найденное отношение в окончательном |
|||||||
|
|
|
|
|
||||||||||
ε 0 |
µ 0 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = |
µεω 2 R 2 |
|
= 0,5 10 −14 . |
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||
|
8πc 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Видим, что энергия магнитного поля составляет ничтожную долю от энергии электрического поля, заключенного между обкладками конденсатора.
Пример |
11.7. Пространство внутри длинного соленоида, состоящего из |
N витков |
проволоки, заполнено однородным веществом с диэлектрической |
проницаемостью ε и магнитной проницаемостью µ . Длина соленоида равна l ,
радиус R . По обмотке соленоида течет переменный ток I = I 0 cos ωt .
Пренебрегая краевыми эффектами, вычислите электрическую и магнитную энергии, локализованные внутри соленоида, и найдите отношение максимальных значений этих энергий. Численный расчет провести для R = 5 см,
ε = µ = 1 при частоте тока ν = ω 2π =100 Гц.
2π =100 Гц.

§11. Уравнения Максвелла |
207 |
Решение. Энергия магнитного поля, заключенного в катушке, определяется выражением (9.7), а ее индуктивность – формулой (9.15):
|
|
= |
1 |
|
2 = |
µµ |
0 |
N 2πR 2 |
2 |
cos 2 ωt . |
(11.30) |
|
W |
|
|
LI |
|
|
I |
||||||
маг |
|
|
|
|
0 |
|||||||
|
|
2 |
|
|
|
|
2l |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
Для определения электрического поля в катушке отметим, что распределение тока обладает цилиндрической симметрией, поэтому силовые линии напряженности электрического поля будут окружностями, концентрическими с витками катушки. Выберем контур C , совпадающим с одной из силовых линий и запишем для него закон электромагнитной индукции:
∫E dl = − |
∂ |
∫ BdS . |
(11.31) |
|
∂t |
||||
C |
S |
|
||
|
|
Индукция магнитного поля на оси соленоида задается выражением (9.13). Подставляя его в (11.31), получаем
|
|
∂ |
|
|
|
|
N |
2 |
|
|
µµ |
0 |
ωNπr 2 |
|
|
|||
2πrE = − |
|
|
|
µµ |
|
|
I (t )πr |
|
= |
|
|
I |
|
sin ωt , |
||||
∂t |
0 |
|
|
|
|
|
0 |
|||||||||||
|
|
|
|
|
l |
|
|
|
|
|
l |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E(r ) = |
µµ 0ωNr |
I 0 sin ωt . |
|
|
|
|
|
|
|
|
(11.32) |
|||||||
|
2l |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Энергия электрического поля, заключенная в катушке, может быть подсчитана
через плотность энергии |
(5.9). Выберем цилиндрический слой |
между |
цилиндрами с радиусами r |
и r + dr , тогда энергия электрического поля в этом |
|
слое будет равна |
|
|
|
|
|
1 |
|
|
|
εε |
0 |
µ 2 µ |
2ω 2 N 2 |
|
2 |
|
dW |
|
= |
|
εε |
|
E 2 dV = |
|
|
0 |
r 2 I |
sin 2 ωt 2πrdrl . |
||
элек |
2 |
0 |
|
|
8l 2 |
0 |
|||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||

208 |
|
|
|
§11. Уравнения Максвелла |
|||
Интегрируя по всей катушке, окончательно получим |
|
|
|||||
|
|
εε 0 µ 2 µ 02ω 2 N 2π |
R |
εε 0 µ 2 µ 02ω 2 N 2πR 4 |
|
|
|
Wэлек |
= |
I 02 sin 2 ωt ∫r 3 dr = |
I 02 sin 2 ωt . |
||||
4l |
16l |
||||||
|
|
0 |
|
|
|||
|
|
|
|
|
|
||
Отношение максимальных значений электрической энергии к энергии магнитного поля равно
k = |
W |
элек |
= |
|
µµ |
0 |
εε |
0 |
ω 2 R 2 |
||||
|
|
|
|
|
. |
||||||||
W магн |
|
|
|
|
|
8 |
|||||||
|
|
|
|
|
|
|
|
|
|||||
Учитывая, что |
скорость |
электромагнитных волн в вакууме определяется |
|||||||||||
выражением |
c 2 |
= |
|
|
1 |
|
|
, |
перепишем найденное отношение в окончательном |
||||
|
|
|
|
|
|
||||||||
|
ε 0 |
µ 0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
k = |
µεω 2 R 2 |
|
= 1,3 10 −15 . |
||||||||||
|
|
||||||||||||
|
|
8c 2 |
|
|
|
|
|
|
|
|
|
|
|
Пример 11.8. Внутри цилиндрической области пространства радиусом R=10 см (см. рис.11.5) магнитное поле направлено параллельно оси OO′ воображаемого цилиндра, а его индукция изменяется по закону B(t) = k t, k=60 Тл/c. Вне этой области магнитная индукция равна нулю. На расстоянии a=19 см от оси OO′ расположена,
как показано на рисунке, тонкая проводящая палочка длиной l=22 см. Найдите разность потенциалов между концами палочки.
Решение. Как внутри, так и вне области,

§11. Уравнения Максвелла |
209 |
занятой переменным во времени магнитным полем, существует электрическое поле, определяемое уравнением (11.2). Структура этого поля внутри области однородного цилиндрически симметричного магнитного поля была подробно рассмотрена в примере 1. Как было показано, в рассматриваемом случае отлична от нуля только азимутальная составляющая Еϕ , и она равна –½ kr (r< R). Найдем теперь электрическое поле вне области магнитного поля. При r>R
∂(rEϕ ) =
(В=0) эта составляющая удовлетворяет уравнению 0 , откуда следует
∂r
Еϕ = C/r. Теперь особая точка r = 0 не входит в расматриваемую область, и это решение не должно быть отброшено. Постоянная С находится из условия
непрерывности вектора E при r = R: C/R = −½kR, откуда окончательно:
Eϕ |
= − |
kR 2 |
(11.33) |
|
2r |
||||
|
|
|
Заметим, что найденное выражение для вихревого электрического поля есть не
что иное как производная − |
∂A |
в формуле (11.13) и могло быть легко получено |
|
||
|
∂t |
|
из выражения для векторного потенциала. При помещении проводящей палочки во внешнее поле в ней произойдет перемещение свободных зарядов и их стационарное распределение должно удовлетворять условию равенства нулю полного электрического поля:
|
|
|
r |
|
|
|
|
|
r |
|
r |
|
|
∂A |
r |
|
r |
|
|
∂A |
|
E |
= − gradϕ |
− |
= 0 , откуда следует gradϕ = −E |
|
, где E |
|
= − |
− поле |
||
∂t |
i |
i |
∂t |
|||||||
|
|
|
|
|
|
|
|
|
электромагнитной индукции.
Интегриуя это выржение вдоль палочки, получим выражение для искомой разности потенциалов:
ϕ = |
1 |
kR 2α , |
(11.34) |
|
|||
2 |
|
|
|

210 §11. Уравнения Максвелла
где α − угол, под которым видны концы палочки из центра |
области магнитного |
||||
поля. В рассматриваемой геометрии α = 2 arcsin |
|
l |
|
|
. Отметим, что |
|
|
|
|
||
|
|
|
|
||
|
|
||||
 4a 2 + l 2
4a 2 + l 2
рассчитанная разность потенциалов учитывает только потенциальную часть полного поля и, поэтому, не равна работе по перемещению пробного заряда от одного конца палочки до другого. Эта работа зависит от траектории (так как полное поле не потенциально), и включает как работу потенциальных сил, так и вихревой составляющей поля.
Окончательно, ϕ = kR 2 arcsin |
|
l |
В. |
||
|
|
|
=0,314 |
||
|
|
|
|||
|
|||||
|
|
4a 2 + l 2 |
|
||
Задание для самостоятельной работы
11.1. Из материала с проводимостью λ=6 107 (Ом м)-1 изготовлен сплошной цилиндр длиной l=4 см и радиусом R=1 см. Цилиндр помещают в
нестационарное магнитное поле, вектор индукции которого B параллелен оси цилиндра. Магнитное поле изменяется по закону
k t, |
0 ≤ r ≤ R1 , |
B(t) = |
r > R1 , |
0, |
где r – расстояние от оси цилиндра, а R1>R. Найдите тепловую мощность, выделяющуюся в цилиндре за счет токов Фуко, если k=10 Тл/c.
