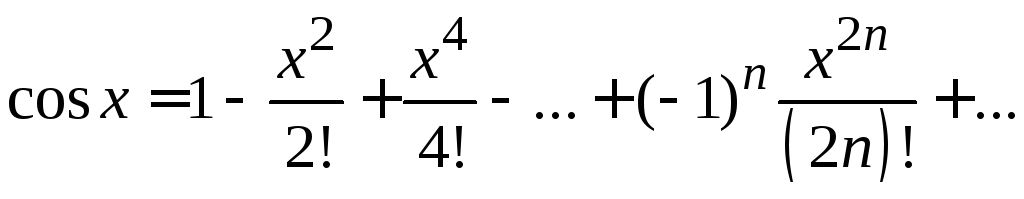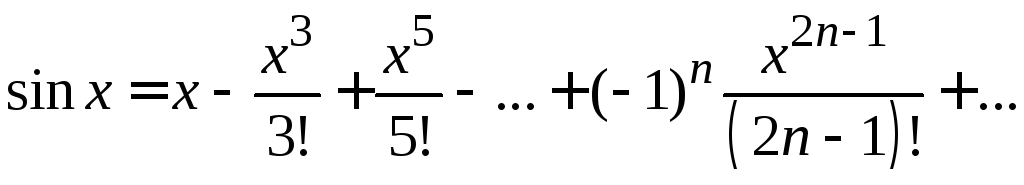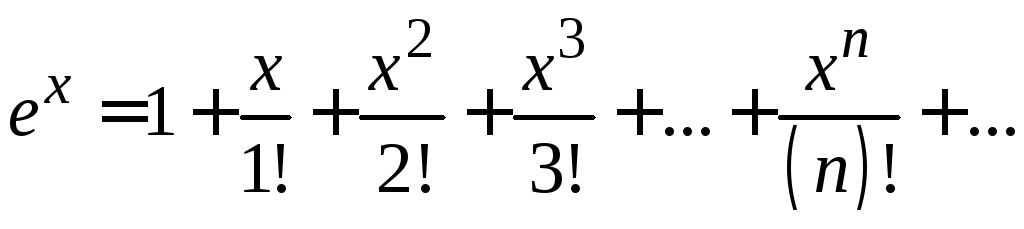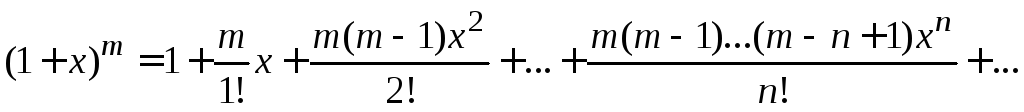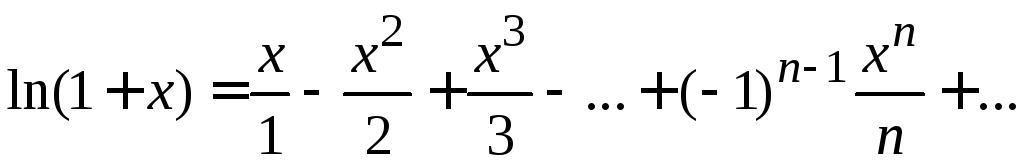Методические указания и примеры выполнения заданий

Пример 1. Проверить, выполняется ли необходимое условие сходимости для ряда

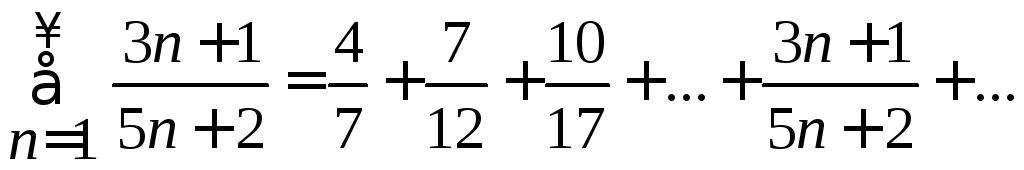
Решение.

При - получим

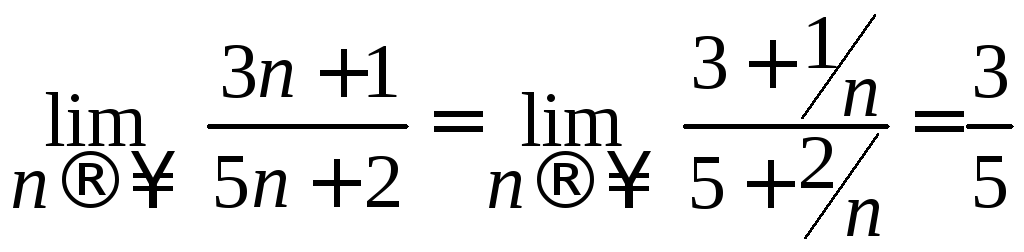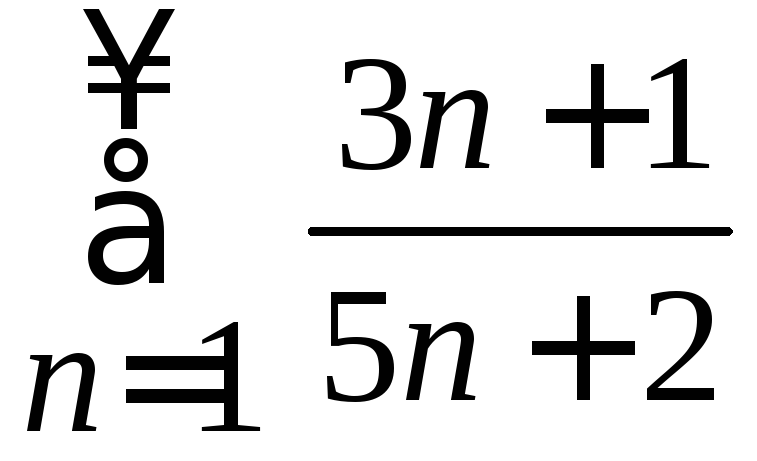, т.е. рядрасходиться, так как не выполнен необходимый признак.

Ответ: ряд расходится.

Пример 2. Пользуясь признаком сравнения определить сходимость (расходимость) ряда .

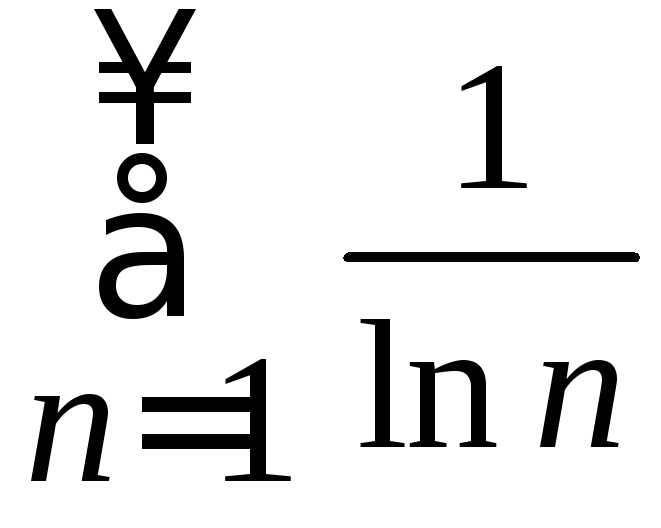Решение. Ряд

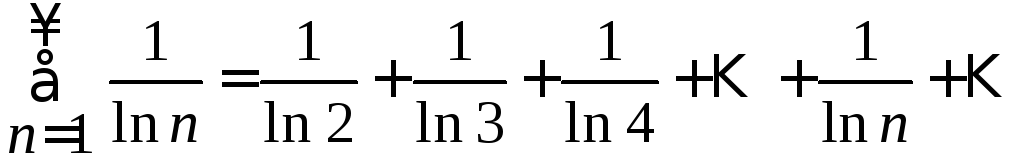
Сравним его с гармоническим рядом 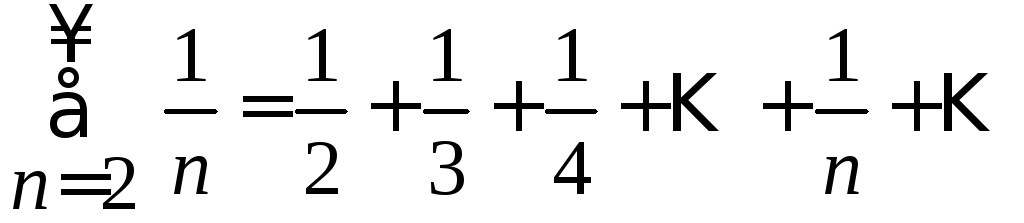, который является расходящимся. Т.к.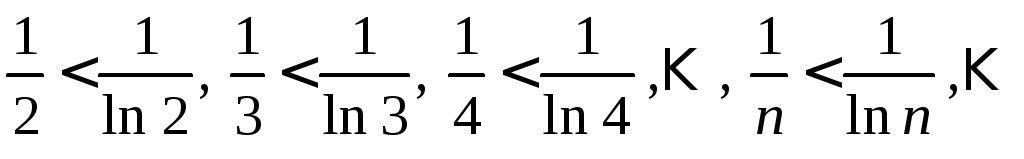, то по признаку сравнения ряд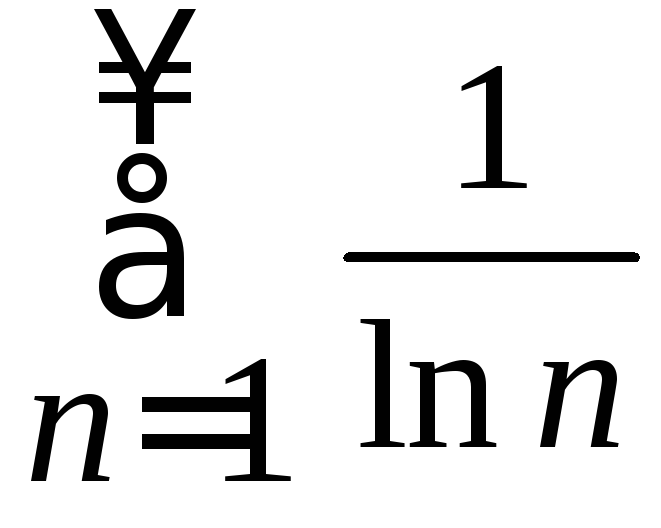расходится.

Ответ:.ряд расходится по признаку сравнения.

Пример 3. Исследовать сходимость числового ряда .

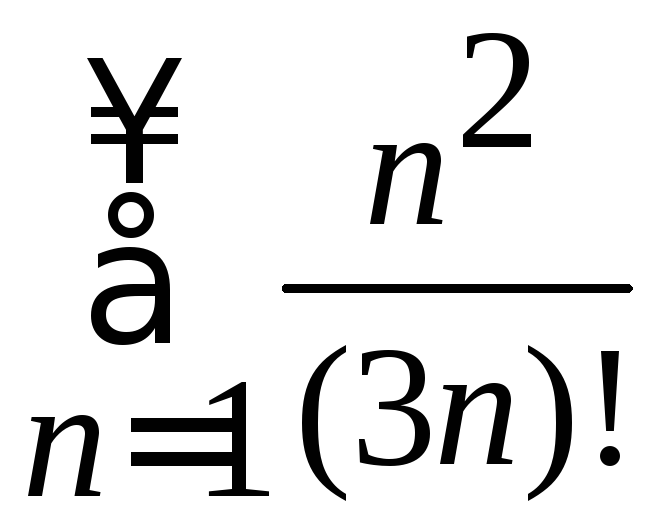Решение. Имеем 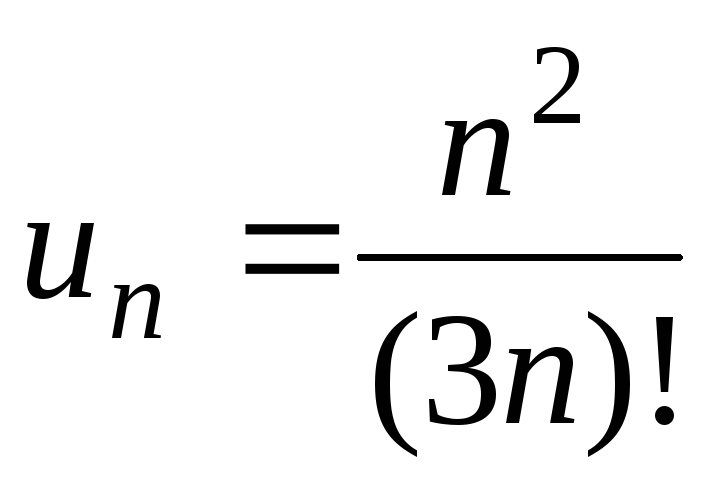,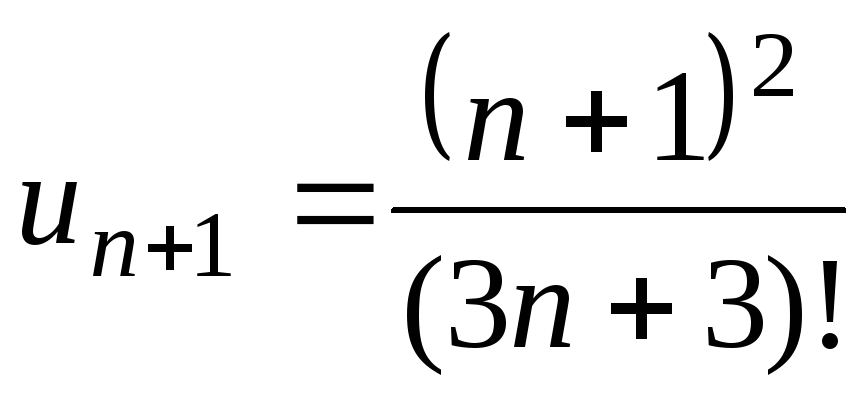. Применяя признак Даламбера, вычислим

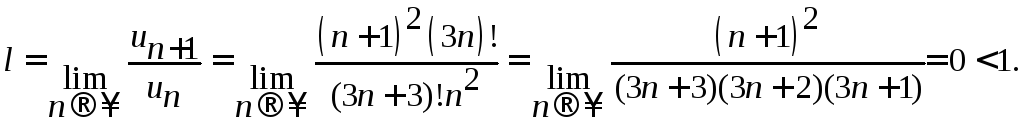
Ответ: По признаку Даламбера данный ряд сходится.

Пример 4. Исследовать сходимость числового ряда .

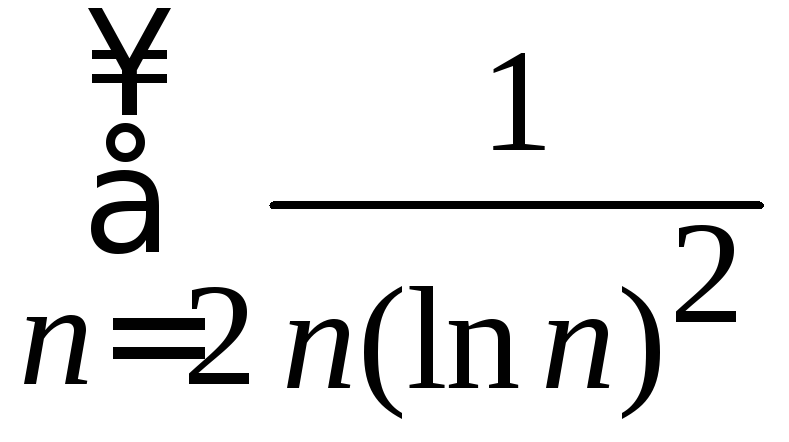Решение. Введем функцию 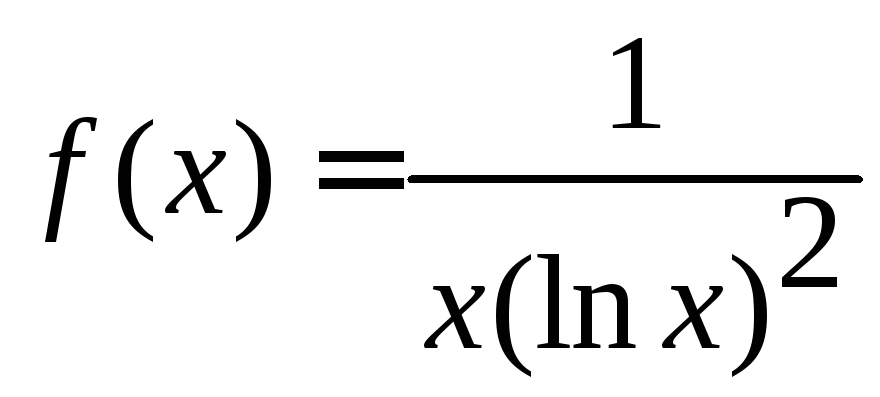, удовлетворяющую условиям, и исследуем сходимость по интегральному признаку. Для этого вычислим

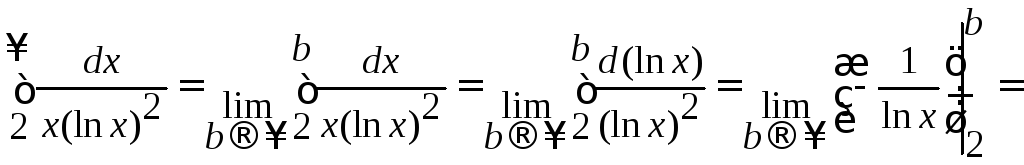
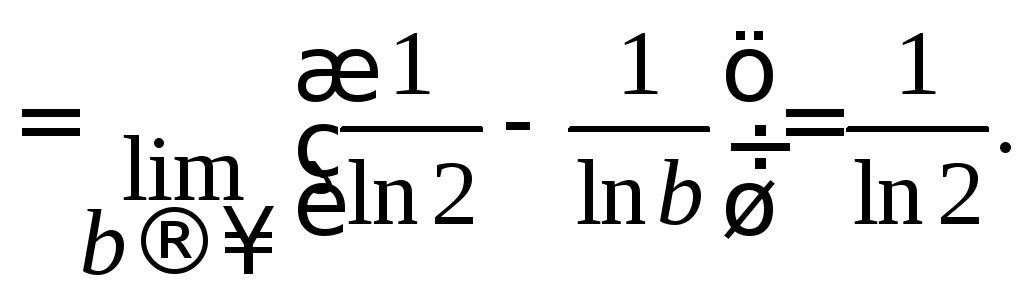
Несобственный интеграл сходится, следовательно, сходится и данный ряд.

Ответ: ряд сходится по интегральному признаку.

Пример 5. По признаку Лейбница определить сходимость знакопеременного ряда .

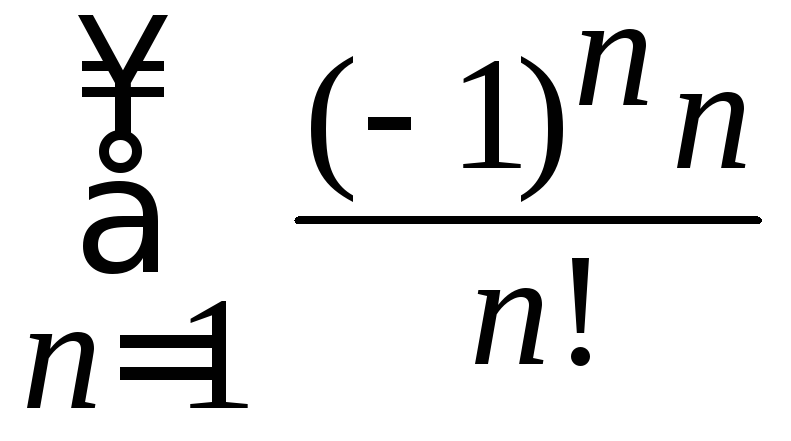Решение

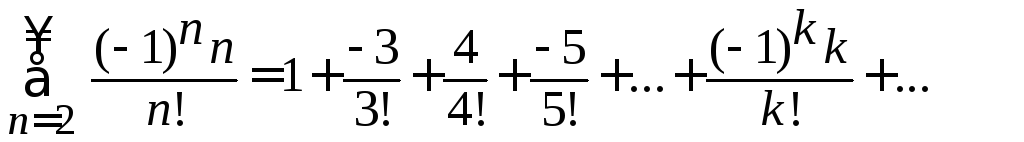Общий член ряда имеет вид .

Проверим условия теоремы Лейбница.

1) Члены ряда по абсолютной величине убывают:

2) Общий член ряда стремится к нулю

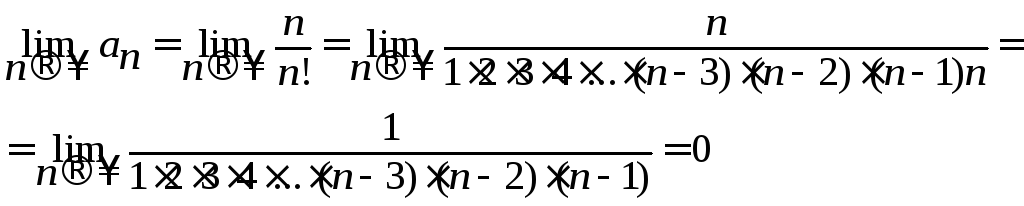
Рассмотрим ряд, составленный из абсолютных величин . Применим признак Даламбера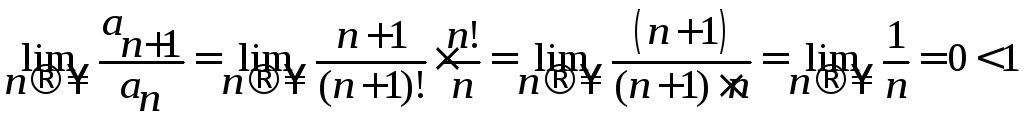, следовательно ряд сходится абсолютно.

Ответ: ряд сходится по признаку Лейбница.

Пример 6. Найти интервал сходимости степенного ряда .

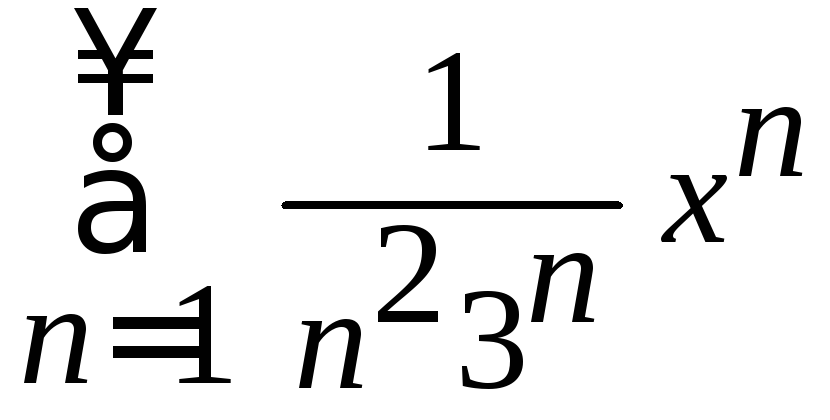Решение

Составим ряд из модулей членов ряда 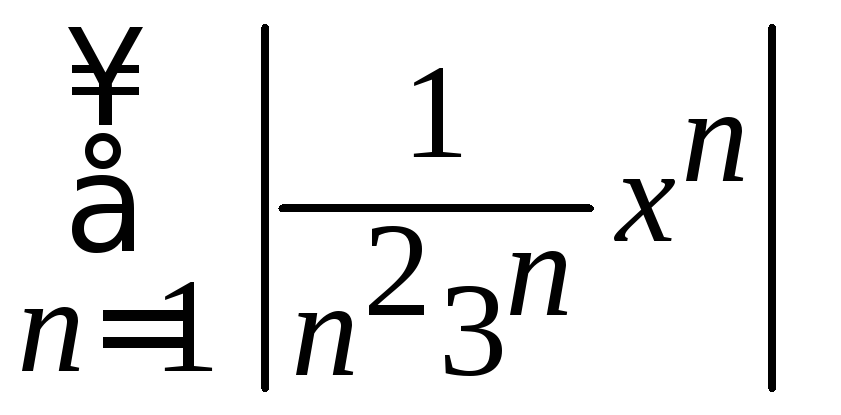и вычислим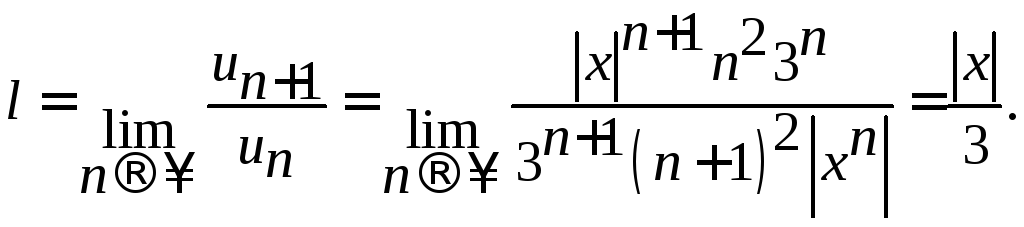

По признаку Даламбера ряд сходится при , отсюдаили. Следовательно, ряд абсолютно сходится при.

Исследуем сходимость ряда в граничных точках.

При ииз данного ряда получаем соответственно числовые ряды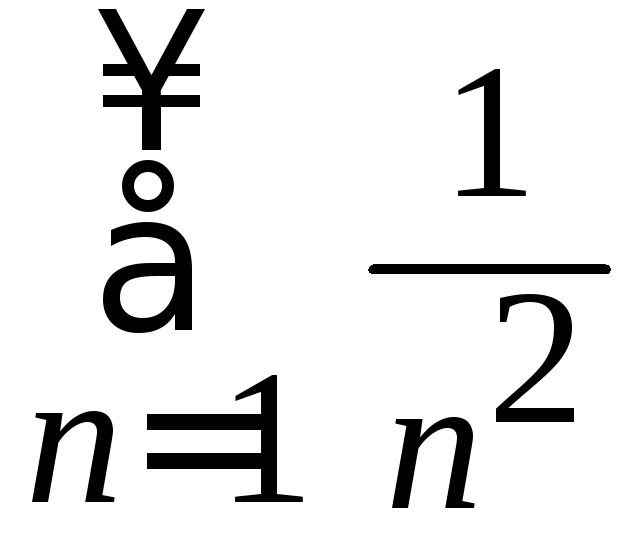и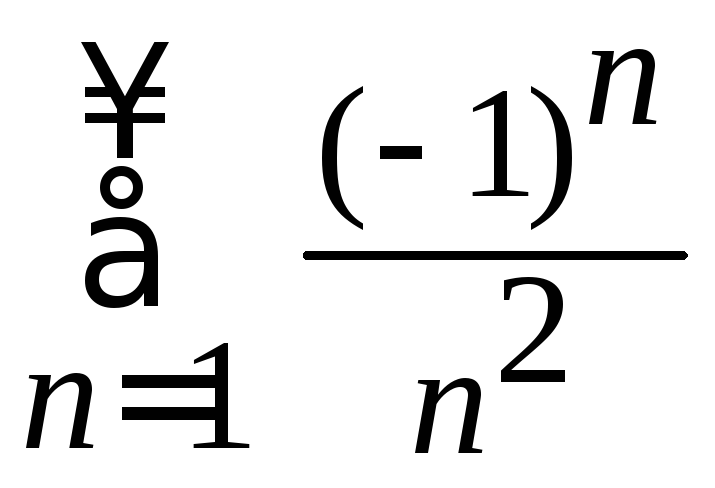. Из интегрального признака сходимости следует, что эти ряды сходятся абсолютно, поэтому интервалом сходимости данного ряда является промежуток.

Ответ: ряд сходится внутри промежутка .

Пример 7. Вычислить приближенно с указанной степенью точности

Решение

Представим Вычислим

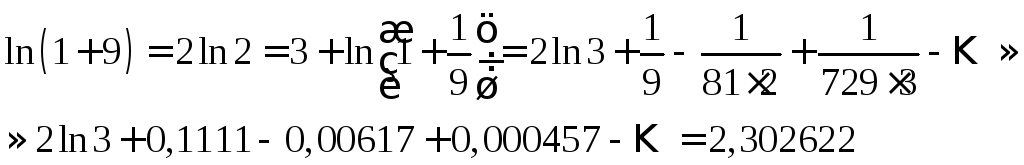
Этот ряд удовлетворяет условиям теоремы Лейбница, поэтому допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов ряда, нетрудно видеть, что следующее за 0,000457 значение.

Получим .

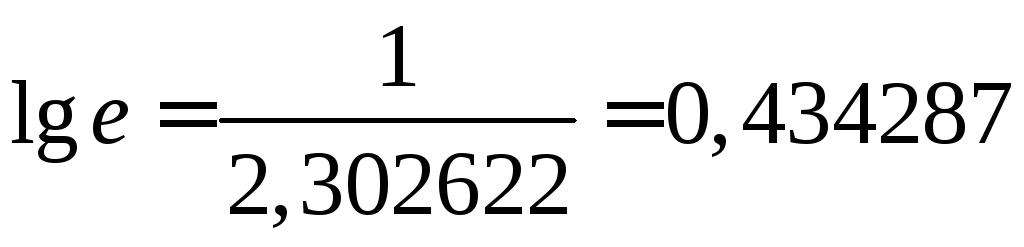Точное значение функции

Ответ: .

Пример 8.Вычислить приближенно с указанной степенью точности .

Решение

Так как ближайшее к 1080 число в десятой степени, то представим

или

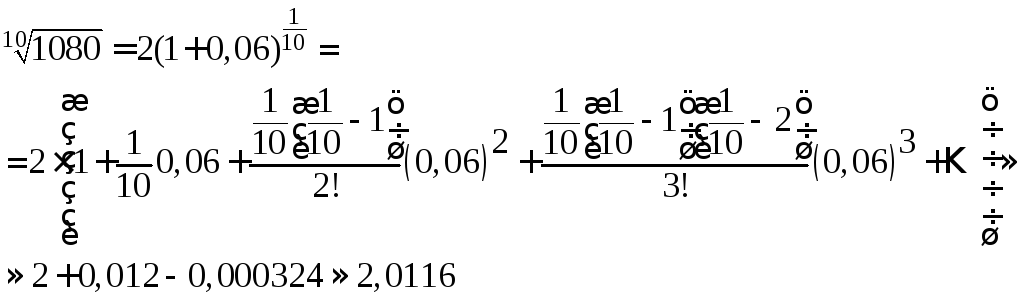
Этот ряд удовлетворяет условиям теоремы Лейбница, поэтому допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов ряда, нетрудно видеть, что .

При получении этого разложения воспользовались разложением в ряд Маклорена для функции:

при

Точное значение выражения .

Пример 9. Вычислить определенный интеграл 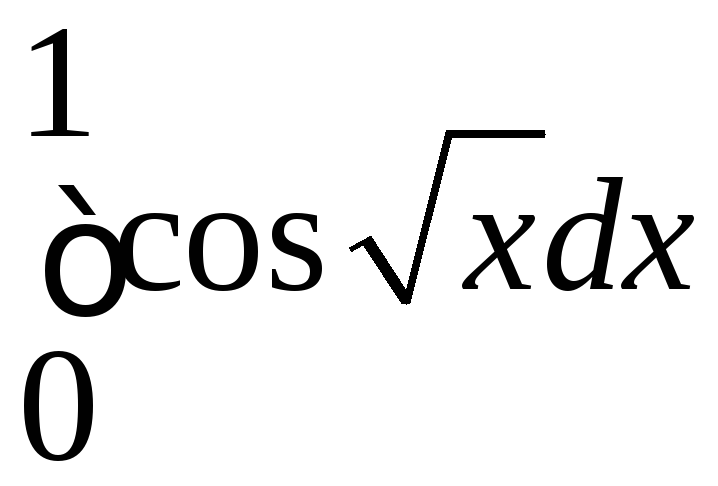с точностью до 0,001, разложив подынтегральную функцию в ряд и затем проинтегрировав его почленно.

Решение

Разложим подынтегральную функцию в ряд Маклорена по следующей формуле:

Тогда, для , получим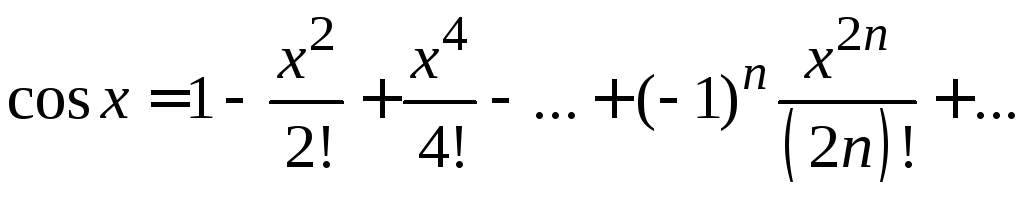

Заменяя в разложении на, имеем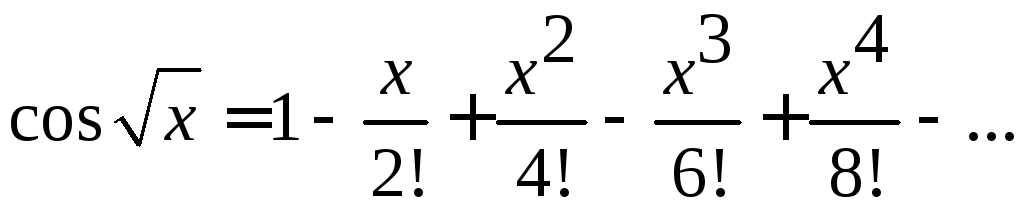и интегрируя в указанных пределах,получим

.

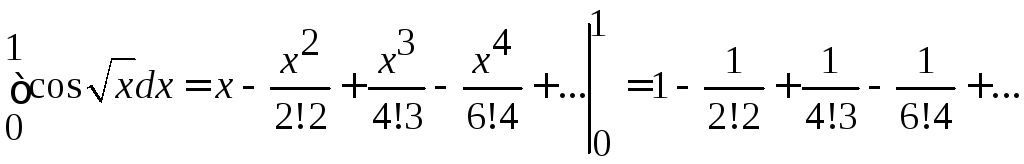Четвертый член этого знакочередующегося сходящегося ряда меньше 0,001. Поэтому для вычисления искомого приближенного значения интеграла достаточно взять три первых члена ряда

.

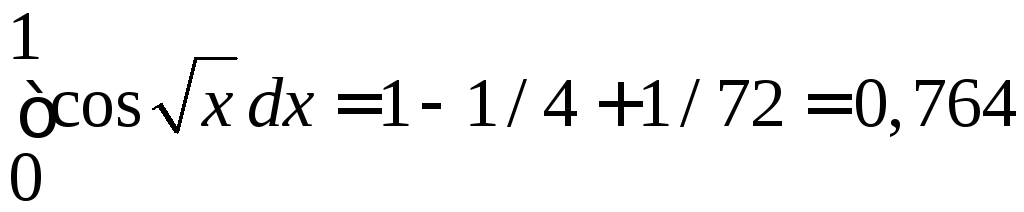Ответ: 0,764.

Приведем разложения некоторых элементарных функций в ряды Маклорена:

1. 

2. 

3. 

4. 

5.