Тема 6. Теория вероятностей Теоретические вопросы

1. Испытания и события.

2. Сформулируйте классическое определение вероятности.

3. Какая группа событий является полной?

4. Для каких задач используются формулы Бейеса? В чем они заключаются?

5. Приведите формулу Бернулли.

6. Сформулируйте локальную и интегральную теорему Муавра-Лапласа.

7. Что называется случайной величиной?

8. Дайте определение непрерывной случайной величины.

9. Какая функция называется функцией плотности распределения вероятностей непрерывной случайной величины, укажите ее свойства.

10. Назовите числовые характеристики случайных величин.

11. Какое распределение называется равномерным?

12. Какое распределение называется нормальным?

13. Сформулируйте центральную предельную теорему.

Методические указания и примеры выполнения заданий

Пример 1. Слово МАТЕМАТИКА составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают без возврата по одной. Найти вероятность, что буквы вынимаются в порядке заданного слова.

Решение. Испытание заключается в вынимании карточек с буквами в случайном порядке без возврата. Элементарным событием является полученная последовательность букв. Событие А состоит в получении нужного слова. Элементарные события являются перестановками из 10 букв, значит . Некоторые буквы в слове математика повторяются, поэтому возможны перестановки, при которых слово не меняется. Их число равно. Таким образом.

Ответ: .

Пример 2. В урне содержится 5 черных и 6 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:

а) 2 белых шара;

б) меньше, чем 2 белых шара;

в) хотя бы один белый шар.

Решение. Испытанием является случайное вынимание четырех шаров. Элементарными событиями являются всевозможные сочетания из 11 шаров по 4. Их число равно

а) А₁ – среди вынутых шаров 2 белых и 2 черных, тогда Следовательно, .

б) А₂ – среди вынутых шаров меньше чем 2 белых. Это событие состоит из двух несовместных событий. В₁ – 1 белый и 3 черных или В2 – среди вынутых шаров нет белых, т.е. . Так как события несовместны, то.

в) А₃ – среди вынутых шаров хотя бы один белый. Найдем вероятность противоположного события: – среди вынутых шаров нет белого., тогда.

Пример 3. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго 0,8, для третьего – 0,9. Найти вероятность того, что в цель попадет хотя бы один стрелок.

Решение. Пусть событие - первый стрелок попал в цель,,; событиеB – второй стрелок попал в цель, ,; событиеС – третий стрелок попал в цель, ,.

Событие D – хотя бы один стрелок попал в цель.

.

Пример 4. По самолету производится три одиночных выстрела. Вероятность попадания при первом выстреле равна 0,4, при втором – 0,5, при третьем – 0,7. Для выхода самолета из строя заведомо достаточно трех попаданий; при одном попадании самолет выходит из строя с вероятностью 0,2, при двух попаданиях - с вероятностью 0,6.

1) Найти вероятность того, что в результате трех выстрелов самолет будет выведен из строя.

2) Известно, что самолет выведен из строя, найти вероятность, что в него попало три снаряда.

Решение. Пусть событие - самолет выведен из строя. Рассмотрим четыре гипотезы:

- в самолет не попало ни одного снаряда,

.

- в самолет попал один снаряд,

.

- в самолет попало два снаряда,

.

- в самолет попало три снаряда,

.

Контрольная формула:

.

- вероятность выхода самолета из строя при осуществлении гипотезы , .

- вероятность выхода самолета из строя при осуществлении гипотезы , .

- вероятность выхода самолета из строя при осуществлении гипотезы , .

- вероятность выхода самолета из строя при осуществлении гипотезы , .

1) Применяя формулу полной вероятности, получим:

.

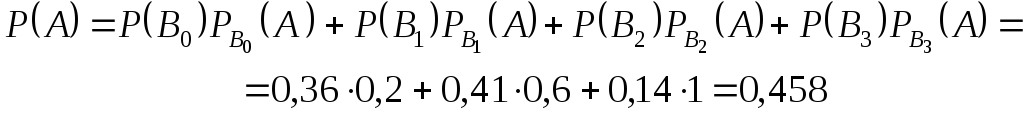2) По формуле Байеса вычислим условные вероятности событий (гипотез).

.

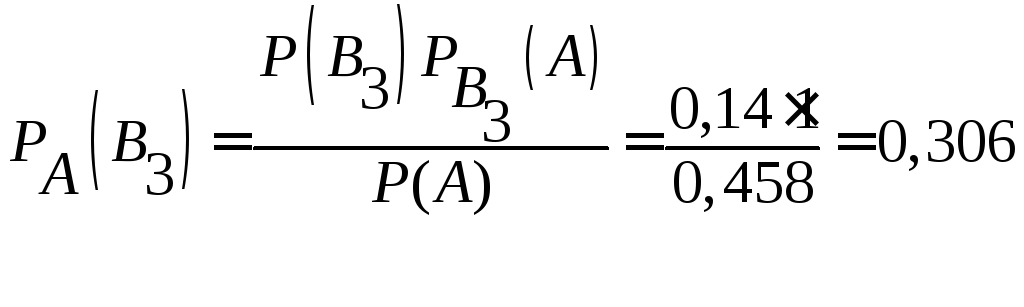Пример 5. В каждом из 6 независимых испытаний событие А происходит с постоянной вероятностью 0,3. Вычислить все вероятности , гдеk – частота события А. Найти наивероятнейшую частоту.

Решение. Используем формулу Бернулли и формулу, с помощью которойвычисляются по значению:

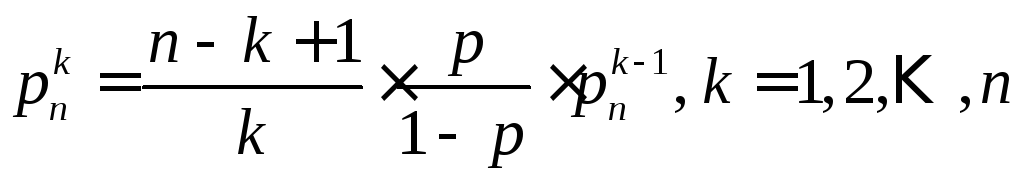. Вычислим значение

Тогда 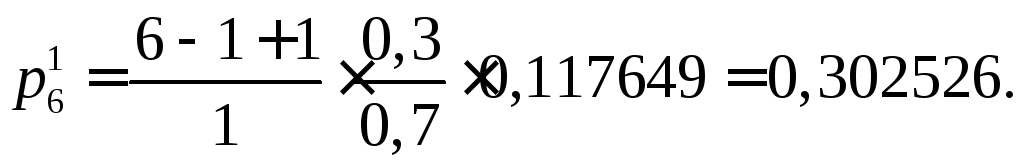Аналогично вычисляем все остальные значения. Результаты занесем в таблицу.

	0,302526
	0,324135
	0,18522
	0,059535
	0,010206
	0,000729
Контроль	1

Найдём наивероятнейшую частоту по заданным условиям:

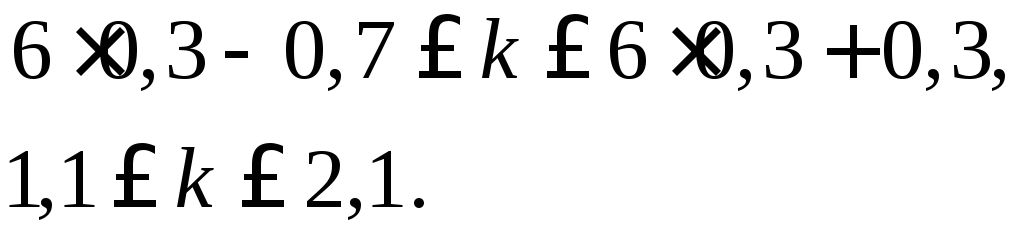
Значит, наивероятнейшая частота и значение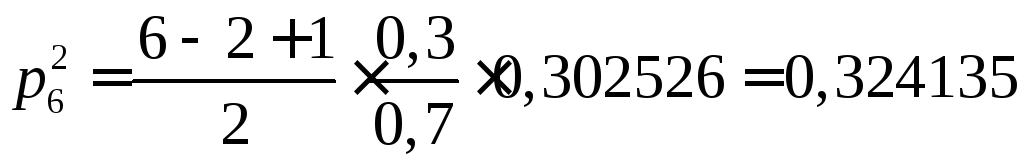является максимальным.

Пример 6. Вероятность поражения цели при одном выстреле равна 0,3. Найти вероятность того, что при 100 выстрелах цель будет поражена 30 раз.

Решение. При решении этой задачи используем локальную теорему Муавра-Лапласа: если при n независимых испытаниях событие А происходит с постоянной вероятностью р, которая не очень близка к нулю и единице, то при достаточно большом числе испытаний n вероятность того, что событие произойдет ровно m раз, приближенно равна

, где .

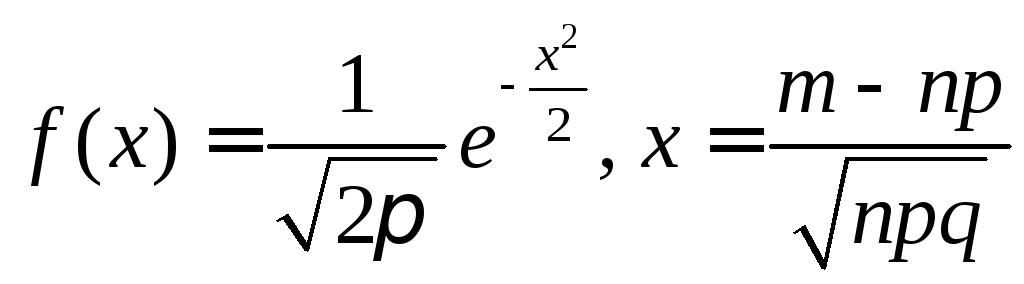Функция чётная и принимает только неотрицательные значения (приложение 3).

Так как ,,,, то получим:

.

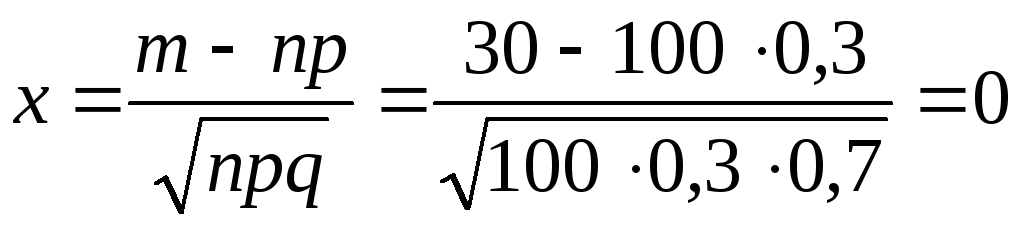Отсюда имеем:

.

Пример 7. Вероятность того, что деталь не прошла проверку ОТК, равна . Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.

Решение. По условию ,,,,. Воспользуемся интегральной теоремой Лапласа:если при n независимых испытаниях событие А происходит с постоянной вероятностью р, которая не очень близка к нулю и единице, то при достаточно большом числе испытаний n вероятность того, что частота m появления события А находится в интервале , приближенно равна

,

где .

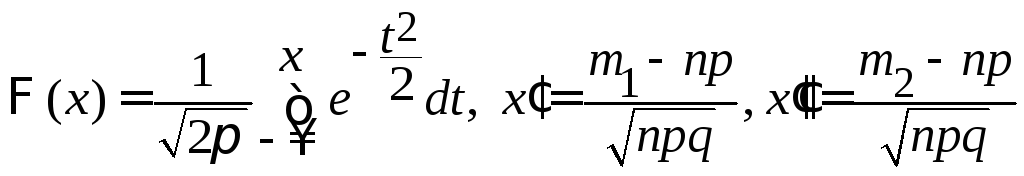Функция Ф(x) принимает значения в интервале , является нечётной. В приложении 4 приведены значения интеграла лишь доx=5, так как для x>5 можно принять Ф(0)=0,5.

По условию ,,,,.

Найдем

,

.

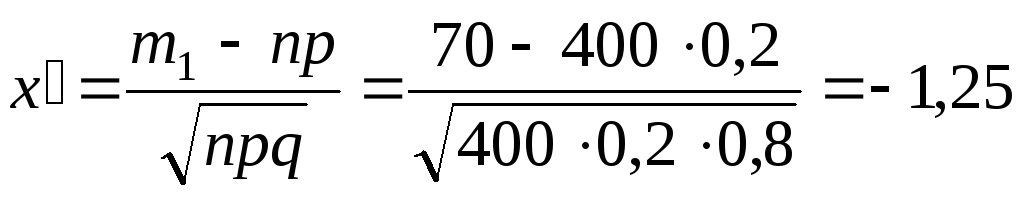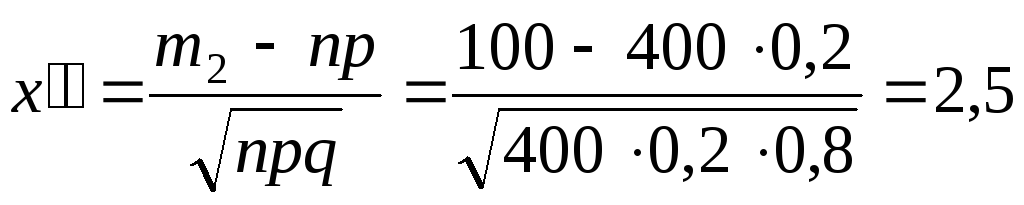Таким образом, получим:

.

Пример 8. Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно равна 0,0001. Найти вероятность того, что тираж содержит 5 бракованных книг.

Решение. По условию ,,. Так как вероятность события мала используем формулу Пуассона. По асимптотической формуле Пуассона искомая вероятность приближенно равна:

.

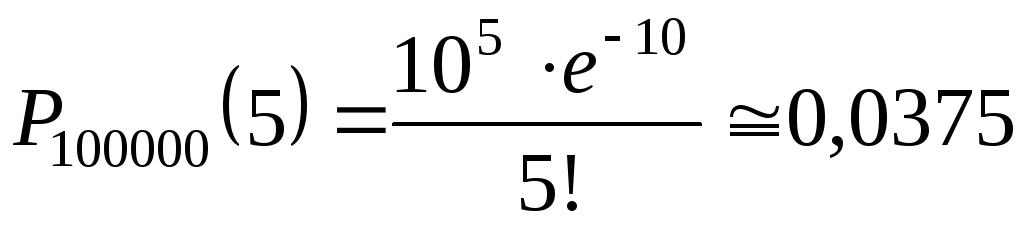Пример 9. Дан ряд распределения случайной величины Х:

	1	3	5	7	9
	0,1	0,4	0,2	0,2	0,1

Найти функцию распределения F(x). Вычислить для X её математическое ожидание, дисперсию и моду.

Решение.

Функцию распределения находим по формуле .

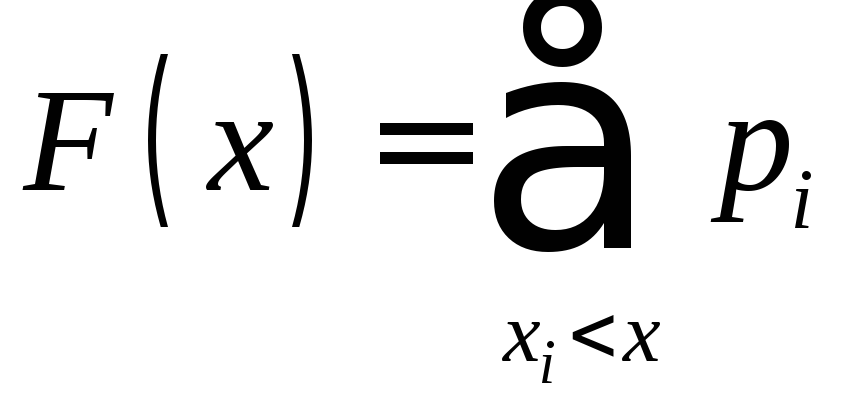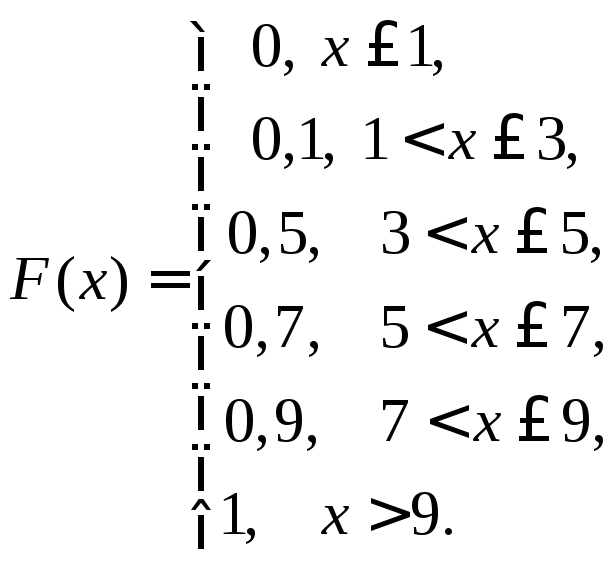
Математическое ожидание вычислим по формуле:

.

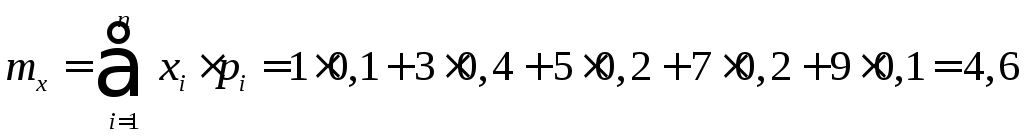Для нахождения дисперсии воспользуемся формулами:

.

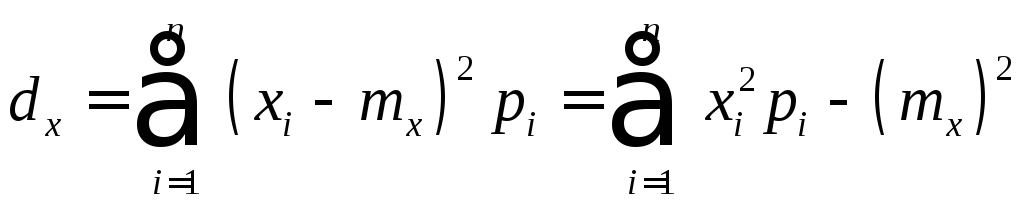
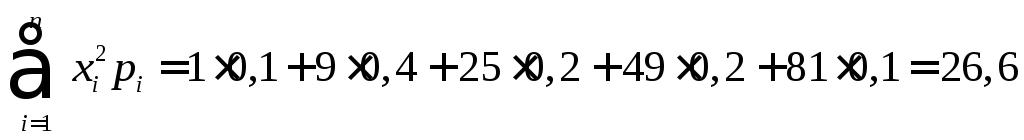Дисперсия случайной величины:

,

откуда легко определить среднеквадратическое отклонение:

.

Моду найдём по максимальной вероятности.

Пример 10. Задана плотность распределения вероятностей непрерывной случайной величины . Требуется:

1). Определить коэффициент ;

2). Найти функцию распределения ;

3). Найти математическое ожидание и дисперсию ;

4).Найти вероятность того, что примет значение из интервала.

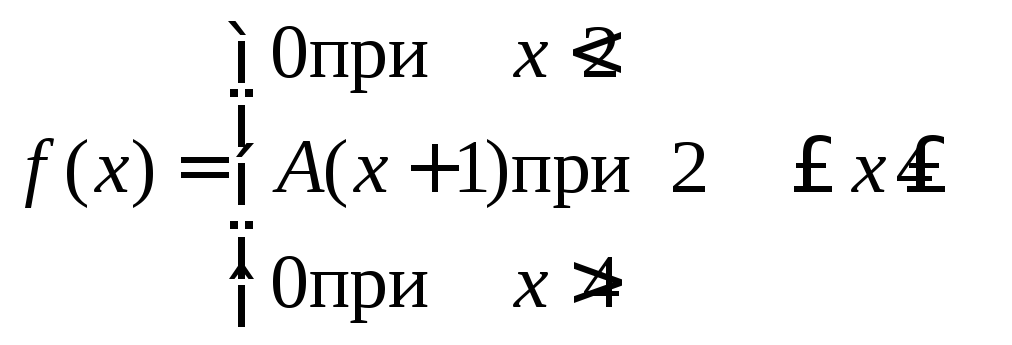
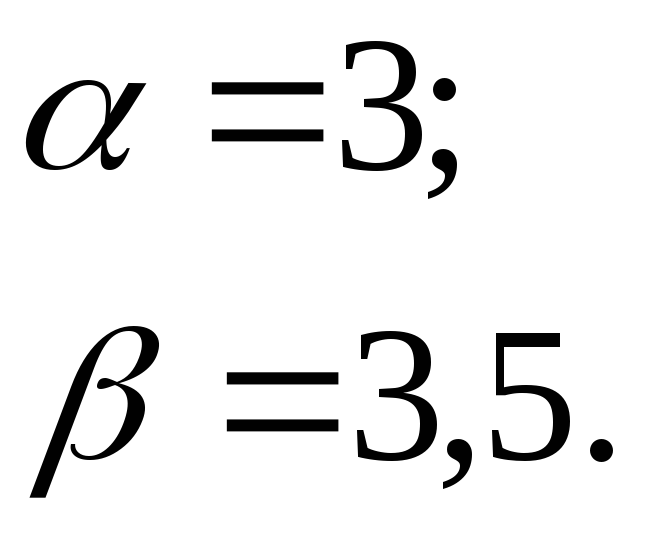
Решение. 1). Для определения коэффициента воспользуемся свойством нормированности плотности распределения: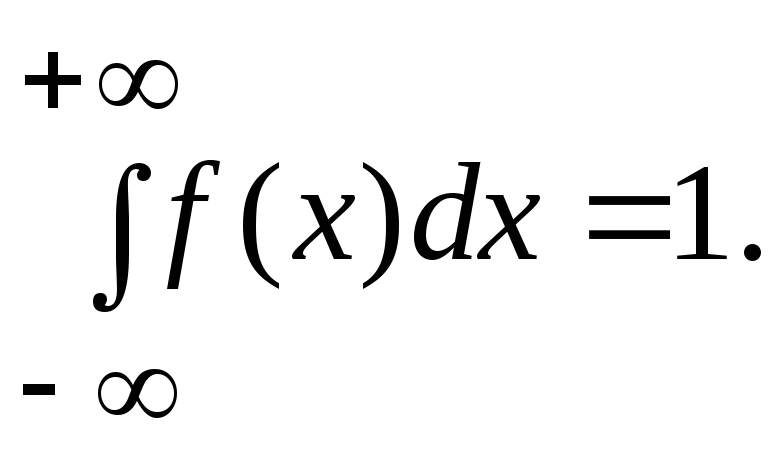

,

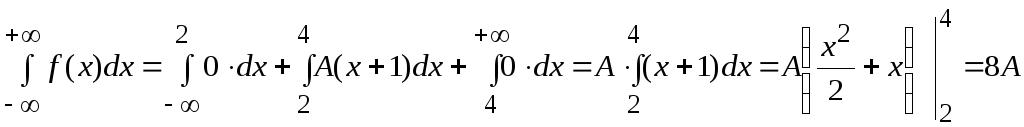т.е. , отсюда. Таким образом,

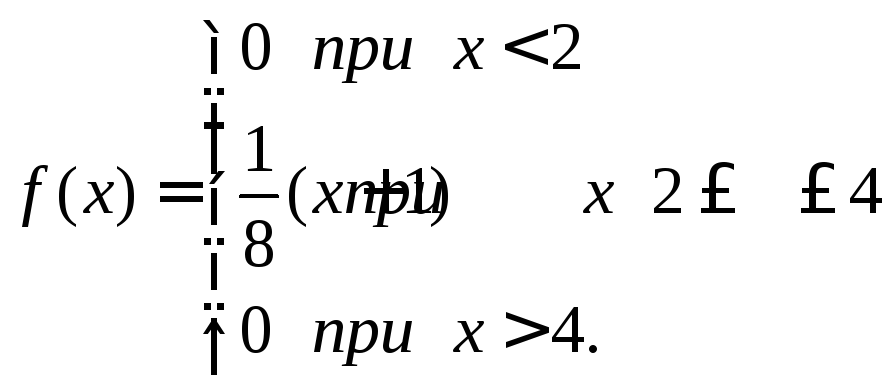
2). Для нахождения функции распределения используем формулу

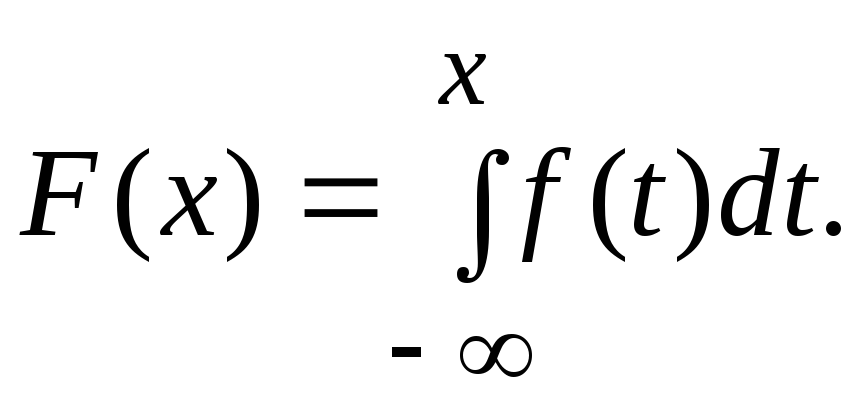
При , имеем: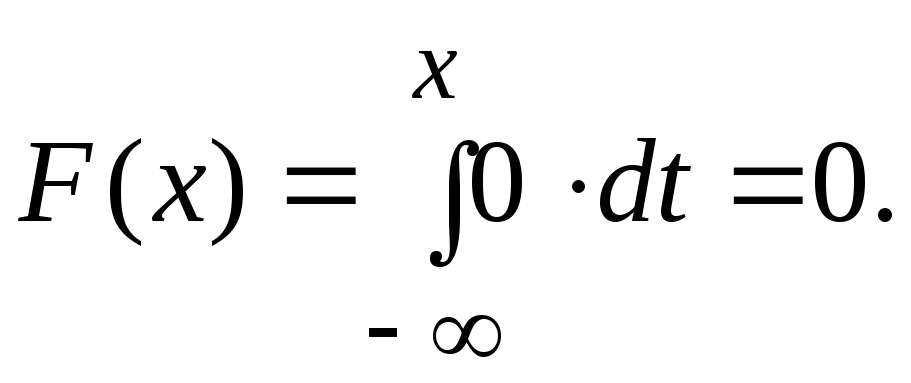

При ,

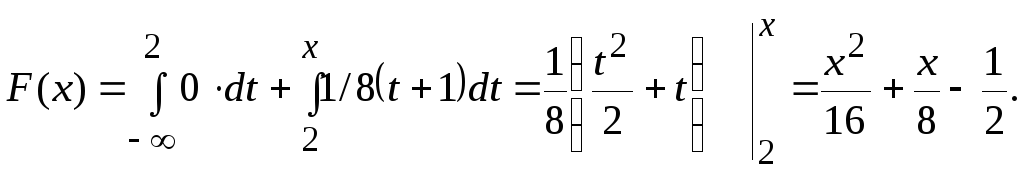
Если ,

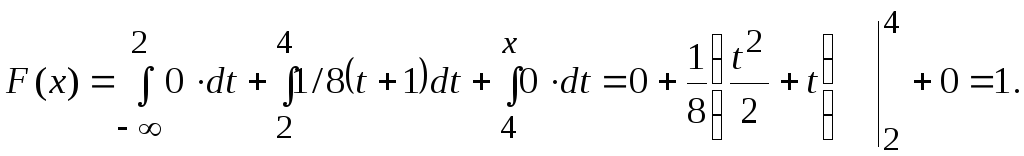
Таким образом,

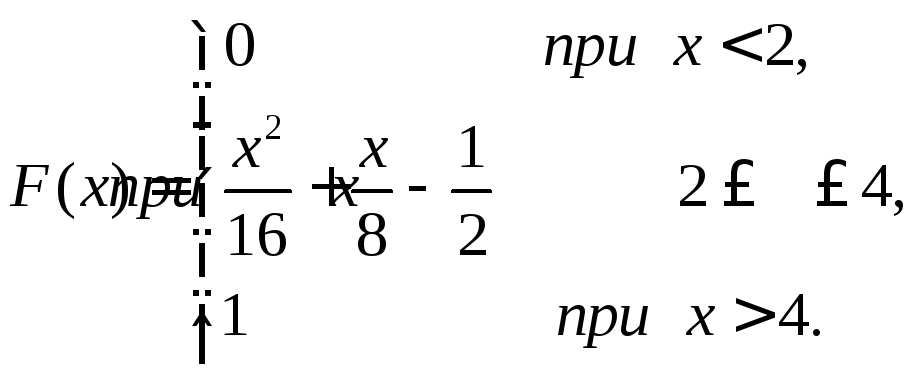
3). Найдем математическое ожидание и дисперсию :

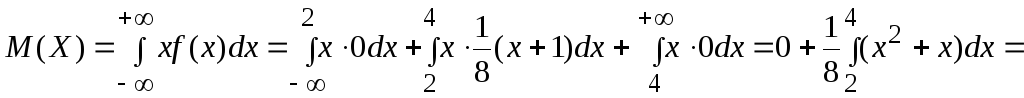
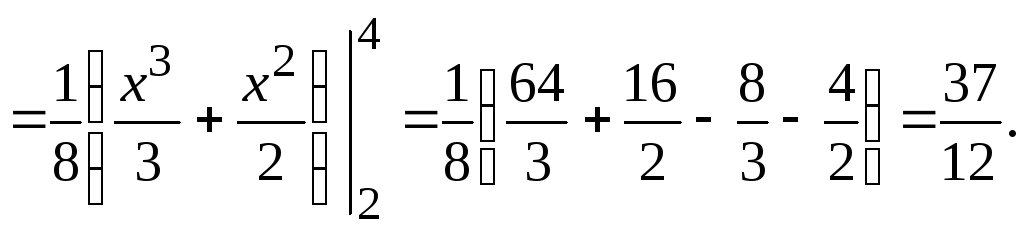
Теперь найдём дисперсию:

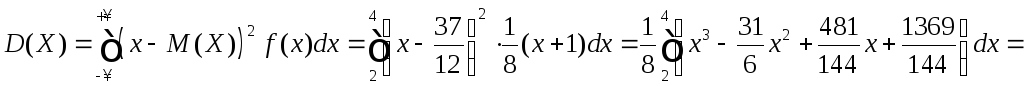
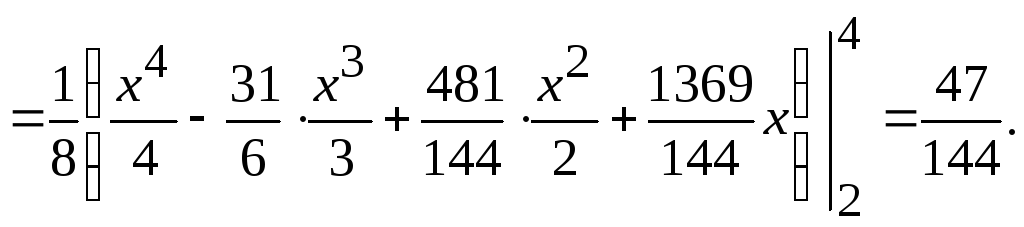
4). Вероятность того, что примет значение из интервала: