Тема 3. Дифференциальные уравнения Теоретические вопросы

1. Задачи, приводящие к дифференциальным уравнениям.

2. Как определяется порядок дифференциального уравнения?

3. Дайте определение общего решения дифференциального уравнения. Сформулируйте задачу Коши.

4. Что называется изоклиной?

5. Уравнения с разделяющимися переменными.

6. Однородные уравнения

7. Метод Бернулли интегрирования линейного дифференциального уравнения первого порядка.

8. Что называется линейным дифференциального уравнения второго порядка?

9. Укажите формулы для решений линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами.

10. Укажите вид частного решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами и правой частью специального вида..

Методические указания и примеры выполнения заданий

Пример 1. Решить уравнение .

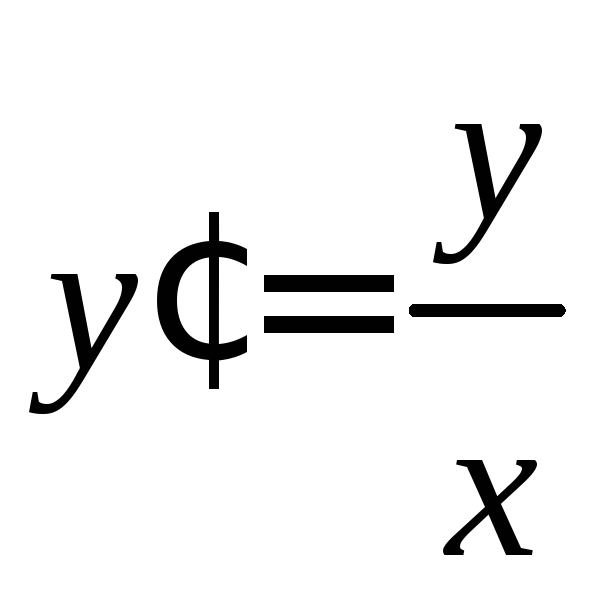Решение.

Данное уравнение относится к классу уравнений с разделяющимися переменными. Разделяя переменные, получаем:

.

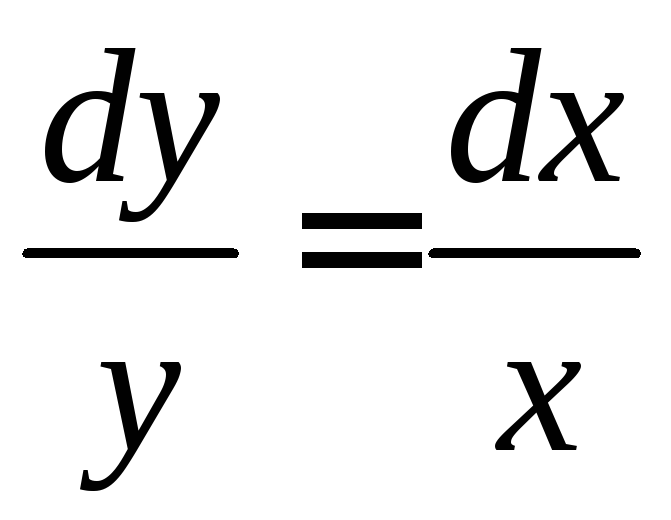Интегрируя, имеем

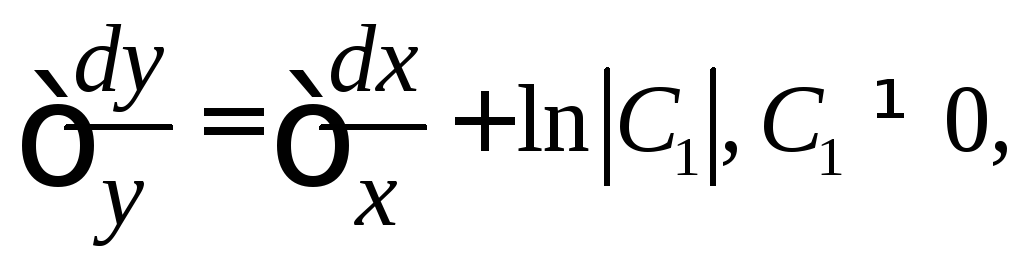или

Тогда: , что эквивалентно уравнению . Полагая, окончательно получаем общее решение данного уравнения

Ответ: .

Пример 2. Решить уравнение .

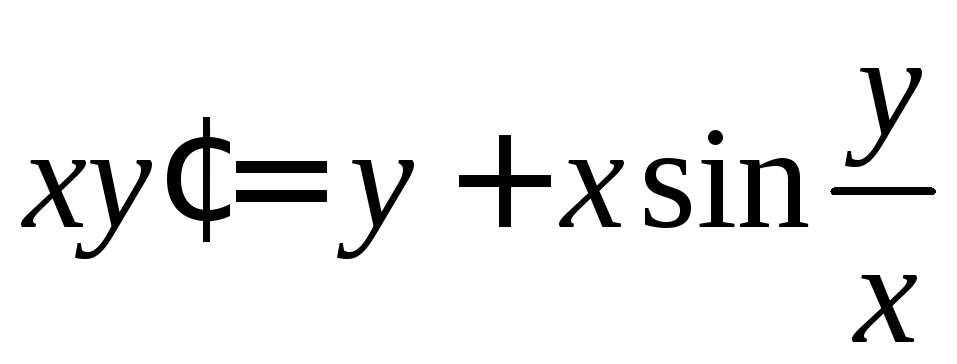Решение. Данное уравнение является однородным дифференциальным уравнением первого порядка. Разделим обе части уравнения на . Получим

.

Сделаем замену и уравнение принимает вид , где - новая неизвестная функция. Осталось решить уравнениеилиДля его решения разделим переменные. Получим. Интегрируя последнее равенство, найдем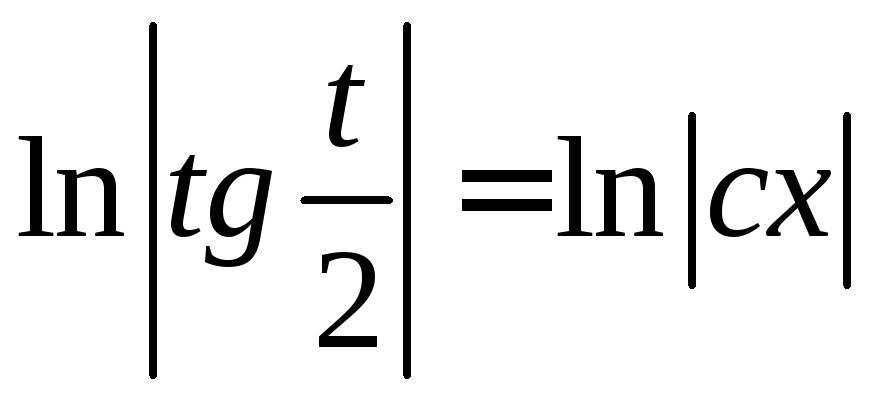(произвольную постоянную можно обозначить). Тогда.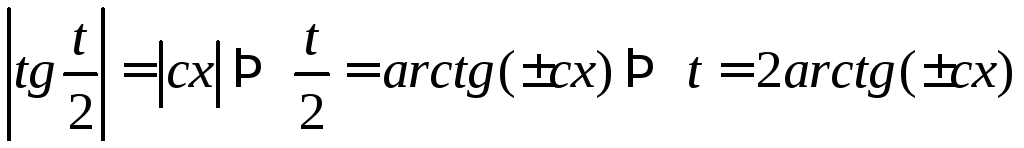

Возвращаясь к исходной неизвестной функции, имеем .

Ответ: .

Пример 3. Решить уравнение

Решение. Разделим уравнение на . Получим линейное уравнение первого порядка. Будем его решать методом Бернулли, т.е. искать решение в виде, гдеподлежат определению. Поскольку, то уравнение принимает вид

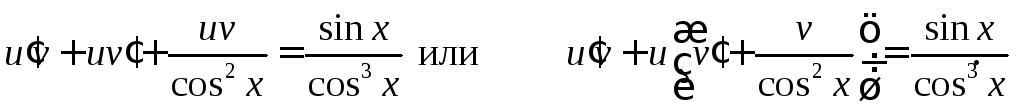
В качестве возьмем любую функцию, такую что , т. е. частное решение уравнения .Это уравнение с разделяющимися переменными, поэтому, умножая его на и деля на, получим

т. е. . Следовательно,(произвольную постоянную полагаем равной нулю).

Подставим найденное v в исходное уравнение, тогда второе слагаемое в правой части обратится в нуль, и для получим уравнение

; .

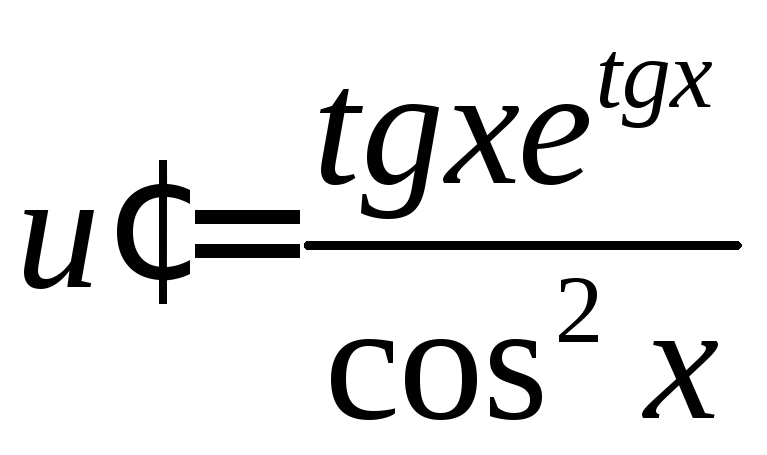Отсюда, используя формулу интегрирования по частям, найдем

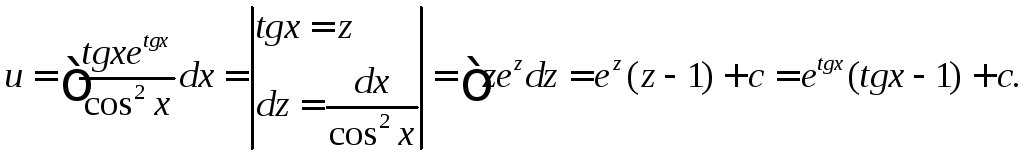
Возвращаясь к исходной неизвестной функции , находим решение:

Ответ:

Пример 4. Найти частное решение уравнения

Решение. Характеристическое уравнение имеет вид ; его корни = 1,=2 действительные и различные. Общее решение уравнения имеет вид . Найдем частное решение. Для этого продифференцируем найденное решение и подставим значения начальных условийи. Решая полученную систему, найдем. Частное решение исходного уравнения, удовлетворяющее заданным начальным условиям, имеет вид.

Ответ: .

Пример 5. Найти частное решение уравнения

.

Решение

Характеристическое уравнение имеет вид ; его корни ==1 действительные и равные. Общее решение уравнения имеет вид . Найдем частное решение. Для этого продифференцируем найденное решение и подставим значения начальных условийи. Частное решение исходного уравнения, удовлетворяющее заданным начальным условиям, имеет вид.

Ответ: .

Пример 6. Найти частное решение уравнения

Решение

Характеристическое уравнение имеет вид ; его корни- комплексные. Соответствующие частные решения уравнения . Общее решение уравнения имеет вид . Найдем частное решение:, тогдаиЧастное решение исходного уравнения, удовлетворяющее заданным начальным условиям, имеет вид.

Ответ: .

Пример 7. Найти общее решение уравнения .

Решение

Характеристическое уравнение имеет корни ,. Значит, общее решение соответствующего однородного уравнения имеет вид. В правой части этого уравнения  произведение многочлена первой степени на показательную функцию при. Так как среди корней характеристического уравнения имеется один корень, совпадающий с параметром, то частное решение данного уравнения ищем в виде

Дифференцируем и подставим в исходное уравнение. Сокращая на , получаем

.

Приравниваем коэффициенты при одинаковых степенях х в обеих частях равенства: , , находим: ,. Подставляя найденные значения A и В в выражение для , получаем частное решение данного уравненияобщее решение имеет вид

Ответ:

Пример 8. Найти общее решение уравнения .

Решение

Характеристическое уравнение имеет корни,. Поэтому общее решение соответствующего однородного уравнения. В правой части равенства  тригонометрическая функция . Правая часть относится к виду. Так как корень характеристического уравнения совпадает с выражением, то частное решение надо искать в виде.

Дифференцируя и подставляя в уравнение, получаем

,

откуда ,. Таким образом, частное решение общее решение уравнения

Ответ: