Индивидуальные задания
Для дифференциальных уравнений без начальных условий найти их общие решения. При наличии начальных условий найти соответствующие этим условиям частные решения.
|
Вариант №1 |
Вариант №2 |
|
1.
2.
3.
4.
5.
6.
|
1.
2.
3.
4.
5.
6.
|
|
Вариант №3 |
Вариант №4 |
|
1.
2.
3.
4.
5.
6.
|
1.
2.
3.
4.
5.
6.
|
|
Вариант №5 |
Вариант №6 |
|
1.
2.
3.
4.
5.
6.
|
1.
2.
3.
4.
5.
6.
|
|
Вариант №7 |
Вариант №8 |
|
1.
2.
3.
4.
5.
6.
|
1.
2.
3.
4.
5.
6.
|
|
Вариант №9 |
Вариант №10 |
|
1.
2.
3.
4.
5.
6.
|
1.
2.
3.
4.
5.
6.
|
|
Вариант №11 |
Вариант №12 |
|
1.
2.
3.
4.
5.
6. |
1.
2.
3.
4.
5.
6.
|
|
Вариант №13 |
Вариант №14 |
|
1.
2.
3.
4.
5.
6. |
1.
2.
3.
4.
5.
6.
|
|
Вариант №15 |
Вариант №16 |
|
1.
2.
3.
4.
5.
6.
|
1.
2.
3.
4.
5.
6.
|
|
Вариант №17 |
Вариант №18 |
|
1.
2.
3.
4.
5.
6.
|
1.
2.
3.
4.
5.
6.
|
|
Вариант №19 |
Вариант №20 |
|
1.
2.
3.
4.
5.
6.
|
1.
2.
3.
4.
5.
6.
|
|
Вариант №21 |
Вариант №22 |
|
1.
2.
3.
4.
5. 6.
|
1.
2.
3.
4.
5.
6.
|
|
Вариант №23 |
Вариант №24 |
|
1.
2.
3.
4.
5. 6.
|
1.
2.
3.
4.
5.
6.
|
|
Вариант №25 |
Вариант №26 |
|
1.
2.
3.
4.
5.
6.
|
1.
2.
3.
4.
5.
6.
|
|
Вариант №27 |
Вариант №28 |
|
1.
2.
3.
4.
5.
6.
|
1.
2.
3.
4.
5.
6.
|
|
Вариант №29 |
Вариант №30 |
|
1.
2.
3.
4.
5. 6. |
1.
2.
3.
4.
5. 6.
|
;
;
;
;
;
;
, 
;
;
;
;
, 
;
;
;
;
;
, 
;
;
;
;
;
, 
;
;
;
, 
;
;
;
, 
;
;
;
,
;
;
;
, 
;
;
;
, 
;
;
;
, 
;
;
;
;
, 
;
;
;
, 
;
;
;
;
, 
;
;
, 
;
;
;
, 
;
;
;
, 
;
;
;
, 
;
;
, 
;
;
;
;
, 
;
;
;
;
, 
;
;
;
;
, 
;
;
;
;
, 
;
;
;
, 
;
;
;
;
, 
;
;
;
, 
;
;
;
;
, 
;
;
;
;
,
;
;
;
;
, 
;
;
;
, 
;
;
Тема 4. Ряды Теоретические вопросы
1. Что называется числовым рядом? Какие ряды называются сходящимися?
2.
Можно ли утверждать, что ряд
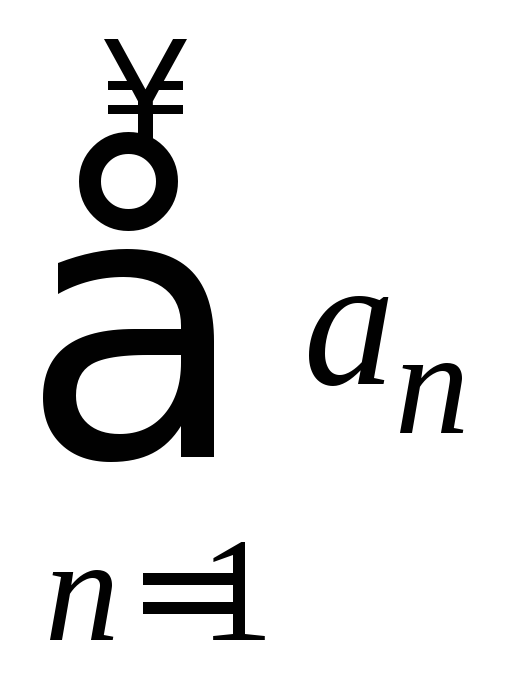сходится, если
.
3. Верно ли, что если ряд сходится, то его частичные суммы ограничены.
4. Существует ли ряд, который по признаку Даламбера сходится, а по признаку Коши расходится.
6. Сформулируйте интегральный признак сходимости.
7. Верно ли, что если ряд сходится абсолютно, то он сходится и условно?
8. Сформулируйте теорему Лейбница.
9. Существует ли степенной ряд, для которого верно следующее утверждение: на обоих концах интервала ряд расходится?
10.
Может ли интервал сходимости ряда
быть таким: (-2;0).