2.2. Производная функции. Приложения производных Теоретические вопросы

1. Определение производной. Уравнение касательной и нормали к кривой.

2. Производная суммы, разности, произведения и частного.

3. Производная сложной функции.

4. Производные основных элементарных функций.

5. Логарифмическое дифференцирование.

6. Дифференциал функции.

7. Правила Лопиталя.

8. Возрастание и убывание функций. Максимум и минимум.

9. Выпуклость графика функции. Точки перегиба.

10. Асимптоты графика функции.

11. Общая схема исследования функции и построение ее графика.

12. Функции двух переменных.

13. Частные производные первого порядка, их геометрический смысл. Градиент.

14. Экстремум функции двух переменных.

Методические указания и примеры выполнения заданий

Пример 1

Найти производные следующих функций:

1. ; 2.; 3.; 4.

Решение:

1. Используем правило дифференцирования произведения и таблицу производных:.

2. Используем правило дифференцирования частногои таблицу производных:.

3. Обозначим , тогда. По правилу дифференцирования сложной функции имеем

.

4. Найдем производную сложной функции .

Пример 2

Применяя предварительное логарифмирование, вычислить производную функции .

Решение:

Прологарифмируем левую и правую часть выражения

Дифференцируя левую и правую часть, получаем

,

.

Ответ: .

Пример 3

Применяя правило Лопиталя, найти предел функции .

Решение:

Подстановка предельного значения аргумента приводит к неопределенности вида, т.к.и. Производные функцийисуществуют, причем. Наконец, существует предел отношения производных. Поэтому применимо правило Лопиталя:

Ответ: 3.

Пример 4

Методами дифференциального исчисления исследовать функции и построить их графики по следующей схеме:

1. –область определения функции;

2. Чётность, нечётность функции;

3. Периодичность;

4. Точки пересечения с осями;

5. Экстремум функции, промежутки возрастания, убывания функции;

6. Выпуклость, вогнутость функции. Точки перегиба;

7. Асимптоты;

8. Пределы функции на если нет асимптот;

9. Построение графика функции.

10. -множество значений функции.

а) Исследовать функцию и построить ее график

Решение.

1. . Функция непрерывна, особых точек нет.

2. Функция общего типа.

3. Функция непериодична.

4. Точки пересечения с осями:

,

–корень, т. к. .

Следовательно, после деления на множитель x+2 получаем

Итак, имеем три точки пересечения с осью OX: (-2,0), (-0.3,0), (-3.7,0),

. Точка пересечения с осью ординат - (0,2).

5. Точки экстремума, промежутки возрастания и убывания функции.

;

Результаты исследований занесём в таблицу:

x	(-¥,-3)	-3	(-3,-1)	-1	(-1,¥)
f¢(x)	+	0	-	0	+
f(x)		2		-2
		max		min

6. Выпуклость, вогнутость функции, точки перегиба.

Результаты исследования занесем в таблицу:

x	(-¥,-2)	-2	(-2,¥)
f¢¢(x)	-	0	+
f(x)	Ç	0	È
		т.п.

7. Асимптот нет.

8. Рассмотрим пределы функции на +¥, -¥.

9. Построение графика функции.

9. 

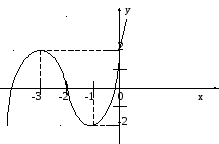
б) Исследовать функцию и построить график

Решение.

1. . Функция не определена в точках.

2. Чётность, нечётность. Функция нечётная, т.к. y(-x)=-y(x)

3. Функция непериодическая.

4. Точки пересечения с осями:

Точка пересечения с осью OX - (0,0).

.

Точка пересечения с осью OY - (0,0 ).

5. Точки экстремума, промежутки возрастания и убывания функции.

что невозможно, следовательно, функция точек экстремума не имеет. Так как - функция убывает на всей своей области определения.

6. Выпуклость, вогнутость функции, точки перегиба.

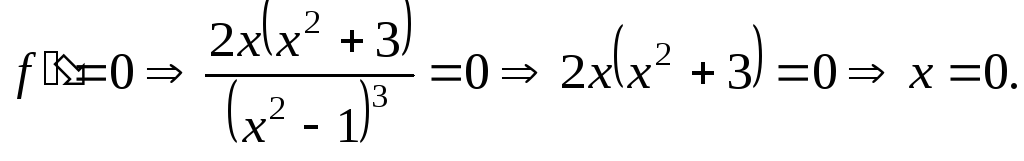
Результаты исследования занесем в таблицу:

x	(-¥,-1)	-1	(-1,0)	0	(0,1)	1	(1,¥)
f¢¢(x)	-	не сущ.	+	0	-	не сущ.	-
f(x)	Ç	не сущ.	È		Ç	не сущ.	È
				т.п.

Особо были исследованы на выпуклость и вогнутость окрестности точек, в которых не существует.

7. Асимптоты.

–вертикальные асимптоты.

–наклонная асимптота, где

y=0 – горизонтальная асимптота, как частный случай наклонной.

Найдем пределы функции слева и справа от вертикальных асимптот.

8. Рассмотрим пределы функции на

9. Построение графика функции.

9. .

Пример 5.

Найти частные производные первого и второгопорядков функции .

Решение.

Вычислим частные производные первого порядка, рассматривая в первом случае y как постоянную величину, а во втором – x, и, пользуясь правилами дифференцирования сложной функции:

;

.

Аналогично вычислим частные производные второго порядка:

;

;

.