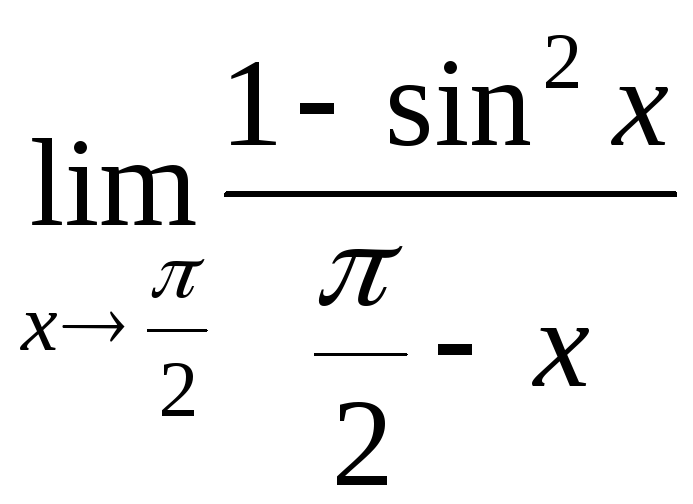- •Тема 1. Элементы линейной алгебры. Теоретические вопросы
- •Методические указания и примеры выполнения заданий
- •Индивидуальные задания
- •Тема 2. Основы математического анализа
- •2.1. Функции. Предел и непрерывность функции. Теоретические вопросы
- •Методические указания и примеры выполнения заданий
- •Индивидуальные задания
- •2.2. Производная функции. Приложения производных Теоретические вопросы
- •Методические указания и примеры выполнения заданий
- •Индивидуальные задания
- •Методические указания и примеры выполнения заданий
- •Индивидуальные задания
- •Тема 3. Дифференциальные уравнения Теоретические вопросы
- •Методические указания и примеры выполнения заданий
- •Индивидуальные задания
- •Тема 4. Ряды Теоретические вопросы
- •Методические указания и примеры выполнения заданий
- •Индивидуальные задания
- •Тема 5. Исследование операций Теоретические вопросы
- •Методические указания и примеры выполнения заданий
- •Индивидуальные задания
- •1. Ресурсная задача.
- •2. Транспортная задача.
- •Тема 6. Теория вероятностей Теоретические вопросы
- •Методические указания и примеры выполнения заданий
- •Индивидуальные задания
- •Тема 7. Математическая статистика Теоретические вопросы
- •Методические указания и примеры выполнения заданий
- •Индивидуальные задания
- •Приложения
- •Критические точки распределения Стьюдента
- •Критические точки распределения
- •Литература
- •Оглавление
Методические указания и примеры выполнения заданий
Пример 1
Найти
область определения функции
![]() .
.
Решение:
Первое слагаемое принимает действительные
значения при
![]() ,
а второе при
,
а второе при![]() .
Решим указанную систему неравенств:
.
Решим указанную систему неравенств: .
.
Следовательно,
область определения отрезок
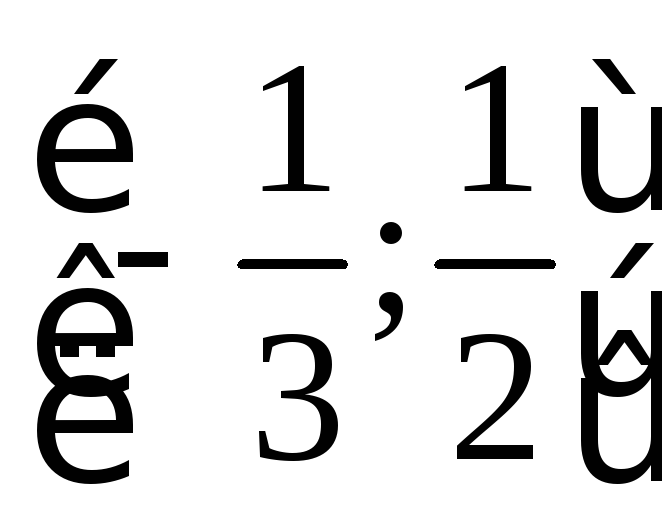
Ответ:
 .
.
Пример 2
Вычислить
предел
![]()
Решение:
Имеем неопределенность вида
![]() .
В подобных примерах, когда в числителе
и знаменателе многочлены, их необходимо
разложить на множители, после этого
дробь сократить и затем перейти к пределу
.
В подобных примерах, когда в числителе
и знаменателе многочлены, их необходимо
разложить на множители, после этого
дробь сократить и затем перейти к пределу
![]() .
.
Ответ:
![]() .
.
Пример 3
Вычислить
предел
![]() .
.
Решение:
Непосредственная подстановка предельного
значения аргумента приводит к
неопределенности вида
![]() .
Если под знаком предела имеется
иррациональность, то для раскрытия
неопределенности вида
.
Если под знаком предела имеется
иррациональность, то для раскрытия
неопределенности вида![]() необходимо перенести иррациональность
из числителя в знаменатель или из
знаменателя в числитель, а иногда и то
и другое, полученную дробь сократить и
воспользоваться теоремами о пределах.
Умножим числитель и знаменатель на
выражение сопряженное к числителю и на
выражение сопряженное к знаменателю и
применим формулу разности квадратов.
необходимо перенести иррациональность
из числителя в знаменатель или из
знаменателя в числитель, а иногда и то
и другое, полученную дробь сократить и
воспользоваться теоремами о пределах.
Умножим числитель и знаменатель на
выражение сопряженное к числителю и на
выражение сопряженное к знаменателю и
применим формулу разности квадратов.
![]()
![]()
Ответ:
![]() .
.
Пример 4
Вычислить
предел

Решение:
В
данном примере имеем неопределенность
вида
![]() .
В подобных примерах, для раскрытия
неопределенности числитель и знаменатель
необходимо делить на степеньх
с наивысшим показателем, а затем перейти
к пределу, применяя теоремы о пределах
.
В подобных примерах, для раскрытия
неопределенности числитель и знаменатель
необходимо делить на степеньх
с наивысшим показателем, а затем перейти
к пределу, применяя теоремы о пределах

 .
.
Ответ:
![]() .
.
Пример 5
Вычислить
предел ![]()
Решение:
Преобразуем разность синусов и используем
формулу
![]() (первый замечательный предел) и свойства
пределов.
(первый замечательный предел) и свойства
пределов.

Ответ:
![]() .
.
Пример 6
Вычислить
предел
![]()
Решение:
В
этом примере предел основания равен 1
(следует разделить числитель на
знаменатель), а показатель степени
стремится к бесконечности. Имеем
неопределенность вида
![]() .
Используем второй замечательный предел-
.
Используем второй замечательный предел- .
Сделав очевидные преобразования, получим
.
Сделав очевидные преобразования, получим

Ответ:
![]() .
.
Весьма полезными при нахождении пределов функций является знание следующих пределов
![]() (1)
(1)
![]() (2)
(2)
![]() (a>0)
(3)
(a>0)
(3)
![]() (4)
(4)
Пример 7
Вычислить
предел
![]() .
.
Решение:
Заменяя разность логарифмов логарифмом дроби, и, используя формулу (1), получим

Ответ:3.
Индивидуальные задания
а). Найти область определения функции.
б). Вычислить следующие пределы, не пользуясь правилом Лопиталя
|
1.
а).
|
б)
|
| |
|
2.
а).
|
б)
|
| |
|
3.
а).
|
б)
|
| |
|
4.
а).
|
б)
|
| |
|
5.
а).
|
б)
|
| |
|
6.
а).
|
б)
|
| |
|
7.
а).
|
б)
|
| |
|
8.
а).
|
б)
|
| |
|
9.
а).
|
б)
|
| |
|
10.
а).
|
б)
|
| |
|
11.
а).
|
б)
|
| |
|
12.
а).
|
б)
|
| |
|
13.
а).
|
б)
|
| |
|
14.
а).
|
б)
|
| |
|
15.
а).
|
б)
|
| |
|
16.
а).
|
б)
|
| |
|
17.
а).
|
б)
|
| |
|
18.
а).
|
б)
|
| |
|
19.
а).
|
б)
|
| |
|
20.
а).
|
б)
|
| |
|
21.
а).
|
б)
|
| |
|
22.а). |
б)
|
| |
|
23.
а).
|
б)
|
| |
|
24.
а).
|
б)
|
| |
|
25.
а).
|
б)
|
| |
|
26.
а).
|
б)
|
| |
|
27.
а).
|
б)
|
| |
|
28.а).
|
б)
|
| |
|
29.
а).
|
б)
|
| |
|
30.
а).
|
б)
|
| |






 ;
;