Глава 2.

ОСНОВЫ ТЕОРИИ ПОГРЕШНОСТЕЙ И ОБРАБОТКИ

РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ

Погрешности измерений классифицируют ,по ряду признаков: форме выражения, причинам возникновения, характеру прояв­ления и др.

Классификация погрешностей по форме выражения. По фор­ме выражения погрешности подразделяют на абсолютные и отно­сительные. Погрешность, выраженная в единицах измеряемой ве­личины, называется абсолютной. Например, AU= 1 мВ, AF=l Гц и т. д. Если измеренная величина превышает действительное зна­чение, погрешность положительна, если же действительное значе­ние больше измеренного — отрицательна. Абсолютная погреш­ность характеризует качество измерений только однородных ве­личин примерно одинакового размера. Относительной погреш­ностью называется отношение абсолютной погрешности к истин­ному значению измеряемой величины: 6Q=AQ/Q_Hc»»AQ/Q_a.

Относительная погрешность ¹может характеризовать качест­во измерений как разнородных величин, так и однородных вели­чин разного размера.

Для оценки качества измерения необходимо вычислить относи­тельные погрешности: меньшая погрешность при прочих равных условиях характеризует более высокое качество измерений.

В метрологии пользуются понятием точность измерений. Точ­ность — величина, обратная относительной погрешности. Если, например, относительная погрешность равна 0,01, то точность составит 100. Как правило, относительные погрешности выража­ют в процентах.

Классификация погрешностей по причине возникновения. Каж­дый из элементов процесса измерения может быть причиной, ис­точником погрешности. По причинам возникновения погрешности разделяют на две группы: объективные погрешности, не связан­ные с человеком-оператором, производящим измерения, и субъ­ективные (личные), обусловленные экспериментатором, состояни­ем его органов чувств, опытом и т. д. При использовании циф­ровых измерительных приборов субъективные погрешности отсут­ствуют. В свою очередь, объективные погрешности разделяются на погрешности опознания объекта, методические, инструменталь­ные погрешности и погрешности, обусловленные внешними усло­виями.

Погрешности опознания объекта измерения связаны с несоот­ветствием реального объекта принятой модели. Пусть, например, объектом измерения является переменный ток, а принятая мо­дель — синусоидальная форма тока. Если нас интересует ампли­туда тока, то мы вправе выбрать любой метод и средство изме­рения, позволяющие измерить амплитуду тока синусоидальной формы. Это может быть прибор, измеряющий средневыпрям- ленное или среднеквадратическое значение. Реальный же объект может иметь несинусоидальную форму. Наличие гармонических составляющих тока в зависимости от используемого метода и средств измерения вызовет ту или иную погрешность. Для исклю­чения этой погрешности требуется переопределение модели, кото­рое производится путем замены гармонического колебания сум­мой гармонических колебаний, а также уточнением самой задачи: интересует нас амплитуда несинусоидального колебания или амп­литуда его первой гармоники.

Погрешности метода обусловлены несовершенством метода из­мерений, упрощающими предположениями, принятыми при обос­новании метода. К этим погрешностям относятся составляющие погрешности, вызываемые влиянием средства измерения на изме­ряемую цепь. Например, погрешность, обусловленная шунтирую­щим действием сопротивления вольтметра при измерении паде­ния напряжения на резисторе, имеющем большое сопротивление. Часто к методическим относят и погрешность опознания объекта.

Инструментальные погрешности —■ погрешности из-за несовер­шенства средств измерения, их схемы, конструкции, состояния в процессе эксплуатации. Каждое средство измерения характеризу­ется свойственной ему погрешностью, которая входит в общую погрешность измерения.

Классификация погрешностей измерений по закономерностям проявления. По закономерностям проявления различают система­тические, случайные, грубые погрешности измерений и промахи.

Систематическая погрешность Д_с — это составляющая погреш­ности измерения, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины в одних и тех же условиях. Закономерно изменяющаяся система­тическая погрешность, в свою очередь, может быть прогрессирую­щей (возрастающей, убывающей), периодической или изменяю­щейся по сложному непериодическому закону.

К постоянным систематическим погрешностям относят погреш­ность градуировки шкалы, погрешность значения меры, темпера­турную погрешность и т. д.

К переменным систематическим погрешностям относят погреш­ности, обусловленные изменением напряжения питания (разряд аккумуляторной батареи), погрешности, связанные с действием электромагнитных помех, влиянием отражений и т. д. Системати­ческие погрешности могут быть обнаружены й оценены.

Анализ источников возникновения систематических погрешнос­тей — одна из основных задач при проведении точных измере­ний. Ее решение требует глубокого понимания принципа работы средств измерений, особенностей схемы и конструкции. Однако разработаны и общие способы учета и исключения систематичес­ких погрешностей, на которых мы остановимся в § 2.3. Если сис­тематическая погрешность достаточно точно определена, она мо­жет быть исключена введением поправки или поправочного мно­жителя.

Поправка — значение величины, одноименной с измеряемой, прибавляемое к измеренной величине для исключения системати­ческой погрешности. Поправка равна абсолютной систематической погрешности с обратным знаком.

Поправочный множитель — число,- на которое умножают ре­зультат измерения с целью исключения систематической погреш­ности.

Полностью исключить систематические погрешности нельзя, всегда имеется неисключенный остаток систематической погреш­ности (НСП).

Случайная погрешность А •— составляющая погрешности из­мерения, которая при повторных измерениях в одних и тех же ус­ловиях изменяется случайным образом, без внднмой закономер­ности. Случайные погрешности являются следствием случайных процессов, протекающих в измерительных цепях. Вообще говоря, в природе, как известно, имеют место детерминированные про­цессы с причинно-следственными связями между величинами и параметрами, нх характеризующими. Однако когда интенсивность какого-то процесса мала, а на него накладывается множество других, установить закономерности сложного процесса не пред­ставляется возможным. Иногда этот сложный процесс рассматри­вают как случайный, а результаты отдельных измерений как слу­чайные величины. Для оценки погрешностей и разработки спосо­бов уменьшения их влияния на результат измерения используют аппарат теории вероятностей и математической статистики. Оче­видно, по мере того, как будут изучены отдельные процессы из множества, установлены их закономерности, погрешности нз слу­чайных перейдут в категорию систематических.

Таким образом, результат измерения всегда содержит как сис-

тематическую, так и случайную погрешность: Д=Д₀+Д. Поэтому погрешность результата измерения в общем случае нужно рас­сматривать как случайную величину. Тогда систематическая пог­решность является математическим ожиданием этой величины A_c=Af[A], а случайная погрешность — центрированной случай­ной величиной.

Говоря о свойствах погрешностей, различают также грубые погрешности и промахи.

Грубой погрешностью называют погрешность, существенно превышающую погрешность, оправданную условиями измерения, свойствами примененных средств измерений, методом измерения, квалификацией экспериментатора. Грубые погрешности могут появляться вследствие резкого и кратковременного изменения влияющей на результат измерения величины. Грубые погрешности обнаруживают статистическими методами и исключают из рас­смотрения.

Промахи являются следствием неправильных действий экспери­ментатора. Это может быть описка при записи результатов, не­правильно снятые показания прибора и т. д. Промахи обнаружи­вают нестатистическими методами, их следует всегда исключать из рассмотрения.

Завершая классификацию погрешностей, необходимо отметить, что погрешности разделяют также на статические и динамические. Статические погрешности имеют место при статических измерени­ях, т. е. при неизменной во времени измеряемой величине, дина­мические — при динамических измерениях, т. е. при переменной во времени измеряемой величине. Целью динамического измере­ния и является измерение этой функции времени. Динамическая погрешность возникает вследствие инерционных свойств средств измерений. Для оценки динамической погрешности необходимо знать передаточную функцию средства измерения, а также харак­тер изменения измеряемой величины. Метрология динамических измерений находится в стадии становления.

2. ОЦЕНИВАНИЕ И СПОСОБЫ УМЕНЬШЕНИЯ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ

Математическое описание случайных погрешностей. Выше от­мечалось, что измеряемая величина, содержащая случайную пог­решность, должна рассматриваться как случайная величина. На­помним, что наиболее общей характеристикой непрерывной слу­чайной величины X является плотность распределения ее вероят­ностей.

Плотность распределения вероятностей dx

где dF(x) — вероятность значений случайной величины х в ин­тервале dx.

Наряду с плотностью распределения вероятностей использует­ся функция распределения вероятностей случайной величины

*(f(x)dx,

•—OQ

которая выражает собой вероятность того, что случайная величи­на находится в интервале от —оо до некоторого значения, мень­шего Xi ¹.

Функция распределения любой случайной величины является неубывающей функцией, определенной так, что F(—оо) =0, а F( + oo) = 1. Вероятность того, что случайная величина X примет значение в интервале между xi и хг, равна

Р (*! < х < х„) = F (х₂) — F{x₁)=i_jf (х) dx. (2.1)

*»

В практике электрорадиоизмерений чаще всего имеют дело с нормальным и равномерным распределениями.

Случайная величина X распределена нормально, если ее плот­ность вероятностей имеет вид

__ (х—т)«

/(*) = ¹ е~ ²⁰¹ ,

' ’ оУ2я ’

где о — среднее квадратическое отклонение (ОКО), т = М[Х] — математическое ожидание.

Математическое ожидание Af[X] случайной величины X явля­ется постоянной величиной и характеризует ее среднее значение.

о

Величина А=Х—М[Х\ является случайной погрешностью. Если систематическая погрешность отсутствует, то математическое ожи­дание равно истинному значению величины X.

Рис. 2.1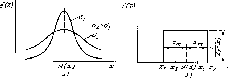

На рис. 2.1,а показана дифференциальная функция нормально­го распределения f(x). Видим, что с уменьшением о уменьшается рассеяние результатов вокруг X. При расчетах используют нор­мированное нормальное распределение, использующее нормиро-

о

ванную случайную величину t = A/a:

1 ^и

Интеграл Я(^) = — \е~^(1/2 dt выражает вероятность попада-

~[/2л о

ния случайной погрешности в интервал 0—ti и носит название функции Лапласа. Значения f(i) и P(ii) приведены в табл. 1 и 2 Приложения. Из табл. 2 Приложения, в частности, можно най­ти, что вероятность появления случайной погрешности в интерва­лах +^ = ±Ai/a = + l; +2; +3 с учетом симметричности распре­деления равна соответственно 0,683, 0,954, 0,997. Эти цифры ха­рактеризуют вероятность появления случайной погрешности 'в ин­тервалах ±<т; ±’2о; ±3а.

Нормальное распределение согласно центральной предельной теореме имеет сумма бесконечно большого числа бесконечно ма­лых величин с любым законом распределения. На практике сум­ма сравнительно небольшого числа (4-5) статистически независи­мых величин одного порядка имеет распределение, близкое к нормальному. Если случайные погрешности определяются по ре­зультатам измерений, то погрешности в большинстве случаев имеют нормальное распределение.

Равномерное распределение, показанное на рис. 2.1,6, аналити­чески записывается в виде:

Вероятность появления погрешности в интервале Xk—Xs очевидно равна P=J f(x)dx.

Примером случайной погрешности, имеющей равномерное рас­пределение, является погрешность отсчета по шкале прибора и погрешность квантования измеряемой величины по уровню в циф­ровых измерительных приборах. Равномерное распределение в пределах допускаемых границ приписывают погрешности измери­тельного прибора. Равномерное распределение принимают всегда, когда закон распределения неизвестен.

В практике электрорадиоизмерений встречаются и другие за­коны распределения. ГОСТ 8.011—72 указывает функции расп­ределения, которыми следует аппроксимировать реально имеющие место законы. Это нормальная, равномерная, треугольная, трапе­цевидная, антимодальные I и II, Рэлея. Отношения максимальной погрешности к СКО соответственно равны |е|/сг=3; 1,7; 2,4; 2,3; 1,4 и 1,2; 3,3.

Встречаются случаи, когда задача оценивания погрешности приводит к функции распределения, существенно отличной от ука­занных выше, так что ее неудобно аппроксимировать ни одной из них. В практике электрорадиоизмерений таким законом являет­ся, например, закон арксинуса (U-образное распределение).

Для характеристики случайных величин применяют также на­чальные и центральные моменты. Основными среди них являются математическое ожидание и дисперсия.

Математическое ожидание (первый начальный момент):

M[X] = Jxf(x)dx,

— 00

дисперсия (второй центральный момент):

D [X] = ](х— М [X])² f (х) dx.

— 00

Положительное значение корня квадратного из дисперсии и есть упоминавшееся выше среднее квадратическое отклонение (СКО) случайной величины о= Vd.

Математическое ожидание, как отмечалось, является центром, относительно которого группируются значения случайной величи­ны. СКО характеризует степень рассеяния значений случайной величины относительно математического ожидания.

Нормальное распределение полностью характеризуется мате­матическим ожиданием М[Х] и СКО о.

Равномерное распределение (рис. 2.1,6) тоже определяется двумя параметрами М[Х\ и x_m(Xi = M[X]—x_m, Хг=М[Х]+Хт)-

Дисперсия равномерного распределения

00

D[X}= l(x—MiX\)*f(x)dx=*

м [X] 2х_т 3

2 Хщ

а среднее квадратическое отклонение а=У"0[Х] = x_m/]/3.

Вероятность появления случайной погрешности в интервале ±о в соответствии с (2.1) составляет Р = а/х_т = 0,578.

В информационной теории измерений, развитой советским уче­ным П. В. Новицким, введено понятие энтропийного значения погрешности

(2.2)

Д,= ±—е^н<^), 2

• о

где Н (Д₀) =— £/(Д₀) In / (Д₀) d Д₀—энтропия случайной погреш-

—оо

ности, которое представляет собой значение погрешности с равно­мерным законом распределения, эквивалентное в отношении де­зинформационного действия погрешности с данным законом расп­ределения.

Энтропийные погрешности оказываются весьма близкими к практически используемым оценкам предельной погрешности, сни­мая, таким образом, неопределенность, связанную с выбором до­верительной вероятности. Для нормального распределения Д_э = = 2,07о₀, для равномерного Д_э=1,73ао. Для нормального распре­деления эта погрешность соответствует вероятности Р = 0,95, а для равномерного ■— Р=1.

Оценка случайных погрешностей прямых равноточных измере­ний. Случайные погрешности проявляются при многократных наб­людениях измеряемой величины в одинаковых условиях. Их влия­ние на результат измерения надо учитывать и стремиться по воз­можности уменьшать. Рассматривая математическое ожидание случайных величин, мы считали, что располагаем всей совокуп­ностью, т. е. бесконечным множеством значений этой величины. При измерениях, даже с многократными наблюдениями, естествен­но, располагают конечным множеством результатов наблюдений и реализаций случайной погрешности. Как же в таких условиях оценить истинное значение измеряемой величины и случайную погрешность? Математическое ожидание и дисперсия считаются неизвестными. Отвечая на этот вопрос, теория вероятностей рас­сматривает задачу о наилучшей оценке параметров распределения вероятностей при конечном числе реализаций.

К оценкам случайной величины, получаемым по статистическим данным, предъявляются требования состоятельности, несмещеннос­ти и эффективности. Оценка ¹параметраQ считается состоятель-

ной, если CKQi, Q2, Фп)'-»-фис* при л-»-сю, несмещенной, если

M[<3] = Qhct, эффективной, если Z}[Q]=min. Здесь Q* — результат t-ro наблюдения, л — число наблюдений.

Способы нахождения оценок конечного ряда наблюдений и по­казатели их качества зависят от законов распределения.

Для нормального распределения, а если поступиться эффек­тивностью оценки, то и для всех симметричных распределений, в качестве оценки математического ожидания ряда равноточных наблюдений принимают среднее арифметическое ряда наблюдений

П

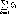
M{Q] = Q= ^Ql±^Q2+ _: + ^q" ==

П

п

п

п

1=1

При оо, если отсутствует систематическая погрешность, Q-*- -*~Qист. Разность Vi = Qi—Q представляет собой случайную пог­решность при i-м наблюдении. Она может быть положительной и отрицательной. Случайные погрешности, входящие в Q_u Q2, ..., Q_n, имеющие разные знаки, при суммировании взаимно уничтожают­ся. Среднее арифметическое независимо от закона распределения обладает следующими свойствами:

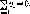
(2.3)

(2.4)

Свойство (2.3) используется для проверки правильности вы­числения Q, свойство (2.4) вытекает из принципа Лагранжа и по­ложено в основу широко используемого метода наименьших квад­ратов.

В качестве оценки дисперсии берется дисперсия отклонения результата наблюдения

П

5[Q[ = a²(Qi) = —г .

п 1

i=I

а в качестве оценки СКО результата наблюдения —

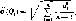
(2.5)

Подчеркнем, что формула Бесселя (2.5) характеризует сред­нее квадратическое отклонение (СКО) отдельного наблюдения. Поскольку мы вычисляем среднее арифметическое, которое необ­ходимо для получения оценки (2.5), то, естественно, взять его за результат измерения. Среднее арифметическое зависит от числа измерений и является случайной величиной, которая обладает не­

которой дисперсией относительно истинного значения величины-

Q ист.

В теории вероятностей показывается, что оценкой дисперсии среднего арифметического ряда наблюдений относительно истин­ного значения является

£[$]=>(ё)=5²(<?г)/л. (2.6)

Величина o(Q) =a(Q,)/|^ra=5 называется CKO результата изме­рений.

Таким образом, взяв за результат измерения Q, уменьшаем СКО в Vn раз по сравнению со случаем, если бы за результат измерения принималось любое одно из п наблюдений. Измерения с многократными наблюдениями и соответствующая обработка результатов позволяет уменьшить случайную погрешность и оце­нить ее. Оценки сг (Qi), о(ф) являются так называемыми точеч­ными оценками случайной погрешности. Они указывают интервал значений измеряемой величины, внутри которого находится истин­ное значение ф±о(ф). В отличие от точечной при интервальной оценке определяется доверительный интервал ер, в котором с до­верительной вероятностью Р находится истинное значение Q_Bст:

Е_р = ±tp(T(Q) .

При заданной вероятности Р и вычисленной o(Q) значение t_P определяется законом распределения. В случае нормального рас-

о

пределения и числа измерений п~^20 t_P = Alo выбирается по таб­лице функций Лапласа (см. табл. 2 Приложения), при этом зна­чения вероятности Р умножаются на 2, так как в табл. 2 они при­ведены для половины симметричного интервала.

Если число измерений га^20, доверительный интервал слу­чайной погрешности при заданных вероятности Р и СКО резуль­тата измерения o(Q) определяется по формуле Стьюдента е_р= ^ t_P._no (Q),

где t_P.n — коэффициент распределения Стьюдента, который зави­сит от заданной вероятности Р и числа измерений п (см. табл. 3 Приложения).

При п~^.20 распределение Стьюдента приближается к нормаль­ному и вместо t_P,n, можно использовать t_P для нормального рас­пределения. При равномерном распределении обычно принимают

е= ±1,73(t(Q), т. е. для Р= 1, поскольку доверительный интервал слабо зависит от доверительной вероятности. Таким образом, ис­тинное значение, очевидно, будет находиться внутри интервала:

Q—ер< Q ИСТ < Ф + ер.

Можно также выразить относительную случайную погрешность е_ор, соответствующую доверительной вероятности Р, %, как

е₀р= (ep/Q) 100.

Рассмотрим теперь, какую же доверительную вероятность сле­дует брать? Как правило, принимают Р=10,95. Если измерения нельзя повторить, то Р = 0,99, а в особо ответственных случаях, когда проводимые измерения связаны с созданием новых этало­нов или имеют значение для здоровья людей, и выше.

В этих случаях при нормальном распределении доверительный

интервал ep = 3a(Q), что соответствует доверительной вероятности Р = 0,997.

Остановимся еще раз на оценке закона распределения. Выше приводились соображения относительно причин, обусловливаю­щих то или иное распределение. Еще раз подчеркнем, если слу­чайные погрешности оцениваются по результатам измерения (а не по теоретическим соображениям), то, как правило, следует принимать нормальное распределение. Композиция двух центри­рованных равномерных распределений с границами ±Д_Ь ±Дг дает трапециевидное распределение с границами ± (| Ai | + | Дг|) и меньшим основанием, заключенным между точками ±(|Д]|— — | Д21). При Д1 = Дг=Д суммарное распределение представляет собой треугольное распределение с границами +2Л.

Из теории вероятностей известно, что, если проведено большое число наблюдений (га^ЗО), то оказывается возможным прове­рить гипотезу относительно закона распределения. Гипотеза мо­жет быть высказана на основе построения гистограммы.

Для проверки соответствия гипотезы экспериментальному рас­пределению существует ряд критериев. Наиболее распространен­ным является так называемый критерий Пирсона, или критерий X² («хи-квадрат»), который позволяет проверить соответствие экс­периментальных данных любому распределению, а не только нор­мальному. Этот вопрос рассматривался при изучении теории ве­роятностей. Подробно с ним можно ознакомиться, например, в [6].

Остановимся на способе исключения из результатов измере­ния промахов и грубых погрешностей. Если в полученной группе результатов наблюдений одно-два резко отличаются от остальных, то, прежде всего, следует проверить, нет ли описки, ошибки в снятии показаний или других промахов. Если промахи не установ­лены, то следует проверить, не являются ли они грубыми погреш­ностями. Эта задача решается статистическими методами, основан­ными на том, что распределение, к которому относится выборка, можно считать нормальным. Рассчитаны и сведены в таблицу q- процентные точки ¹распределения максимальных по модулю от­клонений результатов наблюдений от их среднего значенияt_r =

= max| Qi—Q|/o(Qj) в зависимости от числа наблюдений. Чтобы проверить возможность отбросить некоторое наблюдение Q_B, на­до сначала вычислить f=|Q„—Q\l<*(Qi). Затем, выбрав уровень значимости q, следует по табл. 4 Приложения найти значение #_г, отвечающее данным q и п. Если t>t_r, то Q_B можно отбросить. С уменьшением q растет t_r и условие t>t_T выполняется труднее.

Необходимо заметить, что при записи результата измерения и погрешности младшие разряды числовых значений результата из­мерения и числовых значений погрешности должны быть одина­ковы. Например, U—12,5 В, ер=±0,1 В, а не U= 12,52 В, ер= = ±0,1 В или [/=12,5 В, ер=±0,13 В.

Поскольку погрешности измерений определяют лишь зону не­достоверности результата, их не требуется знать очень точно. Погрешности оценок случайных погрешностей, особенно при ма­лом числе измерений (л^Ю), весьма велики. Поэтому погреш­ности измерения в окончательной записи принято выражать чис­лом с одной или двумя значащими цифрами. При промежуточных выкладках в числовых значениях погрешности необходимо удер­живать по три-четыре значащих цифры, чтобы погрешности округ­ления не искажали результат.

Схема обработки результатов измерения с многократными наб­людениями приведена на рис. 2.2.

Рис. 2.2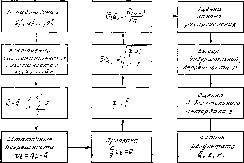

Оценивание случайной погрешности расчетным путем. Рассмот­рим случай, когда случайная погрешность и ее границы могут быть оценены расчетным путем. Это имеет место при отсчете экс­тремума или заданного уровня некоторой величины. Понятно,

что границы случайной погрешности определения экстремума мо­гут быть оценены экспериментально многократными наблюдения­ми и соответствующей обработкой результатов, как это показано выше. Однако при априорной оценке погрешности, планировании измерений оказывается очень полезным оценить случайную пог­решность расчетным путем.

Пусть зависимость показаний прибора а от измеряемой вели­чины Q имеет вид a=f(Q) (р»с. 2.3,а,б). Требуется определить погрешность измерения AQ, обусловленную конечной разрешаю­щей способностью отсчетного устройства Да. Очевидно, отличие а от экстремального значения а_э равновероятно в интервале от О до Да. На рис. 2.3 видно, что измеряемая величина при этом может иметь значения от Q до Q±AQ. Погрешность AQ будет иметь распределение, зависящее от вида функции f(Q). Опреде­лим границы погрешности AQ.

ат

Or О ₃ Oz а)

Or Oq Оz О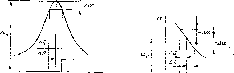

Or 0₃ 0.2

а

6)

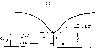
Рис. 2.3

Разложив функцию a = f(Q) в ряд Тейлора в окрестности точ­ки экстремума, т. е. при Q = Q₃, отбросив члены с производной выше второй, можно получить:

Учитывая, что df/dQ — О при Q = Q₃, получаем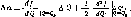

(2.7)

Д Q = У 2 Да/d² / (Q)/dQ²

и е= ±ДС? при Р = 1.

Получили формулу, связывающую границы случайной погреш­

ности измерения е экстремального значения Q₃ и разрешающую способность прибора Да. Закон распределения может быть оценен на основе соображений, изложенных выше. Заметим, что разре­шающая способность аналоговых отсчетных устройств составля­ет 0,2 ...0,5 делений.

Оценим теперь границы случайной погрешности индикации заданного уровня а. Из-за конечной разрешающей способности отсчетного устройства Да возникает погрешность определения уровня а₀ и соответствующего ему значения измеряемой величи­ны Q₀ (см. рис. 2.3,в). Поскольку заданный уровень отсчитыва­ется вблизи точки перегиба кривой f(Q), где наибольшая крутиз­на, вторая производная равна нулю и разложение a = f(Q) в ряд Тейлора вблизи заданного уровня запишется, как

df (Q)

dQ

а = f (Q₀) 4" ■

Д Q.

Q=Qo

Разность a—f (Qo) обусловлена конечной разрешающей способ­ностью индикатора и равна Да. Следовательно, AQ = ——— и

df(Q)/dQ

е= ±AQ при Р = 1.

3. СПОСОБЫ ОЦЕНИВАНИЯ И ИСКЛЮЧЕНИЯ СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ

Общие замечания. Как указывалось выше, оценить и исклю­чить систематические погрешности, т. е. погрешности, которые ос­таются постоянными или закономерно изменяются при повторных измерениях в одинаковых условиях, способом многократных наб­людений нельзя. Результат одного наблюдения можно записать, как

Qi^{, =} QiicT + At + Ac,

•

где Д,- — реализация случайной погрешности, А_с — постоянная систематическая погрешность.

Если провести п наблюдений и взять среднее арифметическое, го будем иметь

П

^ А;

Q=-<2i,ct + ——Ь^с-

п

Из-за различных знаков реализаций случайной погрешности случайная составляющая с ростом п уменьшается, а системати­ческая будет оставаться неизменной. Систематическая погреш­ность измерений редко может быть определена целиком, а не сум­мированием отдельных составляющих. Это можно осуществить, если выполнить измерение более точным методом с использовани­ем более точных средств измерений. Значительно чаще приходит­

ся находить составляющие систематической погрешности, а затем их суммировать. Для этого необходимо глубоко понимать прин­цип работы средств измерений и физические процессы, протекаю­щие в измерительных цепях. Полностью исключить систематичес­кую погрешность введением поправки нельзя, поскольку поправ­ка также определяется с некоторой погрешностью. Таким обра­зом, всегда остаются неисключенные остатки систематической пог­решности (НСП), которые обычно рассматриваются как случай­ные.

Заметим, что систематические погрешности могут быть связа­ны с каждым из элементов процесса измерений: несовершенством модели объекта измерения, несовершенством метода, средством измерения, изменением внешних условий, личными качествами наблюдателя.

Общие способы оценивания и исключения систематических погрешностей. Для обнаружения, оценки и исключения системати­ческих погрешностей требуется тщательное изучение применяемых конкретных методов, средств, условий измерения. Однако можно указать простейшие общие способы обнаружения, оценки и иск­лючения систематических погрешностей.

1. Исключение систематической погрешности при измерении путем применения соответствующих методов и приемов, например метода замещения (см. § 3.2), метода компенсации погрешности по знаку, использующего два измерения, в результаты которых систематическая погрешность входит с разными знаками и др. Эти методы позволяют исключить постоянную систематическую погрешность, обнаружение которой представляет наибольшие трудности, непосредственно в процессе измерения, а не путем об­работки результатов.

2. Оценка систематической погрешности путем применения бо­лее точного метода и средства измерения.

Систематическая погрешность, если пренебречь погрешностью сличения, будет равна A_C = Q—Qt, где Q_T — результат точного из­мерения.

3. Обнаружение систематической погрешности в результатах измерений с многократными наблюдениями одной физической ве­личины двумя независимыми методами. Для этой цели разработа­ны статистические методы обработки результатов, методы корре­ляционного и регрессионного анализа.

4. Оценивание систематической погрешности расчетным путем. Для этой цели выражают значения измеряемой величины с уче­том влияющего фактора («измеренное значение») и при его от­сутствии («истинное значение»). Разность первого и второго зна­чений и будет абсолютная систематическая погрешность Д_с= ⁼ Qh3M Q ист-

В качестве простейшего примера оценим погрешность при измерении пос­тоянного электрического тока, обусловленную сопротивлением амперметра. Обозначим г_г — внутреннее сопротивление источника, Я— сопротивление нагруз- «и, га — сопротивление амперметра, е — ЭДС источника, а /жзм — измеренное значение тока. Тогда 1жзи=е1(Я+г_г+гл), а /жст=е/(R+r_r). Абсолютная систе­матическая ПОгреШНОСТЬ Дс=/жам—/жст = —/жзиГа/(/?+Г_г).

5. Исключение систематической погрешности введением поп­равки. Поправка С = —Д_с бывает известна с ограниченной точ­ностью и характеризуется средним значением С со СКО а (С). При введении поправки систематическая составляющая погреш­ности уменьшается, а дисперсия результата измерения возраста­ет. Критерием целесообразности введения поправки является ин­тервал суммарной погрешности измерений. Если поправка не вве­дена, интервал суммарной погрешности составляет C+t_Pa(Q),

если введена —/piKo² (Q) -f а²(С). Здесь ar(Q) и а(С) — оценки средних квадратических значений случайных погрешностей ре­зультата измерений величины Q и поправки С, а t_P и t_Pi — ве­личины, зависящие при одинаковой доверительной вероятности

о О в

от законов распределения Д(<2) и A(Q)+A(C). Поправку необхо­димо вводить, если

C + t_Po(Q)> tpiV"a² (Q) -fa² (С).

Отсюда получаем условие целесообразности введения поправки при t_P = t_Pi

С > t_P a (Q) [V1 + a² (C)/a² (Q) -- 11. (2.8)

(Вызод условия (2.8) следует рассматривать после изучения § 2.4.)

Формы выражения систематической погрешности. При оценива­нии систематических погрешностей задача может ставиться по- разному. Можно ставить задачу оценить систематическую погреш­ность для данного измерения — конкретного метода и конкрет­ного средства измерения. В этом случае систематическая погреш­ность зыражается постоянным числом в единицах измеряемой ве­личины со своим знаком. Если же повторить измерение тем же методом, но с использованием других средств измерения, система­тическая погрешность может иметь другое значение. Для множе­ства возможных измерений величины тем же методом, но с ис­пользованием множества средств измерений того же типа, систе­матическую погрешность в ряде случаев можно рассматривать как реализацию случайной погрешности и представлять ее как слу­чайную: в форме доверительного интервала и соответствующей доверительной вероятности в зависимости от функции распреде­ления. Однако функцию распределения строго обосновать затруд­нительно. Определяются лишь границы систематической погреш­ности. Если известно, что конкретный измерительный прибор име­ет допустимую систематическую погрешность ±1%, то это зна­чит, что его погрешность находится в границах ±1%. которые ха- растеризуют совокупность приборов данного типа. Конкретный экземпляр прибора может иметь и меньшую погрешность.

Итак, систематическая погрешность очень часто может быть представлена границами, чаще всего симметричными. Если обос­новать функцию распределения вероятностей, то систематическую погрешность можно представить как случайную, определить для нее и соответствующий доверительный интервал. Такие система­тические погрешности называются квазислучайными.

Для каких целей это делается? Во-первых, случайные погреш­ности, если известны их дисперсии, могут обоснованно суммиро­ваться. Необходимо только оценить закон распределения суммар­ной погрешности. Ранее указывалось,’ что при 4-5 примерно оди­наковых слагаемых распределение оказывается весьма близким к нормальному. Во-вторых, систематические погрешности, вообще говоря, должны быть исключены. Но поправки имеют ограничен­ную точность, так что, в конце концов, дело сводится к оценива­нию случайной погрешности. В-третьих, представление система­тической погрешности в форме случайной позволяет оценить до­верительную погрешность в общем случае использования не кон­кретного средства измерения, а любого из совокупности средств измерений данного типа, что очень важно при разработке техни­ческой документации.

Если известны границы систематической погрешности и нет оснований для того, чтобы приписать тот или иной закон распре­деления, принимается равномерное распределение. Так в подав­ляющем большинстве случаев и поступают.

Но в некоторых случаях удается обосновать функцию распре­деления. Рассмотрим в качестве примера систематическую пог­решность вида

A_c = asinqp, (2.9)

которая часто встречается в практике электрорадиоизмерений (действие синусоидальной помехи; погрешность от опрокидывания в подвижной части электроизмерительных приборов на кернах вследствие зазора между керном и подпятником; погрешность, обусловленная отражением от несогласованной нагрузки при из­мерениях на СВЧ и т. д.). Измерять фазу <р для оценки этой пог­решности лишено смысла, поскольку при измерении в несколько других условиях (например, при изменении длины тракта СВЧ) фаза ф и погрешность Д_с будут иметь другие значения. Поэтому все значения фазы считают равновероятными. Фазу рассматрива­ют как случайную величину, распределенную равномерно в гра­ницах ±я/2, поскольку границы систематической погрешности 0 = — ± а.

Какова будет функция распределения систематической погреш­ности Д_с? Поскольку этот пример имеет значение при изучении способов учета систематических погрешностей, рассмотрим общий случай функции y=ty(x). Обозначим f(x) — плотность распреде­ления вероятностей случайной величины х, g(y) — плотность

распределения вероятностей случайной величины у, a F\x) и G(y) соответственно их функции распределения. Тогда вероятность на интервалах Дх и Ду можно записать

F (лт+Длг) —F (*) =f(x)Ax=G(y+Ay)—G (у) =g(y)Ay. При Дх-»-0 имеем

(2.10)

g(y)=f(x)dxldy=f{x)W{x).

Формула (2.10) позволяет установить связь между плотностями вероятностей аргумента х и функции у.

В нашем примере

/(ф) = 1/л при —л/2^ф^я/2,

/(ф)=0 при ф<л/2 и ф>л/2.

Дифференцируя (2.9) и подставляя в (2.10), получаем для ин­тервала ф = ±я/2

g(Д_с) = 1/яя cos ф.

Выражая соэф через эшф и далее через Д_с, находим

(Дс) ⁼ 1/я а² Д²_С, —я^Д_сй^1 -f- я;

g (Дс) ⁼ 0, Д_с<—я и Д_с^>+я.

I

/

Получили плотность распреде­ления вероятностей систематиче­ской погрешности Д_с. Это распре­деление носит название U-образ- ного или распределения по закону арксинуса (рис. 2.4).

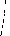
Среднее квадратическое откло­нение можно рассчитать по фор­муле

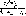
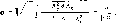
Рис. 2.4 У _₀ я у с

ul il 1 •

я а

. At

arcsin —

а

Например, для интервала ±Ai = ±af2 доверительная вероят­ность составит Р = 0,33.

Подобным образом могут быть переведены в разряд случайных многие другие систематические погрешности: частотные, темпера­турные и т. п. Этот путь позволяет не определять погрешности для каждой частоты диапазона, а, задавшись равномерным рас­пределением частоты в заданном частотном диапазоне, опреде­лить распределение вероятностей погрешности, обусловленной из-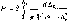

а доверительная вероятность интервала +Ai равна

менением частоты, а также числовые параметры этого распреде­ления.

4. ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ.

СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ

Общие выражения для оценки результата и погрешностей. Вы­ше, в § 1.2, уже было дано определение косвенного измерения. Здесь задача будет состоять в том, чтобы получить оценку ре­зультата 0 и погрешности Д косвенного измерения, имея оценки результата ф» и погрешности Д; прямых измерений каждого из аргументов. Этот воспрос тесно связан с изучением методики ана­лиза погрешностей измерения, с вопросами суммирования случай­ных и систематических погрешностей, включая суммирование пог­решностей при прямых измерениях, что не было рассмотрено ра­нее.

Пусть каждый из аргументов Q¹характеризуется оценкой <3,-

О

и погрешностью Д* = Д_Сг + Дь которая представляет собой некую реализацию суммарной погрешности i-ro аргумента. Подставим в уравнение косвенного измерения (1.1) величину Qi = Qi+Aj. Раз­лагая функцию в ряд Тейлора и пренебрегая членами со степеня­ми выше первой, имеем

Q = f(Q_u Q₂, ..., Q_m) = f(Q_u Q_If.... QJ + S 4^^A‘- ^(2Л1)

fil dQi

Отсюда получаем оценку результата *

Q = f(Ql> <22. <2m) (2.12)

и погрешности косвенного измерения

д-1 ₍₂.₁₃)

(=1 “V; ,-₌₁

Производные Wi = df/dQ_t называются коэффициентами влия­ния, а слагаемые W{Aг — частными погрешностями.

Рассмотрим случайные погрешности. При этом реализация сис­тематических составляющих погрешностей оценок всех Q, будем считать постоянными. Выразим оценку среднего квадратического значения случайной погрешности результата косвенного измере­ния, используя (2.12):

5 (А)²=D [Q] = 1/"^Wi.St+jlPvW^SbSt, (2.14)

V i=i k^i

где Si² — оценка дисперсии результата прямого измерения /-го

fiiQkj—QdiQu—Qi)

аргумента, Ры""— —— оценка коэффициента кор­ей/ о)

реляции между случайными погрешностями измерения аргумен­тов & и I. Коэффициент корреляции определяет степень связи меж­ду случайными величинами. Возможные значения коэффициента

корреляции лежат в интервале от —1 до +1. Если ры=0, то слу­чайные погрешности статистически независимы. В этом случае

S (/5) =* Щ ^sr (2.15)

Если же |рй(| = 1, то между результатами измерений Q_kj и Qij существует функциональная связь.

Заметим, что при суммировании следует пользоваться крите­рием ничтожности погрешностей; если WiSi^3WgSz, то W2S2 мож­но пренебречь.

Когда измерения аргументов проводят не одновременно и при этом используют разные по устройству средства измерений, нет оснований ожидать появления корреляции между погрешностями этих измерений.

Коэффициент корреляции определяется экспериментально по результатам многократных наблюдений аргументов Qb и Q_u Наи­более удобной формулой для определения коэффициента корре­ляции, которая связывает непосредственно результаты п наблю­дений Q_k и Q; без необходимости предварительного вычисления Qh и Qi, является приближенная формула

^л2 Qm Qu— 2 Qv 2 Qu

(2.16)

р_Л1 — ^/=1—

/=1 \ /=1

/-1 ' /=1

Выражения (2.14) и (2.15) могут быть использованы для оцен­ки СКО результата косвенного измерения для случая, когда Q* представляют собой результаты одиночных измерений с проведен­ной ранее оценкой СКО ряда наблюдений o(Qa):

ЭЛЕКТРОРАДИО­ИЗМЕРЕНИЯ 1

Москва «Радио и связь» 1985 2

/(*) = 1 е~ 201 , 17

МаЬЫг;.: 48

^лг;+„(,Л/(,+|)- «МО 198

Kr=V и\ ' (10-4> 324

t/2=^|£n|2[l+|r|2+2|r|cos(?-n/46)], 385

0 = arctg[lin(,p + (w/4)6)1 [sin (ф— (я/4) 6)J 386

f-i

Реализации неисключенных систематических погрешностей рассматривают по совокупности возможных измерений как реали­зации случайных погрешностей и для их оценивания используется

(2.17).

Оценку доверительного интервала и доверительной вероятнос­ти случайной погрешности, границ систематической погрешности, а также суммарной погрешности рассмотрим несколько позже.

Относительные погрешности косвенных измерений. Распрост­раненным видом уравнения измерения является

Q = Qi^ftQ₂^I...Qm". (2.19)

Оценка результата косвенного измерения производится по фор­муле (2.12), а реализация абсолютной погрешности по (2.13). Вы­разим относительную погрешность результата косвенного измере­ния. Вычислим коэффициенты влияния:

«Qi

W_t = -^- = QUQt^l...Qⁿ_m, (2.20)

dQ%

W_m = ^- = Q\Qi-nQⁿ~^ d Qm

Подставляя (2.20) в (2.18) и деля обе части на Q, получаем искомую относительную погрешность

б = —Н + ••• + ДГ²" ⁼ кЬ_г-\-1 б₂ +... +габ_т.

v vi v2 vm

Практический прием нахождения коэффициента влияния при выражении погрешностей в форме относительных погрешностей состоит в том, что уравнение измерения сначала логарифмирует­ся, а затем дифференцируется.

Оценка относительного СКО результата косвенного измерения, очевидно, выразится, как

s_B{A)=^L= 1 > s-_m + +... + п* si_т,

Q

где Soi = Si/Qi — относительная оценка СКО результата измере­ния Qi.

Для электрорадиоизмерений представляет интерес рассмотреть функцию вида Q = Qi—Q2. Применяя формулу (2.14), имеем

S(A) = KS2 + S2-2p,.₂S₁S_r

Когда коэффициент корреляции pi,2=l, то величины Qi и Q₂ связаны функционально:

5 (Д) = VSf+Щ-25757= - S,.

2- 94 33

° о

Если 5i = 5₂=5, то S(A)=0. В остальных случаях S(A)=?^0. Поэтому при измерении и вычислении малых разностей рекомен­дуется найти значение ры-

Относительная погрешность 5₀(Д) = S(A)/<3=S(A)/(<3i—Q₂). Можно видеть, что при малых значениях разности <3i—<3г пог­решность может приобретать очень большие значения.

Общая задача при косвенных измерениях состоит в разработ­ке таких методов, которые обеспечивали бы сохранение в допус­тимых пределах погрешности косвенного измерения. Это достига­ется: 1) выбором значений Q; и Q&, при которых относительная погрешность не выходит за пределы допустимой; 2) применением таких способов измерения, при которых уравнение косвенного из­мерения не содержало бы малых разностей; 3) разработкой та­ких методов и средств измерений, которые бы обеспечивали пря­мое измерение вместо косвенного.

Определение доверительного интервала случайной и границ неисключенной систематической погрешностей. Формулы (2.14) —

18. описывают закономерности суммирования погрешностей при косвенных измерениях. Если уравнение измерения имеет вид Q — = Qi + Q2+ ... +Qm, то получение абсолютной погрешности косвен­ного измерения совпадает с задачей суммирования погрешностей прямых измерений. Действительно, для этого случая реализация абсолютной погрешности освенного измерения будет A = Ai+A₂ + -t- ... -hA_m; так же будет выражаться и реализация погрешности прямого измерения. Разница будет состоять в том, что А, в пер­вом случае представляет собой реализацию погрешности измере­ния г-го аргумента, но втором А? — реализация одной из пог­решностей измерения величины Q. Таким образом, закономернос­ти суммирования погрешностей в этих случаях будут общими. Наша задача теперь будет состоять в том, чтобы рассмотреть, как оценивается доверительный интервал случайной погрешности и границы или доверительный интервал неисключенных системати­ческих погрешностей результата косвенных измерений.

Случайную погрешность результата косвенного измерения, об­разующуюся путем сложения случайных погрешностей результа­тов измерений аргументов, можно считать нормально распреде­ленной случайной величиной, поскольку слагаемые имеют нор­мальные распределения. Даже если слагаемые имеют распределе­ние, отличное от нормального, но число слагаемых не менее 4-5 и отсутствует доминирующая погрешность, распределение случай­ной погрешности косвенного измерения можно считать нормаль­ным.

Доверительные границы ер случайной погрешности определя­ются по формуле ep=i£pS(A).

Коэффициент tp=2i_P/2, где t_P/2 находится по таблицам функ­ции Лапласа (табл. 2 Приложения).

Выше говорилось, что реализации неисключенных системати­

ческих составляющих по совокупности возможных аналогичных измерений можно рассматривать как реализации случайной ве­личины. Для каждой из составляющих находят границы 0_t-. Если в этих границах можно обосновать закон распределения и оце­нить о (А_с), то границы неисключенных остатков систематических погрешностей результата косвенных измерений можно определить

по формуле 0=Д_Ро(Дс).

Если известны только границы 0,-, а распределение предпола­гается равномерным, то границы неисключенных остатков систе­матической погрешности результата косвенного измерения мож­но вычислять по формуле

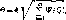
(2.21)

где k — коэффициент, определяемый принятой доверительной ве­роятностью.

При доверительных вероятностях 0,9; 0,95; 0,99 коэффициент k соответственно равен 0,95; 1,1; 1,4.

Очевидно, при определении границ неисключенных системати­ческих погрешностей прямых измерений в (2.21) надо положить

Wt= 1.

Границы суммарной погрешности измерений в соответствии с

ГОСТ 8.207—76 оцениваются следующим образом. Если 0/5 (Х)< <0,8, то неисключенными систематическими погрешностями пре­небрегают и граница погрешности результата принимается равной

Д_г=е. Если 0/5(Д) >8, то пренебрегают случайной погрешностью и границы принимают равными Д₂ =0. Если же эти неравенства не выполняются, то необходимо найти композицию распределе­ний случайных и неисключенных систематических погрешностей,

рассматриваемых как случайные величины, определить a_z и гра­ницы суммарной погрешности A_z = t_sa_z.

Допускается определять границы суммарной погрешности по формуле Ах — k_z S_z,

При оценивании погрешностей измерений по однократном из­мерениям, выполненным измерительными приборами, имеющими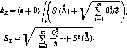

где k_z— коэффициент, зависящий от соотношения случайной и систематической погрешностей, 5х — оценка суммарного СКО результата измерения,

пределы допускаемой погрешности A_f, границы погрешности рас­считывают по формуле (2.2:1).

Погрешности, обусловленные расчетом на ЭВМ. Для обработ­ки данных измерений в настоящее время широко используются ЭВМ. Использование ЭВМ открывает большие возможности для повышения точности и уменьшения трудоемкости такой обработ­ки. Вместе с тем при использовании ЭВМ необходимо учитывать погрешности, обусловленные параметрами ЭВМ и их програм­мным обеспечением.

Различают три вида погрешностей, связанных с обработкой данных на ЭВМ: погрешности преобразования исходной информа­ции в цифровую форму, погрешности ограничения процесса вы­числений конечным числом операций, погрешности округления.

Преобразование измерительной информации в цифровую фор­му связано с процессом дискретизации и квантования аналогово­го сигнала, выбором соответствующего шага дискретизации и ша­га квантования.

Погрешность ограничения процесса вычислений обусловлена используемым численным методом решения данной задачи. Мно­гие процессы вычислений являются бесконечными. Поэтому ана­лиз погрешности ограничения очень важен.

Погрешность округления возникает вследствие того, что в ЭВМ число представляется некоторым количеством значащих цифр. Если исходные данные или результат вычислений имеют больше цифр, то они округляются. Погрешность округления долж­на быть оценена.

Расчет статистических характеристик на ЭВМ не вызывает трудностей, поскольку приведенные в § 2.2 формулы сводятся к простейшим прямым вычислениям. Накопление погрешностей не возникает, так как нет необходимости получать решение с высо­кой точностью. Благоприятная структура расчетных формул при­водит к том}', что даже при очень больших выборках погрешность округления не достигает опасных уровней. С помощью ЭВМ мож­но осуществить построение гистограмм и проверку гипотез о за­коне распределения. Имеются стандартные программы подготовки гистограмм, которые входят в математическое обеспечение ЭВМ. Особенно эффективно могут использоваться ЭВМ при наличии графопостроителей, с помощью которых гистограмма может не­посредственно печататься машиной.

Погрешность, обусловленная расчетом на ЭВМ, обычно не пре­вышает (2 ... 3) • 10~² % •

5. ФОРМЫ ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИИ И ПОКАЗАТЕЛИ ТОЧНОСТИ

Чтобы результаты, полученные в различных лабораториях, могли сопоставляться, формы представления результатов измере­ний и показатели- точности регламентируются нормативными до­кументами. В настоящее время действует ГОСТ 8.011—72 «По­казатели точности и формы представления результатов измере­ний».

Согласно этому стандарту результат измерения представляется в виде значения величины Р и показателей точности. В зависи­мости от сложности и ответственности измерений используются показатели точности измерения различной сложности. В качестве показателей точности установлены:

интервалы, в которых с заданной вероятностью находится сум­марная погрешность измерения Д или ее систематическая сос­тавляющая Д_с; „ о

оценки среднего квадратического значения случайной о(Д) и

систематической <т(Д_с) составляющих погрешностей;

плотность распределения систематической или случайной сос­тавляющих погрешностей /(Д_с) и ^(Д).

Наиболее распространены технические измерения, которые вы­полняются однократно. Их погрешность определяется погреш­ностью средства измерений. Эта погрешность известна до изме­рения из нормативно технической документации. Записывается результат измерения и погрешность в виде предела допускаемой суммарной погрешности. Вероятность не указывают предполагает­ся ее значение Р=0,997.

Погрешность в окончательной записи, как указывалось выше, принято выражать числом с одной или максимум двумя знача­щими цифрами. Две цифры удерживают при точном оценивании погрешностей, а также если цифра старшего разряда числа, вы­ражающего погрешность, равна прем или меньше трех, например, 0,23, но 0,6. При приближенном оценивании погрешностей, когда погрешность выражают одной значащей цифрой, цифру 9 не при­меняют, а две значащие цифры сохраняют, если цифра старшего разряда меньше трех, при этом для младшего разряда обычно применяют только цифру 5. Например, 0,25; 0,15; 0,8; 1,0.

Еще раз подчеркнем, что при промежуточных выкладках в числовых значениях погрешностей необходимо удерживать по три- четыре значащих цифры, чтобы погрешности округления значи­тельно не искажали окончательный результат.

Числовое значение результата измерения должно быть пред­ставлено с учетом погрешности, с которой это измерение выпол­нено. Младший разряд результата должен соответствовать раз­ряду погрешности.

В заключение главы обратим внимание на важное обстоятель­ство. Погрешности измерения классифицировались по характеру проявления на случайные и систематические. На этой классифи­кации основана нормативно-техническая документация, касающая­ся оценивания погрешностей. Однако, как мы видели, на практи­ке для исключения систематических погрешностей вносятся поп­равки, а неисключенные остатки рассматриваются как случайные. В ряде случаев систематическую погрешность можно учесть, ис­пользуя вероятностно-статистические модели. Все это противоре­чит определению систематической погрешности как неслучайной величины.

На 70-й сессии Международного Комитета мер и весов (МКМВ) в 1981 г. принята рекомендация пересмотреть установившееся де­ление составляющих погрешностей на случайные и системати­ческие. Рекомендуется классифицировать погрешности по способу их определения. Классификационным признаком при этом служит возможность или невозможность определения составляющих ста­тистическими методами. Рекомендация МКМВ изучается метро­логами всех стран.

Пока упомянутая рекомендация не нашла отражения в норма­тивно-технической документации.

В заключение в качестве упражнения рассмотрим практические при­меры оценки погрешностей и их записи.

1. Правильно ли записаны результаты измерений и погрешности?

1. 85,6342 В, Д=0,04 В, Я=0,952;

2. 85,63 В, Д от —0,04 до +0,04 В, Р=0,95;

3. 74,725 В, Д=±0,015 В, Р=0,95;

4. 50,7 Вт, 6 = ±0,7%, Я=0,99.

2. В таблице приведены результаты наблюдений при прямом измерении на­пряжения источника с помощью потенциометра. Определите оценку результата измерения и границы случайной погрешности. Систематические погрешности из показаний исключены.

в: о 2 Ч •2 2	Показания, В	ОС X •J ..о ^ я	Показания, 3	Номер наблюдения	Показания. В	!Я Я о < гг 2 §« *2 я	Показания, В
1	2.7997	9	2,7990	17	2,8011	25	2,7993
2	2,7991	10	2,7989	18	2,7988	26	2.7988
3	2,7990	и	2,7987	19	2,7999	27	2,7993
4	2,7997	12	2,7993	20	2,7993	28	2,7988
5	2,7992	13	2,8000	21	2,7998	29	2,7999
6	2,7986	14	2,7995	22	2,7996	30	2,7997
7	2,7984	15	2,7992	23	2,7992
8	2,7999	16	2,8006	24	2,7996

3. Проведено измерение силы тока, мА: 10,07; 10,08; 10,10; 10,12; 10,13; 10,15; 10,16; 10,17; 10,20; 10,40. Наблюдение 10,40 резко отличается от осталь­ных. Нельзя ли его отбросить как содержащее грубую погрешность?

4. Проведено однократное измерение мощности: 0,51 Вт. Оцените случай­ную погрешность этого измерения, если ранее проведенное измерение с мно­гократными наблюдениями близкой по значению величины дали результаты (Вт); 0,62; 0,59; 0,61; 0,58; 0,59; 0,58 и известно, что случайная погрешность не зависит от уровня измеряемой величины.

5. С какой целью систематические погрешности представляются как случай­ные?

6. Определите доверительную вероятность интервала ±а при равномерном и U-образном (арксинус) распределении.

7. Напряжение источника, имеющего внутреннее сопротивление Рг=(60± ±10) Ом, составило по показанию вольтметра с допускаемой погрешностью 0,5% 12,35 В на пределе 15 В. Сопротивление вольтметра R_v =5 кОм с до­пускаемой погрешностью ±0,5%. Определите систематическую погрешность, обусловленную шунтирующим действием вольтметра. Введите поправку. Оце­ните неисключенный остаток систематической погрешности.

8. Оцените суммарную погрешность прямых измерений частоты, если из­вестно, что оценка СКО результата измерения, выполненного по семи наблюде­ниям, составила 12 Гц, а границы неисключенного остатка систематической погрешности 0 = ± 18 Гц, Р=0,95.

9. Оцените погрешность косвенного измерения мощности по результатам прямых измерений тока и сопротивления. Границы суммарной погрешности из­мерения тока и сопротивления составляют 6j = 0,5%, бд=1°/о.

Ответы. 2. £7=2,7994 В, е=±0,0002 В, Р=0,95, норм. 3. 7=10,16 мА,

0(7.) =0,09 мА, £ = 2,25, £_г = 2,62. Наблюдение /=10,40 мА отбросить нельзя.

4. a[Pi) = j/s v]/(n — l) = 0,013 Вт, е = ±20(Р;) =0,026«0,03 Вт,

Р— 0,95. 6. Ррави = 0,58, Parcsin =0,5.

7. Относительная систематическая погрешность, обусловленная шунтидую- щим действием сопротивления вольтметра

и*

■и

_и

«с =

и_а

= —Ril(Ri + R_V) = —60/5060= —0,012;

абсолютная погрешность Д_с = —бс^' = —0,012-12,35 = —0,146 В, поправка с = = =0,146 В~0,15 В; скорректированный результат U_y— U — с= 12,50 В; аб­

солютная погрешность поправки

и =	' ARt	ARV	Rt '
	. RV	Rv	Rv

Г д б_с д б_с

U.

Д Rt

Поскольку

U,

ДР»/Ру> AR_v/R_Vy Ac-

границы неисключенного остатка систематической погрешности 0» 4^’ £/ = ±0,03 В.

Ку

т F б¹•Г18²

*₂ =

-у + 5⁸(Д) = у -3-+ 12*- 15,9 Гц; е + 0 12-2,36+18

12+ 18/1,73

= 2,07.

5(Д) + е/уз

9. Считаем, что распределение фактических суммарных погрешностей изме­рения тока и сопротивления равномерно в границах ±6/ и ±5_Л. Границы отно­сительной погрешности косвенного измерения (Р=0,95)

6_Р = А}/ (2 8^ + 6²_я = 1 >5%.