19.6. Адаптивный следящий фильтр

Описанный в предыдущем подразделе эксперимент можно, кроме того, использовать для иллюстрации еще одного важного приложения адаптивного устройства подавления помех. Во многих случаях, когда имеется входной сигнал, состоящий из смеси периодического и полосового сигналов, представляют интерес периодические, а не полосовые составляющие. Если выходной сигнал системы на рисунке 19.6. снимается с адаптивного фильтра, то в результате имеем адаптивный следящий фильтр, который может выделять из широкополосного шума периодический сигнал.

На рисунке 19.8. показана схема адаптивного устройства подавления в качестве следящего фильтра.

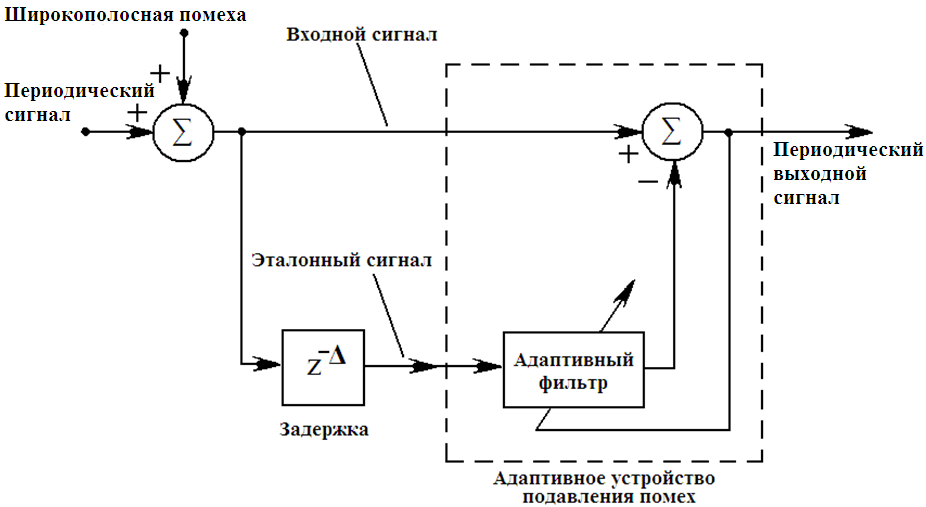
Рис. 19.8. Схема адаптивного устройства подавления помех в качестве следящего фильтра

Выходной сигнал этой системы получен с помощью моделирования на ЭВМ для входного сигнала из предыдущего примера (рис. 19.7,а). Действительный входной синусоидальный сигнал и полученное в результате адаптации его приближение показаны на рисунке 19.9. Здесь сигнал ошибки представляет собой случайный процесс с малой амплитудой.

На рисунке 19.10 приведены импульсная характеристика и передаточная функции адаптивного фильтра после сходимости.

Импульсная характеристика (рис. 19.10,а) близка к синусоидальному сигналу. При полосовой входной составляющей оптимальное устройство приема является согласованным фильтром, а его импульсная характеристика имеет синусоидальную форму.

Приведенная на рисунке 19.10,б передаточная функция равна дискретному преобразованию Фурье от импульсной характеристики. На частоте помехи ее амплитуда близка к единице – значению, требуемому для полного подавления. Сдвиг фазы на этой частоте не равен нулю, но при сложении с фазовым сдвигом, вносимым задержкой Δ, приводит к суммарному сдвигу на 360°.

Рис. 19.9. Входные сигналы системы подавления помех в качестве следящего фильтра

Рис. 19.10. Экспериментальные характеристики адаптивного следящего фильтра:

а) импульсная характеристика адаптивного фильтра после адаптации;

б) АЧХ адаптивного фильтра после адаптации

Аналогичные эксперименты проведены для сумм синусоидальных сигналов и широкополосной случайной помехи. В этих экспериментах адаптивный фильтр имеет резонансы на всех частотах, на которых во входном сигнале расположены периодические спектральные составляющие. Таким образом, эту систему можно использовать в качестве автоматического устройства поиска.

19.7. Адаптивный накопитель

Адаптивный следящий фильтр можно использовать в качестве накопителя при обнаружении в шуме синусоидальных сигналов с очень низким уровнем.

Адаптивный следящий фильтр, который, как показано выше, обладает свойством разделять в сигнале периодические и случайные составляющие (когда их уровни сравнимы), при обнаружении в шуме синусоидального сигнала с очень низким уровнем может работать как адаптивный накопитель. Это адаптивное устройство соперничает с прецизионным обнаружителем, использующим алгоритм быстрого преобразования Фурье, и обладает возможностями, которые могут превосходить возможности обычных анализаторов спектра, когда неизвестный синусоидальный сигнал имеет конечную полосу частот или является модулированным по частоте. Этот способ иллюстрируется схемой на рис. 19.11.

Здесь входной сигнал представляет собой сумму синусоидального сигнала и шума. На выходе системы формируется дискретное преобразование Фурье (ДПФ) от импульсной характеристики фильтра. Сигнал обнаруживается тогда, когда спектральный пик превышает фоновый шум.

Отметим, что в схеме на рис. 19.11., кроме того, имеется выходной сигнал фильтра y, который можно использовать непосредственно или в качестве входного сигнала анализатора спектра или устройства фазовой автоподстройки. Более того, способ, иллюстрируемый на рис. 19.11., можно применять при одновременном обнаружении множества синусоидальных сигналов.

На входе действует белый шум с общей мощностью v², а входной сигнал имеет на нормированной частоте ω₀ мощность С²/2. Идеальная импульсная характеристика, эквивалентная отклику согласованного фильтра, представляет собой отсчеты синусоиды, имеющей частоту ω₀. Общий сдвиг фазы отклика на частоте ω₀ и задержки кратен 360°. Если значение пика передаточной функции равно а, то значение пика весовых коэффициентов составляет примерно 2a/(L+1), где L+1 – число весовых коэффициентов.

В результате адаптивного процесса минимизируется среднеквадратическая ошибка E[ε_k²]. В рассматриваемом случае она является суммой трех составляющих: мощности шума на входе, мощности шума на выходе адаптивного фильтра и мощности синусоидального сигнала, т.е. СКО можно записать в виде

. (19.28)

В этом выражении v² – мощность шума на входе, во втором слагаемом v² умножено на сумму квадратов весовых коэффициентов фильтра, а третье слагаемое представляет собой разность мощностей входного и отфильтрованного синусоидального сигналов; при этом полагаем, что сигналы вычитаются когерентно.

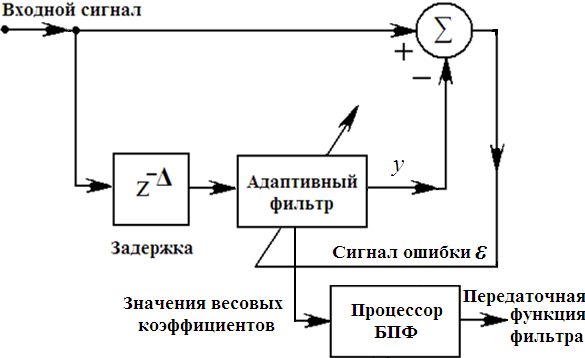
Рис. 19.11. Схема адаптивного накопителя

Приравнивая нулю производную выражения (19.14) по а, получаем оптимальное значение а*, при котором минимальная мощность сигнала ошибки:

. (19.15)

При больших значениях сигнал-шум а* близко к 1, при малых – меньше 1. Для того чтобы а* приближалось к 1 при малых отношениях сигнал-шум, можно использовать большое число адаптивных весовых коэффициентов.

На рисунке 19.12. для сравнения приведены некоторые экспериментальные результаты моделирования на ЭВМ процесса измерения спектральной плотности мощности с помощью ДПФ и с применением адаптивного накопителя. В каждом из трех случаев одни и те же данные анализируются методом ДПФ, а затем подаются на адаптивный накопитель.

Рис. 19.12. Классический спектральный анализ (ДПФ) – слева и адаптивное накопление – справа:

а – одночастотный сигнал в белом шуме; б – одночастотный сигнал в смеси из белого (50%) и окрашенного (50%) шумов; в – одночастотный сигнал с другой частотой в смеси белого (50%) и окрашенного (50%) шумов

Анализ всех кривых, приведенных на рисунке 19.12. в одном и том же масштабе, показывает, что амплитуды составляющих сигнала приблизительно одинаковы и, кроме того, аналогичны уровни фонового шума как для алгоритма ДПФ, так и для накопителя. В каждом случае накопитель реализуется с задержкой в 256 отсчетов, выбранной так, чтобы составляющие окрашенного шума были некоррелированными и подавлялись.

Очевидно, что адаптивный накопитель можно применять в качестве альтернативы к алгоритму ДПФ при обнаружении и оценке слабых сигналов на фоне шума. Кроме того, его можно использовать в качестве следящего фильтра, который автоматически настраивается на сигналы или отстраивается от них. При этом реализуется методология спектрального анализа, связанная с методом максимальной энтропии. По своей структуре накопитель полностью отличен от устройства вычисления ДПФ, и в некоторых случаях его легче реализовать.

Адаптивное подавление помех представляет собой способ оптимальной фильтрации, который можно применять всегда, когда имеется подходящий эталонный входной сигнал. Принципиальными достоинствами этого способа являются его адаптивность, низкий уровень помех на выходе и малые вносимые искажения сигнала. Адаптивность позволяет обрабатывать входные сигналы с неизвестными свойствами и в некоторых случаях нестационарные сигналы. Этот способ приводит к устойчивой системе, которая автоматически отключается, если не достигается улучшения отношения сигнал-шум. В общем случае уровень помех на выходе и степень искажения сигнала ниже достигаемых в обычных схемах оптимальных фильтров.