17.7. Потенциальная помехоустойчивость некогерентного приёма

Определим потенциальную помехоустойчивость некогерентного приема на примере системы с пассивной паузой при равных априорных вероятностях посылок

s₁(t) = A cos(ωt + φ), s₀(t) = 0, p₁ = p₀ = 0,5.

Средняя вероятность ошибки равна

.

Здесь w₁(V|H₁) и w₀(V|H₀) – условные плотности распределения вероятности огибающей корреляционного интеграла при условии гипотез о передаче сигналов s₁(t) и s₀(t) соответственно, V_п – порог (рис. 17.10).

При гипотезе H₀ значение огибающей обусловлено только шумом, тогда квадратурные составляющие являются независимыми нормальными случайными величинами с нулевыми средними и дисперсиями N₀E/2 (см. выражение 4.17).

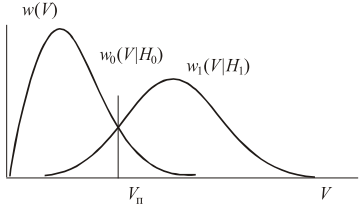
Рис. 17.10. Выбор порога при некогерентном приеме

Условная плотность распределения вероятностей огибающей имеет рэлеевский вид

.

Если наблюдаемое колебание содержит сигнал s₁(t), то огибающая имеет обобщенное рэлеевское распределение (распределение Рэлея – Райса)

.

Средняя вероятность ошибки равна

. (17.20)

Второй интеграл берется по частям, при этом

.

Оптимальное значение порога, при котором достигается потенциальная помехоустойчивость некогерентного приема, является решением уравнения dp_ош/dV_п = 0. Точно решить полученное уравнение не удается. Поэтому оптимальный порог определяется приближенными выражениями

Подставляя в (4.20) порог E/2, получим среднюю вероятность ошибки при больших отношениях сигнал/шум (ОСШ):

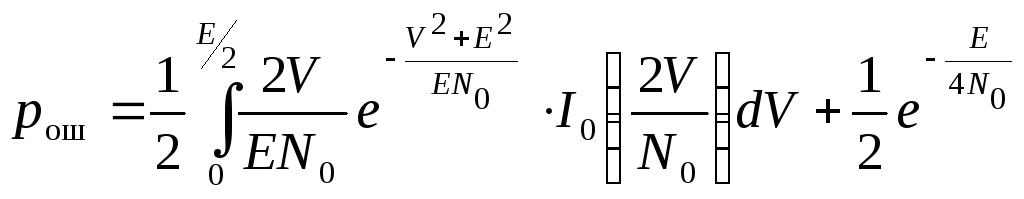
При больших ОСШ (E/N₀ ≥ 10) первым слагаемым можно пренебречь, тогда

.

Аналогично можно проанализировать помехоустойчивость приема двух ортогональных частотно-манипулированных сигналов; для этого случая средняя вероятность ошибки

.

Сигналы с фазовой манипуляцией при случайной начальной фазе каждой посылки, очевидно, применять при некогерентном приеме нельзя. Однако при медленных изменениях фазы можно использовать относительную фазовую манипуляцию, при которой начальная фаза следующей посылки совпадает с начальной фазой предыдущей посылки при передаче символа «0» и отличается от нее на 180⁰ – при передаче символа «1». При этом средняя вероятность ошибки

.

18. Помехоустойчивость систем передачи непрерывных сообщений

Непрерывные сообщения (например, речь, музыка и т.п.) могут передаваться по каналу связи непосредственно (например, по местной проводной радиосети, по телефонному кабелю) или при помощи модуляции. В первом случае сигнал s(t), передаваемый по каналу, может совпадать с сообщением (первичным сигналом) b(t) или быть связан с ним простой пропорциональной зависимостью, во втором – передаваемый сигнал s[t, b(t)] является функцией сообщения, в общем случае нелинейной (рис. 18.1).

Рис. 18.1. Структура системы передачи непрерывных сообщений

Колебание на входе демодулятора z(t) = s[t, b(t)] + ξ(t) представляет собой в простейшем случае сумму передаваемого сигнала и шума ξ(t).

Задача демодулятора состоит в нахождении оценки первичного сигнала (сообщения), наилучшую в смысле выбранного критерия близости. В качестве критерия часто используют средний квадрат ошибки

, (18.1)

где черта означает статистическое усреднение по ансамблю. В системах телеметрии используется критерий максимальной ошибки, в радиовещании – увеличение выходного отношения сигнал/шум по сравнению с входным, критерий разборчивости речевых сообщений и т.п.