
- •Теория электрической связи
- •Оглавление
- •I. Сообщения, сигналы и помехи, их математические модели
- •1. Общие сведения о системах электрической связи
- •1.1. Информация, сообщения, сигналы и помехи
- •1.2. Общие принципы построения систем связи
- •1.3. Классификация систем связи
- •2. Математическая модель сигналов
- •2.1. Математическое описание сигнала
- •2.2. Математическое представление сигналов
- •2.3. Геометрическое представление сигналов
- •2.4. Представление сигналов в виде рядов ортогональных функций
- •3. Спектральные характеристики сигналов
- •3.1. Спектральное представление периодических сигналов
- •3.2. Спектральное представление непериодических сигналов
- •3.3. Основные свойства преобразования Фурье:
- •1) Линейность.
- •4) Теорема запаздывания.
- •10) Спектры мощности.
- •4. Сигналы с ограниченным спектром. Теорема Котельникова
- •4.1. Разложение непрерывных сигналов в ряд Котельникова
- •Спектр периодической последовательности дельта-импульсов в соответствии с формулой для u(t) имеет следующий вид:
- •4.2. Спектр дискретизированного сигнала
- •4.3. Спектр дискретизированного сигнала при дискретизации импульсами конечной длительности (сигнал амплитудно-импульсной модуляции или аим сигнал)
- •4.4. Восстановление непрерывного сигнала из отсчётов
- •4.5. Погрешности дискретизации и восстановления непрерывных сигналов
- •5. Случайные процессы
- •5.1. Характеристики случайных процессов
- •Функция распределения вероятностей сп (фрв).
- •Двумерная фрв.
- •Функция плотности вероятностей случайного процесса (фпв)
- •Стационарность.
- •Эргодичность.
- •5.2. Нормальный случайный процесс (гауссов процесс)
- •5.3. Фпв и фрв для гармонического колебания со случайной начальной фазой
- •5.4. Фпв для суммы нормального случайного процесса и гармонического колебания со случайной начальной фазой
- •5.5. Огибающая и фаза узкополосного случайного процесса
- •5.6. Флуктуационный шум
- •6. Комплексное представление сигналов и помех
- •6.1. Понятие аналитического сигнала
- •6.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- •7. Корреляционная функция детерминированных сигналов
- •7.1. Автокорреляция вещественного сигнала
- •Свойства автокорреляционной функции вещественного сигнала:
- •7.2. Автокорреляция дискретного сигнала
- •7.3. Связь корреляционной функции с энергетическим спектром
- •7.4. Практическое применение корреляционной функции
- •II. Методы формирования и преобразования сигналов
- •8. Модуляция сигналов
- •8.1. Общие положения
- •8.2. Амплитудная модуляция гармонического колебания
- •8.3. Балансная и однополосная модуляция гармонической несущей
- •9. Методы угловой модуляции
- •9.1. Принципы частотной и фазовой (угловой) модуляции
- •9.2. Спектр сигналов угловой модуляции
- •9.3. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- •9.4. Формирование и детектирование сигналов угловой модуляции
- •10. Манипуляция сигналов
- •10.1. Временные и спектральные характеристики амплитудно- манипулированных сигналов
- •10.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- •10.3. Фазовая (относительно-фазовая) манипуляция сигналов
- •III. Алгоритмы цифровой обработки сигналов
- •11. Основы цифровой обработки сигналов
- •11.1. Общие понятия о цифровой обработке
- •11.2. Квантование сигнала
- •11.3. Кодирование сигнала
- •11.4. Декодирование сигнала
- •12. Обработка дискретных сигналов
- •12.1. Алгоритмы дискретного и быстрого преобразований Фурье
- •12.2. Стационарные линейные дискретные цепи
- •12.3. Цепи с конечной импульсной характеристикой (ких-цепи)
- •12.4. Рекурсивные цепи
- •12.5. Устойчивость лис-цепей
- •13. Цифровые фильтры
- •13.1. Методы синтеза ких-фильтров
- •13.2. Синтез бих-фильтров на основе аналого-цифровой трансформации
- •IV. Каналы связи
- •14. Каналы связи
- •14.1. Модели непрерывных каналов
- •14.2. Модели дискретных каналов
- •V. Теория передачи и кодирования сообщений
- •15. Теория передачи информации
- •15.1. Количество информации переданной по дискретному каналу
- •15.2. Пропускная способность дискретного канала
- •15.3. Пропускная способность симметричного дискретного канала без памяти
- •15.4. Методы сжатия дискретных сообщений
- •15.4.1. Условия существования оптимального неравномерного кода
- •15.4.2. Показатели эффективности сжатия
- •15.4.3. Кодирование источника дискретных сообщений методом Шеннона-Фано
- •15.4.4. Кодирование источника дискретных сообщений методом Хаффмена
- •15.5. Количество информации, переданной по непрерывному каналу
- •15.6. Пропускная способность непрерывного канала
- •16. Теория кодирования сообщений
- •Классификация помехоустойчивых кодов
- •16.1. Коды с обнаружением ошибок
- •16.1.1. Код с проверкой на четность.
- •16.1.2. Код с постоянным весом.
- •16.1.3. Корреляционный код (Код с удвоением).
- •16.1.4. Инверсный код.
- •16.2. Корректирующие коды
- •16.2.1. Код Хэмминга
- •16.2.2. Циклические коды
- •16.2.3. Коды Рида-Соломона
- •V. Помехоустойчивость
- •17. Помехоустойчивость систем передачи дискретных сообщений
- •17.1. Основные понятия и термины
- •17.2. Бинарная задача проверки простых гипотез
- •17.3. Приём полностью известного сигнала (когерентный приём)
- •17.4. Согласованная фильтрация
- •17.5. Потенциальная помехоустойчивость когерентного приёма
- •17.6. Некогерентный приём
- •17.7. Потенциальная помехоустойчивость некогерентного приёма
- •18. Помехоустойчивость систем передачи непрерывных сообщений
- •18.1. Оптимальное оценивание сигнала
- •18.2. Оптимальная фильтрация случайного сигнала
- •18.3. Потенциальной помехоустойчивости передачи непрерывных сообщений
- •19. Адаптивные устройства подавления помех
- •19.1. Основы адаптивного подавления помех
- •19.2. Подавление стационарных помех
- •19.3. Адаптивный режекторный фильтр
- •19.4. Адаптивный высокочастотный фильтр
- •19.5. Подавление периодической помехи с помощью адаптивного устройства предсказания
- •19.6. Адаптивный следящий фильтр
- •19.7. Адаптивный накопитель
- •VI. Многоканальная связь и распределение информации
- •20. Многоканальная связь и распределение информации
- •20.1. Частотное разделение каналов
- •20.2. Временное разделение каналов
- •20.3. Кодовое разделение каналов
- •20.4. Синхронизация в спи с многостанционным доступом
- •20.5. Коммутация в сетях связи
- •VII. Эффективность систем связи
- •21. Оценка эффективности и оптимизация параметров телекоммуникационных систем (ткс)
- •21.1. Критерии эффективности
- •21.2. Эффективность аналоговых и цифровых систем
- •21.3. Выбор сигналов и помехоустойчивых кодов
- •22. Оценка эффективности радиотехнической системы связи
- •22. 1. Тактико-технические параметры радиотехнической системы связи
- •22.2. Оценка отношения сигнал/помеха на входе радиоприемники радиотехнической системы связи
- •22.3. Оптимальная фильтрация непрерывных сигналов
- •22.4. Количество информации при приёме дискретных сигналов радиотехнической системы связи
- •22.5. Количество информации при оптимальном приёме непрерывных сигналов
- •22.6. Выигрыш в отношении сигнал/помеха
- •22.7. Пропускная способность каналов радиотехнической системы связи
- •VIII. Теоретико-информационная концепция криптозащиты сообщений в телекоммуникационных системах
- •23. Основы криптозащиты сообщений в системах связи
- •23.1. Основные понятия криптографии
- •23.2. Метод замены
- •23.3. Методы шифрования на основе датчика псевдослучайных чисел
- •23.4. Методы перемешивания
- •23.5. Криптосистемы с открытым ключом
- •13.6. Цифровая подпись
- •Заключение
- •Список сокращений
- •Основные обозначения
- •Литература
- •Теория электрической связи
10) Спектры мощности.
Временная функция мощности сигнала в общей форме определяется выражением:
w(t) = s(t) s*(t) = |s(t)|2.
Спектральная плотность мощности, соответственно, равна преобразованию Фурье произведения s(t)·s*(t), которое отобразится в спектральном представлении сверткой Фурье-образов этих функций:
![]() (3.15)
(3.15)
Но для всех текущих значений частоты f интеграл в правой части этого выражения равен произведению S(f)·S*(f), так как для всех значений сдвига v ≠ 0 в силу ортогональности гармоник S(f) и S*(f - v) значения их произведения равны нулю. Отсюда:
W(f) = S(f) * S*(f) = |S(f)|2. (3.16)
Спектр мощности – вещественная неотрицательная четная функция, которую очень часто называют энергетическим спектром. Спектр мощности, как квадрат модуля спектра сигнала, не содержит фазовой информации о частотных составляющих, а, следовательно, восстановление сигнала по спектру мощности невозможно. Это означает также, что сигналы с различными фазовыми характеристиками могут иметь одинаковые спектры мощности. В частности, сдвиг сигнала не отражается на его спектре мощности.
Для функций мощности взаимодействия сигналов в частотной области соответственно имеем частотные спектры мощности взаимодействия сигналов:
Wxy(f) = X(f) Y*(f),
Wyx(f) = Y(f) X*(f),
Wxy(f) = W*yx(f).
Функции мощности взаимодействия сигналов комплексные, даже если обе функции x(t) и y(t) вещественны, при этом Re[Wxy(f)] – четная функция, а Im[Wxy(f)] – нечетная. Отсюда полная энергия взаимодействия сигналов при интегрировании функций мощности взаимодействия определяется только реальной частью спектра:
![]()
и всегда является вещественным числом.
11) Равенство Парсеваля. Полная энергия спектра сигнала:
![]() (3.17)
(3.17)
Так как координатное и частотное представление по существу только разные математические отображения одного и того же сигнала, то равной должна быть и энергия сигнала в двух представлениях, откуда следует равенство Парсеваля:
![]()
т.е. энергия сигнала равна интегралу модуля его частотного спектра – сумме энергий всех частотных составляющих сигнала. Аналогично для энергии взаимодействия сигналов:
![]()
Из равенства Парсеваля следует инвариантность скалярного произведения сигналов и нормы относительно преобразования Фурье:
(x(t),y(t)) = (X(f),Y(f)), ||x(t)||2 = ||X(f)||2.
Не следует забывать, что при представлении спектров в круговых частотах (по ω) в правой части приведенных равенств должен стоять множитель 1/2π.
4. Сигналы с ограниченным спектром. Теорема Котельникова
4.1. Разложение непрерывных сигналов в ряд Котельникова
Как отмечено ранее, любые сигналы конечной длительности теоретически имеют бесконечно широкий спектр частот. В то же время доля энергии, передаваемая на высоких частотах, очень мала и ею при расчете полной энергии сигнала можно пренебречь. Следовательно, сигналы с ограниченным спектром являются удобными математическими моделями реальных сигналов.
В 1933 году В. А. Котельников доказал, что сигнал х(t) с ограниченной полосой частот, не имеющий спектральных компонент с частотами, которые превышают значение ωв = 2πFв, однозначно определяется значениями, выбранными через равные промежутки времени [1]
Δt = π/ωв = 1/2Fв.

Рис. 4.1. Временные диаграммы непрерывного сигнала s(t) и дискретизированного sд(t)
Важно, что не надо передавать непрерывно исходный сигнал s(t), достаточно передавать отсчёты s(kt). Это первый шаг перехода от непрерывного сигнала к цифровому. С точки зрения математики теорема Котельникова означает представление сигнала в виде ряда:
![]() (4.1)
(4.1)
![]()
Ряд Котельникова – это разложение сигнала s(t) в ряд по ортогональным функциям φk(t).
![]() (4.2)
(4.2)
Теоретически дискретизация осуществляется с помощью -импульсов.
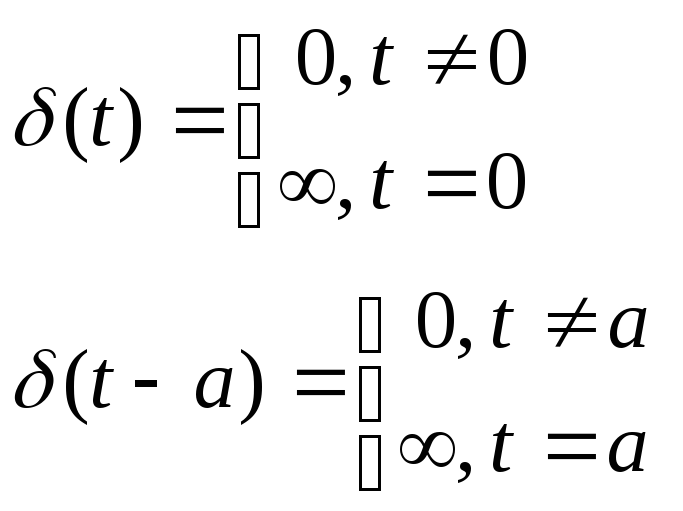

Рис. 4.2. Временная диаграмма одиночного -импульса
Спектр одиночного -импульса получим, используя преобразование Фурье:
![]()
Использовано "фильтрующее" свойство дельта-функций:
![]()
Следовательно, спектр одиночного дельта-импульса имеет вид:

Рис. 4.3. Спектр одиночного δ-импульса
Чтобы получить отсчёты функции s(t) перемножим функцию s(t) на периодическую последовательность дельта-импульсов с периодом Т = t.
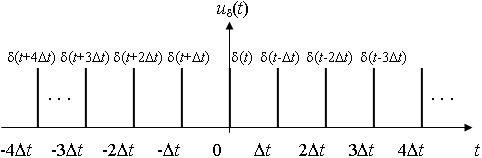
Рис. 4.4. Временная диаграмма периодической последовательности
δ-импульсов
Так как сигнал периодический, то его спектр будет дискретным.
![]() (4.3)
(4.3)
 ;
;
![]()
Т = t; ωд – частота дискретизации.
