
Algebra
.pdfx = x1a1 +x2a2 + +xnan ,
что и доказывает теорему.
Коэффициенты x1, x2,…, xn разложения вектора x по векторам базиса a1, a2, …, an называются координатами вектора x в данном базисе. В силу един ственности линейного выражения вектора через линейно независимые векторы, как было доказано ранее, координаты вектора в данном базисе определяются однозначно. Координаты вектора, определенные при введении понятия вектора,
— это коэффициенты разложения данного вектора по единичному базису. Пусть дана прямоугольная матрица
a11 |
a12 |
a1n |
|
|
a |
a |
a |
|
m×n . |
A = 21 |
22 |
2n |
||
|
|
|
|
|
am1 |
am2 |
amn |
|
|
Можно доказать, что ранг системы строк
(a11 a12 |
a1n ), (a21 |
a22 |
|
a2n ),…, (am1 am2 |
amn ) |
||||
произвольной матрицы A равен рангу системы ее столбцов |
|
||||||||
|
a11 |
|
|
a12 |
|
|
a1n |
|
|
|
a |
|
, |
a |
|
,…, |
a |
|
|
|
21 |
|
22 |
|
2n . |
|
|||
|
|
|
|
|
|
|
|
|
|
|
am1 |
|
am2 |
|
amn |
|
|||
Данный результат позволяет ввести новое понятие: рангом матрицы на зывается максимальное число ее линейно независимых параллельных рядов. Обозначается ранг матрицы A так: rg A. Очевидно, что если A m×n , то rg A -min{m, n}
Под элементарными преобразованиями матрицы будем понимать преоб разования трех типов:
•перемена местами двух каких нибудь строк;
•умножение всех элементов одной из строк матрицы на число, отличное от нуля;
•прибавление ко всем элементам одной из строк матрицы соответствующих элементов другой строки, умноженных на одно и то же число.
Несложно доказать такую теорему.
ТЕОРЕМА 2.2.10. Элементарные преобразования матрицы не изменяют ее ранга.
Эта теорема дает способ вычисления ранга матрицы: с помощью элемен тарных преобразований матрицу приводят (с точностью до перестановки столбцов) к виду
41
|
1 |
0 |
0 |
|
|
|
|
|
||
|
|
0 |
1 |
0 |
|
|
|
|
|
|
r строк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
, |
(2.2.4) |
||||
|
0 |
0 |
0 |
0 |
0 |
0 |
||||
|
|
|
||||||||
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
0 |
0 |
|
|
||||||
где звездочками обозначены произвольные числа, при этом ранг исходной матрицы равен рангу преобразованной матрицы, а ранг преобразованной мат рицы, очевидно, равен r.
2.2.1. Найти базис и ранг системы векторов — строк матрицы
|
0 |
1 |
2 |
|
|
|
|
|
|
A = |
4 |
0 |
1 |
. |
|
|
−1 |
1 |
|
3 |
|
|||
из примера 1.3.1.
Решение. Преобразуем матрицу A с помощью элементарных преобразований. Процесс элементарных преобразований иллюстрируется табл. 2.2.1.
Т а б л и ц а 2.2.1
|
A |
|
Примечания |
0 |
1 |
2 |
II → I |
4 |
0 |
1 |
I → II |
3 |
–1 |
1 |
III → III |
4 |
0 |
1 |
(1/4) I → I |
0 |
1 |
2 |
II → II |
3 |
–1 |
1 |
III → III |
1 |
0 |
1/4 |
I → I |
0 |
1 |
2 |
II → II |
3 |
–1 |
1 |
III – 3 I → III |
1 |
0 |
1/4 |
I → I |
0 |
1 |
2 |
II → II |
0 |
–1 |
1/4 |
III + II → III |
1 |
0 |
1/4 |
I –(1/9) III → I |
0 |
1 |
2 |
II –(8/9) III → II |
0 |
0 |
9/4 |
(4/9) III → III |
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
|
Таким образом, исходная матрица
0 |
1 |
2 |
|
|
|
4 |
0 |
1 |
|
A = |
. |
|||
|
|
−1 |
1 |
|
3 |
|
|||
с помощью элементарных преобразований приведена к виду
42
1 |
0 |
0 |
|
|
|
|
0 |
1 |
0 |
|
, |
|
|
||||
|
|
0 |
1 |
|
|
0 |
|
|
|||
откуда следует что три строки матрицы A:
( |
0 |
1 2 |
) |
, |
( |
4 |
) |
( |
3 |
) |
(2.2.5) |
|
|
|
0 1 , |
|
−1 1 |
представляют собой линейно независимую систему векторов.
Эти три вектора (2.2.5) и образуют базис системы векторов — строк матрицы A. Ранг системы векторов равен числу векторов в базисе этой системы, т. е., в данном случае, трем.
ПРИМЕР 2.2.2. Определить ранг матрицы А из примера 2.2.1.
Решение. Ранг матрицы равен рангу системы векторов — строк этой матрицы, т. е., согласно решению примера 2.2.1, rg A =3 .
В о п р о с ы д л я с а м о п р о в е р к и
1.Какие векторы называются линейно зависимыми?
2.Какие векторы называются линейно независимыми?
3.Сформулируйте необходимое и достаточное условие линейной зависи мости векторов линейного пространства.
4.Что такое базис линейного пространства?
5.Что такое размерность линейного пространства?
6.Как связаны между собой размерность линейного пространства и число элементов в базисе этого пространства?
7.Что такое координаты элемента линейного пространства в данном базисе?
8.Может ли базис линейного пространства содержать нулевой элемент этого пространства?
9.Верно ли, что произвольный вектор линейного пространства может быть разложен по базису a1, a2, …, an этого пространства?
10.Являются ли элементы a1, a2, …, an линейно независимыми, если извест но, что некоторый элемент x можно представить в виде двух различных ли нейных комбинаций элементов a1, a2, …, an?
11.Верно ли, что элементы c1a1, c2a2, …, cnan (где c1, c2, …, cn — числа, не рав ные нулю) образуют базис линейного пространства, если известно, что a1, a2, …, an — базис этого пространства?
12.Сколько различных базисов существует в n мерном линейном про странстве?
13.Может ли размерность линейного пространства быть меньше размерно сти его подпространства?
14.Верно ли, что ранг системы векторов — строк матрицы равен рангу сис темы векторов — столбцов этой матрицы?
15.Что такое ранг матрицы?
16.Что такое базисный минор?
17.Как изменяется ранг матрицы при ее элементарных преобразованиях?
18.Чему равен ранг единичной матрицы?
19.Чему равен ранг диагональной матрицы?
20.Чему равен ранг произведения матриц?
43
21.Как связаны rg A и rg AT?
22.Чему равен ранг квадратной невырожденной матрицы?
23.Являются ли столбцы матрицы A m×n линейно зависимыми, если rg A < n?
24.Являются ли столбцы матрицы A m×n линейно зависимыми, если rg A = n?
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
1.Даны матрицы A, B, c, d, E. Найдите rg A, rgB, rgc, rgd, rgE , если
4 |
−1 |
−3 |
|
|
2 |
8 |
|
|
3 |
|
|
|
|
2 |
−1 5 |
|
|
|
1 |
|
|
1 1 |
0 −1 |
||||
|
3 |
|
, |
|
|||||||||
A = |
0 |
|
, |
B = |
−4 |
c = |
|
, |
d =(5 2 3 1), |
E = |
. |
||
3 |
−2 |
|
|
0 |
|
|
5 |
|
2 0 |
−2 1 |
|||
0 |
7 |
1 |
|
1 |
|
−2 |
|
|
|
||||
|
|
|
|
|
|
|
|||||||
2.Найдите rg A, rgB, rgC, rgD , если
2 5 |
|
2 |
8 |
3 |
2 |
−2 |
|
5 |
0 |
0 |
|||
|
|
|
|
|
|
|
|
|
|
||||
A = |
, |
B = |
, |
C = |
4 |
1 |
0 |
, |
D = |
0 |
5 |
0 |
. |
1 0 |
|
3 |
−4 |
|
−1 5 |
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
2 |
|
5 |
||||||
§ 2.3. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА ЛИНЕЙНЫХ ПРОСТРАНСТВ
Прямая линия с заданным на ней направлением называется осью. Если вы брать на оси некоторую точку O, называемую началом координат, и задать е д и н и ц у и з м е р е н и я (масштаба), то тем самым мы зададим систему координат на прямой.
Две перпендикулярные оси на плоскости с общим началом координат и одина ковой единицей измерения образуют декартову прямоугольную систему коор динат на плоскости. Одна из осей называется осью абсцисс и обозначается Oх1, другая — осью ординат (Ox2), а сама система координат обозначается х1Ox2.
Аналогичным образом можно ввести декартову прямоугольную систему ко ординат и в трехмерном пространстве.
Проекции точки на координатные оси называются координатами этой точ ки. Очевидно, любая точка однозначно задается своими координатами.
С произвольной точкой M однозначным образом связан так называемый ра диус вектор этой точки, т. е. вектор, имеющий те же координаты, что и точка
M. С геометрической точки зрения радиус вектор точки M — это вектор OM , началом которого является начало координат O, а концом — данная точка M.
На рис. 2.3.1 изображена декартова прямоугольная система координат на плоскости. В этой системе координат отмечены точки A(1, 4), B(2, 3), C(–1, 2) и D(–1, –1). С этими точками связаны их радиус векторы a = (1, 4), b = (2, 3), c = (–1, 2) и d = (–1, –1).
44

x2
b
a + b
A
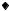 B
B
C a
a
c 1 |
b |
|
x1 |
||
|
D d O 1
d O 1
4d
Рис. 2.3.1. Декартова прямоугольная система координат на плоскости
Теперь операции над векторами получают наглядную геометрическую ин
терпретацию.
Для того, чтобы получить сумму векторов a и b, нужно вектор b отложить из конца вектора a и в качестве результата a + b взять вектор с началом в начале вектора a и с концом в конце вектора b.
Чтобы получить вектор λa , нужно построить вектор, который имеет то же направление, что и вектор a, если λ.0 , или противоположное направление, если λ <0 , а длину — в λ раз больше, чем длина вектора a.
Построим на рис. 2.3.1, пользуясь этими правилами, векторы a + b и 4d.
Их координаты a +b =(3, 7), 4d =(−4, −4) совпадают с вычисленными по обыч ным формулам сложения векторов и умножения вектора на число из § 1.1:
a +b =(3, 7) =(1+2, 4 +3), 4d =(−4, −4) =(−1 4, −1 4) .
Аналогии между линейными пространствами произвольной природы и при вычными нам прямой линией, плоскостью и обычным трехмерным простран ством позволяют пойти дальше: ввести понятия длины вектора, угла между векторами и расстояния между точками в произвольном линейном простран стве.
Длиной вектора a =(a1, a2,…, an )
n
| a | = a12 +a22 + +an2 = ∑ai2 = a, a ,
i=1
ТЕОРЕМА 2.3.1 (НЕРАВЕНСТВО КОШИ — БУНЯКОВСКОГО). Скалярное произведение
произвольных векторов a и b не превосходит произведения их длин: |
|
a, b -| a | | b | . |
(2.3.1) |
|
45 |

Доказательство. Если a = 0, то a, b =0, | a | =| b| =0 , откуда и следует неравенство
(2.3.1), превращающееся в этом случае в равенство. |
Пусть теперь a ≠ 0 и пусть |
|
x = αa −b , где α |
— некоторое число. Тогда по свойству скалярного произведения |
|
x, x .0 [см. формулу (1.1.12)] или |
|
|
x, x = αa −b, αa −b = α a, αa −b − b, αa −b = α2 a, a −α a, b −α b, a + b, b = |
||
|
= α2 a, a −2α a, b + b, b , |
|
т. е. при любом α |
выполняется неравенство |
|
|
α2 a, a −2α a, b + b, b .0 , |
|
Так как a ≠ θ, то |
a, a ≠0 и можно положить α = a, b |
: |
|
a, a |
|
a, b
a, a
2 |
|
a, b |
|
2 |
a, a −2 |
a, b + b, b .0 , |
|
|
|
a, a |
|
откуда |
|
|
|
|
|
a, b 2 |
−2 |
a, b 2 |
+ b, b .0 или |
a, b 2 |
- b, b . |
a, a |
|
a, a |
|
a, a |
|
Умножив левую и правую части последнего неравенства на одно и то же число
a, a >0 , получим: |
|
a, b 2 - a, a b, b , |
(2.3.2) |
и чтобы теперь получить неравенство (2.3.1), достаточно взять квадратный корень из обеих (неотрицательных) частей неравенства (2.3.2) и вспомнить, что | a | = a, a ,
| b| = b, b . Теорема доказана.
Поскольку из теоремы 2.3.1 следует, что если оба вектора a и b ненулевые, то
−1- a, b -1, |
(2.3.3) |
|a | | b |
иможно определить угол ϕ=(a, b) между ненулевыми векторами a и b как та
кое число ϕ=[0, π] , что
cos ϕ=cos(a, b) = a, b . | a | | b |
Читателю рекомендуется убедиться в справедливости неравенства (2.3.3).
ПРИМЕР 2.3.1. Определить угол между векторами a =( 3, 3), b =(−1, 3 ).
Решение. Вычисляем последовательно:
a, b = 3(−1) +3 3 =2 3, | a |= a, a = ( 3 )2 +32 = 12 =2 3,
46

| b |= b, b = (−1)2 +( 3 )2 = 4 =2, cos(a, b) = a, b |
= |
2 3 |
= |
1 |
, |
2 3 2 |
|
||||
| a | | b | |
|
2 |
|
||
откуда (a, b) = π/3 =60 . Рис. 2.3.2 подтверждает это наглядно.
|
|
x2 |
|
|
1 |
π |
a |
b |
|
||
3 |
x1 |
||
|
|
|
|
|
|
O 1 |
|
Рис. 2.3.2. Угол между векторами
Два вектора пространства называются ортогональными, если их скалярное произведение равно нулю. С геометрической точки зрения ортогональные векторы перпендикулярны друг другу.
Расстояние между точками A(a1, a2,…, an ) и B(b1, b2,…, bn ) равно, очевидно, длине вектора AB =(b1 −a1, b2 −a2,…, bn −an ) :
n
ρ(A, B) = (b1 −a1 )2 +(b2 −a2 )2 + +(bn −an )2 = ∑(bi −ai )2 = b −a, b −a .
i=1
В о п р о с ы д л я с а м о п р о в е р к и
1.Что такое прямоугольная декартова система координат?
2.Каким аксиомам должно удовлетворять скалярное произведение векто ров линейного пространства?
3.Как формулируется неравенство Коши — Буняковского?
4.Что такое евклидово пространство?
5.Как в евклидовом пространстве определяется длина вектора?
6.Как в евклидовом пространстве определяется расстояние между двумя векторами?
7.Как в евклидовом пространстве определяется угол между двумя векто рами?
8.Какие векторы называются ортогональными?
9.Всякая ли ортогональная система векторов является линейно независи
мой?
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
1.Проверьте, являются ли векторы a = (10, 10, 0) и b = (–1, –1, 2) ортого нальными, и если не являются, найти косинус угла между этими векторами.
2.Найдите расстояние между точками A(10, 0, 0) и B(–20, –40, 0).
47
Глава 3. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
ИНЕРАВЕНСТВ
§3.1. ОПРЕДЕЛЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Вэкономических исследованиях, планировании и управлении приходится рассматривать системы алгебраических уравнений со многими неизвестными величинами. Система из k уравнений первой степени с n неизвестными мо жет быть записана в виде
a11x1 |
+ a12x2 |
+ |
+ a1nxn |
||||||
a x |
+ a x |
+ |
+ a |
|
x |
n |
|||
|
21 |
1 |
22 |
2 |
|
2n |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ a |
|
+ |
+ a |
|
|
|
a |
x |
x |
x |
|
|||||
|
k1 |
1 |
k2 |
2 |
|
kn |
|
n |
|
= b1,
= b2,
(3.1.1)
= bk ,
где н е и з в е с т н ы е |
x1, x2,…, xn подлежат определению, а к о э ф ф и ц и |
е н т ы a11,a12,…,akn |
п р и н е и з в е с т н ы х и с в о б о д н ы е ч л е н ы |
b1,b2,…,bk у р а в н е н и й заданы, притом первый индекс коэффициента сов падает с номером уравнения, в котором содержится данный коэффициент, второй индекс — с номером неизвестной, при которой этот коэффициент по ставлен. Кратко запишем систему линейных алгебраических уравнений в сле дующем виде:
n
∑aijxj =bi , i =1,2,…,k .
j=1
Совокупность чисел α1,α2,…,αn , взятых в определенном порядке, называют решением системы уравнений (7.2.1), если они, будучи подставлены в уравне ния системы на место соответствующих неизвестных, обращают все уравне ния в тождества. Решение (α1,α2,…,αn ) системы (3.1.1) называют неотрица тельным, если все его компоненты αi неотрицательны.
Система линейных алгебраических уравнений (3.1.1) называется совмест ной, если она имеет решение. Совместная система называется определенной или неопределенной в зависимости от того, имеет ли она одно или более реше ний. Система вида (3.1.1) называется несовместной или противоречивой, если она не имеет решения.
Две системы линейных алгебраических уравнений с одним и тем же числом неизвестных называются эквивалентными, или равносильными, если они или обе несовместны, или обе совместны и имеют одни и те же решения; число уравнений в эквивалентных системах может быть различным. В процессе отыскания решений систему уравнений можно подвергать только таким пре образованиям, которые переводят ее в эквивалентные системы.
Относительно любой системы линейных алгебраических уравнений можно задать вопросы:
48
•совместна она или нет;
•если совместна, то каково число решений;
•как найти все решения.
Процесс отыскания ответов на первые два вопроса называется ис следованием системы, а процесс отыскания решений — решением системы.
Мы рассмотрим м е т о д Ж о р д а н а — Г а у с с а (метод последова тельного исключения неизвестных) для исследования и решения систем ли нейных алгебраических уравнений, в котором процессы исследования и поис ка решений совпадают.
Составим матрицу A из коэффициентов при неизвестных системы линей ных алгебраических уравнений. Ее принято называть матрицей системы (3.1.1), а матрицу A =(A | b) , получающуюся добавлением к A столбца свобод ных членов системы (3.1.1), называют расширенной матрицей:
a11 |
a12 |
a1n |
a11 |
a12 |
a1n |
|
a |
a |
a |
|
a |
a |
a |
A = 21 |
22 |
2n ; |
A =(A | b) = 21 |
22 |
2n |
|
|
|
|
|
|
|
|
|
ak2 |
|
|
|
ak2 |
akn |
ak1 |
akn |
ak1 |
||||
b1 b2 . bk
Очевидно, левые части уравнений системы (7.2.1) совпадают с элементами матрицы произведения Ax , поэтому систему линейных алгебраических уравнений (3.1.1) можно записать в матричной форме:
Ax =b .
ПРИМЕР 3.1.1. Проверить, является ли вектор
1 y = 202
решением системы линейных уравнений, которая задана расширенной матрицей
2 |
7 |
3 |
1 |
|
6 |
|
|
|
|
|
|||||||
|
3 |
5 |
2 |
2 |
|
4 |
|
(3.1.2) |
(A | b) = |
|
. |
||||||
|
|
|
|
|
|
|
|
|
9 |
4 |
1 |
7 |
|
2 |
|
|
|
|
|
|||||||
Решение. Подставим координаты вектора y вместо неизвестных в данную систему линейных уравнений:
2 |
1+7 2 |
+3 0 |
+1 (−2) |
=9 ≠ 6, |
|
|
+2 0 |
+2 (−2) |
=9 ≠ 4, |
3 1+5 2 |
||||
|
1+4 2 |
+1 0 |
+7 (−2) |
=1 ≠ 2. |
9 |
||||
Так как вычисленные значения не совпадают с координатами вектора b, то вектор y не является решением данной системы уравнений.
В о п р о с ы д л я с а м о п р о в е р к и
1.Что такое система линейных уравнений?
2.Что такое матрица системы линейных уравнений?
49
3.Что такое расширенная матрица системы линейных уравнений?
4.Как записать систему линейных уравнений в матричном виде?
5.Что называется решением системы линейных уравнений?
6.Какие системы линейных уравнений называются эквивалентными?
7.Какая система линейных уравнений называется совместной?
8.Какая система линейных уравнений называется определенной?
9.Верно ли, что система линейных уравнений является совместной тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной мат рицы?
10.Может ли однородная система линейных уравнений быть несовместной?
11.Верно ли, что система линейных уравнений является определенной то гда и только тогда, когда ранги матрицы системы и расширенной матрицы системы совпадают с числом неизвестных?
12.Верно ли, что система линейных уравнений с квадратной невырожден ной матрицей является совместной и определенной?
13.Что означает «исследовать систему линейных уравнений»?
14.Что означает «решить систему линейных уравнений»?
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
1. Проверьте, является ли вектор
1 x = 00
1
решением системы линейных алгебраических уравнений
4x1 −x2 +2x3 −3x4 =2, |
|||||
2x1 +3x2 |
−x3 +x4 =5, |
||||
2x |
−4x |
+3x −4x |
4 |
=3? |
|
|
1 |
2 |
3 |
|
|
2. Проверьте, является ли вектор
1 x = 0−1
6
решением системы линейных алгебраических уравнений
2x1 +x2 −3x3 −2x4 =2, |
||||
|
|
+x2 |
−2x3 |
−2x4 =2, |
3x1 |
||||
|
x |
+x |
−4x |
−3x =3? |
|
1 |
2 |
3 |
4 |
50
