Если допустить, что два электрона находятся в одном и том же состоянии, то есть Ψi = Ψk , мы получим в определителе две тождественные строки, и соответственно Ψe = 0, что удовлетво-

ряет принципу Паули.

Перестановка двух электронов местами ведет к перемене строчек местами и соответственно к изменению знака волновой функции, которая является, таким образом, антисимметричной.

Уравнение Шредингера, учитывающее потенциал Хартри и волновую функцию в виде определителя Слэтера, называется уравнением

Хартри-Фока.

Во многих случаях однако можно удовлетвориться мультип-

ликативной функцией вида ψe = ΠΨi (ri ) , помня при этом, что в системе не может быть более двух электронов с одинаковыми пространственными координатами (но отличающимися направлением спина).

2.3. Приближенные методы расчета энергетического спектра электронов в кристалле

Несмотря на значительное упрощение, которое достигнуто благодаря допущениям зонной теории, задача остается все еще очень сложной. Это связано, в первую очередь, с определением потенциальной энергии электрона U(ri,Ra) + U'(ri), входящей в одноэлектронное уравнение Шредингера.

Единственное, что можно с определенностью утверждать - это то, что данная функция - периодическая функция с периодом, равным параметру кристаллической решетки (ядра могут совершать лишь малые колебания около положения равновесия, а рас-

53

пределение электронной плотности должно соответствовать симметричному пространственному расположению ядер).

Нахождение конкретного вида этой периодической функции представляет весьма большие трудности. Не говоря уже об определении поля, создаваемого всеми ядрами в данной точ-

ке (величины U( rri , Rrα )), отметим трудности, которые возника-

ют при вычислении U'(ri).

Дело заключается в том, что в выражение для U'(ri) входит волновая функция ψj(r), которая может быть определена только в результате решения уравнения Шредингера, а для решения последнего нужно знать явный вид U'(ri).

В этой ситуации задача должна решаться методом последовательных приближений. Выбирается некоторый исходный потен-

циал U'0 и находится соответствующая ему функция ψj0 , которая затем подставляется в выражение для расчета U'(ri) , что позволяет найти следующее приближение для потенциала U'1. Эта процедура повторяется до тех пор, пока решение не оказывается самосогласованным, тo есть полученные значения U'n не совпадут (в пределах установленной точности) с предыдущим значением

U'n-1.

В зависимости от того, какой потенциал U'0 выбирается в качестве исходного, различают следующие приближения.

Приближение свободных электронов

В этом приближении потенциальная энергия электрона в поле ядер и остальных электронов считается постоянной:

54

то есть действующее на электрон поле положительно заряженных ядер полностью компенсировано полем остальных электронов.

С энергетической точки зрения кристалл в этом приближении представляет собой потенциальную яму с гладким дном. Результаты решения данной задачи известны. Движение электрона в

где к = кх ех+ ку еу+ кг ez - волновой вектор электрона, характеризующий квантовое состояние электрона в кристалле.

Показатель степени экспоненты должен быть безразмерной ве-

личиной. Поскольку rr имеет размерность длины, то волновой вектор kr должен иметь размерность, обратную длине, то есть см-1. Модуль

вой вектор пропорционален импульсу электрона. Энергия свободного

55

разность энергий между соседними уровнями настолько мала, что энергетический спектр свободных электронов можно считать квазинепрерывным.

В одномерном случае графиком зависимости Е(к) является парабола с минимумом в точке кх=0 (рис.2.2, а). В трехмерном случае (фазовом пространстве волнового вектора) зависимость Е(к) при заданной энергии представляет собой уравнение сферы

(рис.2.2, б).

Рис. 2.2. Зависимость энергии свободных электронов от волнового вектора для одномерного случая (а). Поверхность постоянной энергии в трехмерномслучае(б)

Приближение слабосвязанных электронов

В этом приближении исходят из потенциальной энергии электрона в виде

где U0 = const представляет собой потенциальную энергию электрона в поле положительных ядер, компенсированном полями остальных электронов (кроме данного), а KU(r) U0 учитывает неполную локальную компенсацию поля ядер электронами; KU(r) - периодическая функция с периодом, равным постоянной решетки.

Модель кристалла в этом приближении - трехмерная потенциальная яма со слаборифленым дном.

56

Блох доказал, что решение уравнения Шредингера в этом случае имеет вид

где ик( r ) - периодическая функция с периодом, равным постоянной решетки.

Из-за трансляционной симметрии кристалла волновые функции Ψ(r ) в точках с пространственными координатами, разли-

чающимися на вектор решетки, отличаются лишь фазовым множителем.

Таким образом, Ψ - функция в приближении слабосвязанных электронов имеет вид модулированной волны - функции Блоха. Конкретный вид этой функции определяется видом потенциальной энергии, входящей в уравнение Шредингера (т.е. KU(r)).

Если в конкретной задаче потребовать непрерывность, непрерывнодифференцируемость и периодичность волновой функции, то получаются определенные ограничения на возможные значения волнового вектора и энергии электронов.

В отличие от модели свободных электронов энергетический спектр таких (слабосвязанных) электронов приобретает зонный характер: квазинепрерывные полосы разрешенных энергий (энергетические зоны, образовавшиеся из атомных уровней) оказываются разделенными полосами запрещенных энергий.

Для простейшей модели одномерного кристалла (атомной цепочки) с параметром а зависимость энергии от волнового вектора (дисперсионное соотношение) в пределах разрешенных зон, как показывает расчет, описывается выражением вида:

где Еа - энергия атомного уровня, из которого образовалась зона; С - сдвиг атомного уровня под действием поля соседних атомов;

57

А - так называемый обменный интеграл, учитывающий возможность перехода электрона от атома к атому вследствие перекрытия волновых функций.

Чем сильнее перекрываются электронные оболочки (то есть чем с большей частотой соседние атомы обмениваются своими электронами), тем больше модуль обменного интеграла.

При этом для s-состояний А<0, а для р-состояний А>0, так что для s-зон ES(K) = E's - 2AS cos(ка)

для р-зон Ер(к) = Е'р +2АР cos(ка); где Е' = Еа + С;

As и Ар - абсолютные значения обменных интегралов для соответствующих состояний.

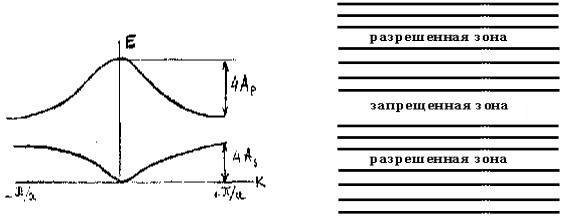
На рис.2.3. показаны графики зависимостей Е(к) для s- и р-зон. Величина Es при к=0 принимает минимальное значение,

равное E's - 2AS, a при к=±π / a достигает максимального значения E's + 2AS, так что ширина s-зоныравна4AS.

Рис.2.3. Зависимостьэнергиислабосвязанныхэлектроновотволновогочисла(а) и периодический спектр электронов(б) водномерной модели

58