
- •ВВЕДЕНИЕ
- •Вопросы и задания к главе 1
- •2. Основы зонной теории
- •2.3. Приближенные методы расчета энергетического спектра электронов в кристалле
- •2.4. Зоны Бриллюэна
- •2.5. Эффективная масса электрона
- •Вопросы и задания к главе 2
- •3. Электронные свойства полупроводников
- •3.1. Собственные и примесные полупроводники
- •3.2. Концентрация носителей заряда в собственном и слабо легированном полупроводниках
- •3.4. Поверхностные электронные состояния в полупроводниках
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
2. Основы зонной теории
Первой сравнительно удачной попыткой объяснения электрических свойств твердого тела явилась классическая теория электропроводности металлов. Она исходила из представления об образовании в металле газа свободных электронов. Однако теория свободных электронов оказалась бессильной при рассмотрении свойств твердых тел, зависящих от их внутренней структуры (так называемых структурно-чувствительных свойств).
Более того, она даже не давала ответ на такой вопрос, почему одни тела являются проводниками, а другие диэлектриками или полупроводниками; в чем причина беспрецедентного для физических свойств материалов различия их проводимости, достигающего тридцати порядков величины (от 108 Ом-1см-1 для металлов до 10-22 Ом- 1см-1 для диэлектриков при низких температурах).
Следующим этапом в развитии электронной теории твердых тел стало создание квантовой теории энергетического спектра электронов в кристалле (Ф.Блох, 1926, Л.Бриллюэн, 1930), согласно которой этот спектр состоит из чередующихся зон разрешенных и запрещенных энергий.
Изложению этой теории, получившей название зонной теории твердого тела и позволившей объяснить широкий круг явлений в кристалле, в частности различный характер электропроводности разных твердых тел, и посвящена данная глава.
43
2.1. Обобществление электроноввкристалле. Образование энергетических зон
Для понимания природы электронных свойств твердого тела рассмотрим, что происходит с электронной подсистемой, когда из одинаковых атомов образуется кристалл. Сделаем это на примере
натрия, |
атомы которого имеют электронную конфигурацию |
Is22s22p63s1 . |
|
Как видно из рисунка 2.1, а, атомы натрия, удаленные на рас- |
|
стояние, |
значительно превышающее постоянную решетки |
(г»а), разделены потенциальным барьером, препятствующим свободному переходу электронов от одного атома к другому. Электронные облака атомов не перекрываются и состояние электронов остается таким же, как и в изолированных атомах (дискретные энергетические уровни).
При образовании кристалла соседние атомы настолько сближаются друг с другом (r = а), что электронные облака, по крайней мере, внешних оболочек перекрываются (рис.2.1, б). В результате этого характер движения электронов в кристалле резко изменяется: электроны, находящиеся на определенном (достаточно высоком) энергетическом уровне одного атома, получают возможность переходить без затраты энергии на соответствующий уровень соседнего атома и таким образом свободно перемещаться вдоль всего твердого тела.
Появление возможности беспрепятственного перехода электронов от атома к атому в твердом теле связано с двумя обстоятельствами.
44
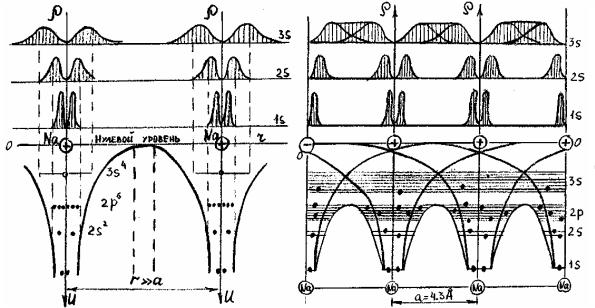
а |
б |
Рис.2.1. Энергетический спектр электронов в изолированных атомах натрия (а) и атомах натрия, сближенных на расстояния порядка параметра решетки (б)
Во-первых, при сближении атомов потенциальные кривые, характеризующие поведение электронов в изолированных атомах, частично перекрываются, что ведет к понижению потенциального барьера, разделяющего соседние атомы.
Как показано на рис.2.1, б, максимум результирующей потенциальной кривой оказывается даже ниже энергетического уровня валентных 3s-электронов атомов натрия. Перекрытие волновых функций этих электронов настолько сильно, что они дают электронное облако практически равномерной плотности.
Во-вторых, при сближении атомов уменьшается и ширина барьеров, разделяющих соседние атомы. Поэтому возникает возможность перехода электрона от атома к атому за счет туннельного эффекта.
Таким образом, в процессе образования твердого тела происходит обобществление электронов внешних оболочек атомов, причем валентные электроны обобществляются полностью, так что ве-
45
роятность обнаружения их в любом месте кристаллической решетки оказывается одинаковой.
В то же время электронные облака внутренних оболочек атомов не перекрываются, вследствие чего состояние внутренних электронов в кристалле остается практически таким же, как и в изолированных атомах (рис.2.1, б).
Иначе обстоит дело с энергетическим спектром обобществленных электронов в твердом теле. В изолированном атоме электроны, как известно, занимают дискретные энергетические уровни. При этом, в соответствии с принципом Паули, на каждом уровне находится не более двух электронов с противоположно направленными спинами. При объединении N атомов в кристалл количество электронов, претендующих расположиться на одном энергетическом уровне кристалла, который при обобществлении электронов следует рассматривать как единую квантово-механическую систему, увеличивается в N раз, а "вместимость" уровня по-прежнему не превышает двух. Заполнение более высоких уровней не выгодно с энергетической точки зрения. В результате вместо дискретного энергетического уровня изолированных атомов в кристалле образуется энергетическая зона, занимающая целый интервал энергий и состоящая из N близко расположенных уровней.
На языке квантовой физики это означает расщепление энергетического уровня атомов в кристалле в зону. В этом состоит наиболее характерное отличие энергетического спектра кристалла от спектра изолированного атома.
При сближении атомов происходит не только расщепление энергетических уровней в зоны, но и некоторое смещение их энергетического положения вследствие взаимодействия атомов.
Ширина энергетической зоны может быть оценена, исходя из соотношения неопределенностей для энергии и вре-
46
мени: Е |
h |
, где W - длительность пребывания электрона |
|
||
τ |
|
|
вблизи ядра некоторого атома (неопределенность во времени, когда происходит туннельный переход электрона от атома к атому) и для валентных электронов составляет, как правило, величину порядка 1эВ.
Учитывая, что в кристалле объемом 1 см3 содержится 1022 атомов, расстояние между уровнями в зоне ~ 10-22 эВ. Столь малая разность энергий уровней в зоне позволяет считать плотность электронных состояний в энергетической зоне квазинепрерывной.
Поскольку вероятность туннелирования (величина 1/W) экспоненциально сильно убывает с увеличением высоты и ширины потенциального барьера, ширина энергетических зон для внутренних электронов мала. Энергетический спектр этих необобществленных электронов, как уже отмечалось, остается практически таким же, как и в изолированных атомах, то есть представляет собой дискретные энергетические уровни. Электроны внутренних уровней можно считать локализованными на узлах решетки и рассматривать ядро вместе со всеми внутренними электронами как единый атомный остов (ион данного элемента).
47

2.2. Уравнение Шредингера для электронов в кристалле. Основные допущения зонной теории
Подобно определению разрешенных уровней энергии электронов в атоме, количественно энергетический спектр электронов в твердом теле определяется посредством решения уравнения Шредингера.
Стационарное уравнение Шредингера для кристалла может быть записано в общем случае в виде
− |
h2 |
∑ i2 Ψ − |
h2 |
∑ |
1 |
α2 Ψ +UΨ = EΨ, |
(2.1) |
|
2m |
2 |
|
||||||
|
i |
|
α |
Mα |
|
|||
где Ψ = Ψ(rr1 ,...rri ,...rrn , Rs1 ,...Rrα ,...Rn ) - |
волновая функция, |
зависящая от |
||||||
координат (радиуса-вектора) |
всех электронов rri и атомных ядер |
|||||||
(остовов)
U - потенциальная энергия, которая складывается из энергий попарного взаимодействия электронов с электронами, ядер с ядрами и электронов с ядрами:
U = |
1 |
∑ |
|
|
e2 |
|
|
|
|
|
|
|
1 |
∑ |
Z |
Z |
|
e2 |
|
|
|
1 |
∑ |
Z |
|
e2 |
|
|
(2.2) |
|||||
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
k |
rm |
r |
|
|
− |
|
|
|
k |
r |
|
|
||||||||
2 |
4πε |
|
ε |
|
r |
r |
|
|
|
|
|
4πεε |
|
2 |
4πεε |
|
|
r |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
i, j |
0 |
|
r |
− r |
j |
|
|
|
|
|
2 k ,m |
0 |
R |
k |
− R |
m |
|
|
i,k |
0 |
|
r |
− R |
k |
|
|
|||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(коэффициент 1/2 учитывает то обстоятельство, что при суммировании по всем частицам потенциальная энергия каждого парного взаимодействия входит в суммудважды);
m и Ма - массы электрона и атомных ядер соответственно. Решение данного уравнения позволяет в принципе получать
все необходимые сведения о кристалле: разрешенные значения энергии электронов (используя естественные ограничения, накладываемые на волновую функцию), координаты атомных остовов (интегрируя \(ri,Ra) по координатам всех электронов и определяя Ra , отвечающие максимуму полученного распределения вероятно-
48
стей, возможных для данной энергии пространственных распреде-
лений ядер), |
распределение электронной плотности (вычис- |
||||
ляя |
|
Ψ(rri ) |
|
2 Rα , |
где Ra - координаты ядер, соответствующие |
|
|
||||
определенной кристаллической решетке).
Однако в общем случае задача является безнадежно сложной. Это связано с тем, что волновая функция \ зависит от огромного числа независимых переменных (по порядку величины не ниже 1023 см-3 ). Для приближенного ее решения делается ряд упрощающих допущений.
Первое допущение состоит в рассмотрении кристалла как системы, состоящей из двух независимых подсистем - быстрых электронов и практически неподвижных ядер. Оно основывается на том, что масса ядер значительно больше массы электронов. Поскольку в термодинамическом равновесии кинетические энергии тех и других частиц одного порядка, скорости электронов оказываются приблизительно на два порядка величины больше, чем скорости ядер. Таким образом, для любой конфигурации ядер в твердом теле будет успевать устанавливаться соответствующее ей равновесное состояние электронной подсистемы.
Это означает, что в каждый момент времени можно рассматривать движение электронов в поле фиксированных ядер. Напротив, движение ядер можно рассматривать не в поле мгновенной конфигурации электронов, а в поле, создаваемом усредненным пространственным распределением их зарядов.
Такое представление исключает возможность обмена энергии между электронной и ядерной подсистемами (электронно-фононное взаимодействие). В этой связи данное допущение называется адиа-
батическим приближением.
В адиабатическом приближении движение электронов и ядер можно считать независимым и, следовательно, волновую
49

функцию системы можно представить в виде произведения волновых функций электронной и ядерной подсистем:
Ψ(rri Rα )= Ψe (rri Rα )ξ(Rα ) . |
(2.3) |
Заметим, что в электронной волновой функции ψе координаты ядер Ra уже не переменные, а параметры.
Подставляя это выражение для ψ в уравнение Шредингера для кристалла, разделяем его на два независимых уравнения, описывающих движение ядер и электронов в кристалле.
Последнее из них имеет вид:
|
h2 |
∑i |
2 |
1 |
∑i, j |
|
e2 |
|
|
|
|
|
|
1 |
∑i,k |
Zk e2 |
|
|
|
Ψe = Ee Ψe . |
||||||
− |
|
i ψe + |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
− Rr |
|
|
|
||||
2m |
2 |
4πε |
ε |
|
rr |
− rr |
|
|
|
|
2 |
4πεε |
0 |
|
rr |
k |
||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
i |
j |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.4)
Видно, что благодаря адиабатическому приближению, задачу о системе ядер и электронов удалось свести к более простой задаче о движении только электронов в заданном поле ядер (координаты ядер входят в уравнение теперь только как параметры задачи, от которых зависит потенциальная и полная энергии электронов).
Однако, упрощая задачу, адиабатическое приближение не снимает основной трудности ее решения: задача по-прежнему остается задачей многих тел.
Для того чтобы свести задачу о движении многих электронов к задаче движения одного, отдельно взятого электрона, используют следующее так называемое одноэлектронное приближение.
Вместо того, чтобы рассматривать взаимодействие данного электрона с каждым из остальных электронов системы, полагают, что этот электрон движется в некотором результирующем поле, созданном эффективным зарядом остальных электронов, определенным образом распределенных в пространстве. Вместо переменного по време-
50

ни электрического поля рассматривается постоянное усредненное поле.
Такой подход |
позволяет заменить в уравнении |
Шредин- |
|||||||||||
|
|
1 |
|
|
|
2 |
|
|
|
|
|
||
|
∑ |
|
|
e |
|
|
|
|
|
|
|||
|
2 |
4πε |
|
ε |
|
r |
r |
|
|
||||
|
|
|
|
|
|
||||||||
|
|
|
|
||||||||||
|
i, j |
0 |
|
r |
− r |
j |
|
|
|
||||
гера для электронов |
в кристалле двойную сумму |
|
|
|
|
i |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
(потенциальную энергию межэлектронного взаимодействия) на член
вида |
∑U ′(rri |
) |
U ′( ri ) -потенциальная энергия i-го электрона в |
i |
, где |
эффективном поле всех остальных электронов, в котором каждый электрон движется независимо. Таким образом, в одноэлектронном приближении система взаимодействующих между собой электронов сводится к газу невзаимодействующих частиц (квазичастиц), который обладает более сложным законом дисперсии, чем свободные электроны.
Если учесть, что заряд каждого электрона "размазан" в про-
странстве с плотностью |
|
Ψ(rr) |
|
2 |
|
|
, то потенциальную энергию U'(rt) |
|||||||||||
|
|
|
|
|||||||||||||||
|
|
|
||||||||||||||||
можно определить как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
r |
|
|
Ψj (rr) |
|
2 |
|
|
|
r |
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||
U ′(ri ) = ∑e2 |
∫ |
|
|
|
|
rr |
|
− rr |
|
|
drj |
|
|
|||||
4πεε |
0 |
|
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
j |
i |
|
|
. |
(2.5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Данное выражение называется потенциалом Хартри.
Таким образом, уравнение Шредингера для электронной подсистемы кристалла можно записать в виде
|
h2 |
|
r r |
|
r |
|
|
− |
|
∑ i2 + ∑U (ri , Rα ) + ∑U ′(ri ) Ψe = Ee Ψe |
|
|
|||
2m |
|
|
|||||
|
i |
i |
i |
|
. |
(2.6) |
|
|
|
|
|
|
|
||
Представляя волновую функцию электронной подсистемы кристалла в виде произведения одноэлектронных функций
51

|
|
|
ψe = ΠΨi (ri ) |
|
(2.7) |
|
и подставляя ее в (2.6), получаем N независимых одинаковых уравне- |
||||||
ний (N -количество электронов) для каждого электрона: |
|
|||||
|
|
h2 |
r r |
r |
|
|
|
− |
|
i2 Ψi + [U (ri, Rα ) +U ′(ri ) Ψi |
= Ei Ψi |
|
|
|
2m |
|
||||
|
|
|
|
|
(2.8) |
|
|
|
|
|
|
|
|
|
где |
Еi |
- собственное значение энергии 1-го электрона. |
|||
При |
этом |
энергия |
электронной |
подсистемы |
кристалла |
|
Ее = ∑Ei .Полученное уравнение называется уравнением Хартри.
i
Таким образом, благодаря сделанному допущению, удалось свести задачу решения уравнения Шредингера для системы электронов к одноэлектронной задаче.
Обратим внимание на то, что хотя волновая функция
ψe = ΠΨi (ri ) и является решением уравнения Шредингера в одно-
электронном приближении, она не удовлетворяет принципу Паули (то есть эта функция не обращается в нуль, когда два электрона оказываются в одном и том же состоянии) и не подчиняется статистике Ферми, согласно которой волновая функция должна быть антисимметричной относительно перестановки двух электронов местами.
Указанным требованиям удовлетворяет волновая функция электронной подсистемы, задаваемая так называемым определителем Слэтера:
|
|
|
Ψ1 |
(rr1 ) |
Ψ1 |
(rr2 ) .... |
Ψ1 |
(rrN ) |
|
||
ψ |
|
= |
1 Ψ2 |
(rr1 ) |
Ψ2 |
(rr2 ) .... |
Ψ2 |
(rrN ) |
|
||
e |
N! .... |
.... |
.... |
... , |
(2.9) |
||||||
|
|
||||||||||
|
|
|
|||||||||
|
|
|
ΨN (rr1 ) ΨN (rr2 ) .... ΨN (rrN ) |
|
|||||||
где N - число электронов в системе. |
|
|
|
||||||||
52
