2.10. Управление технологическим процессом и оценка его возможностей

Для управления процессами используют статистические сигналы о наличии особых (н е с л у ч а й н ы х) причин вариаций. Постоянное установление, а затем и устранение этих особых причин чрезмерной изменчивости процесса приводит его в состояние статистической управляемости. Если процесс находится в статистически управляемом состоянии, качество продукции предсказуемо, и процесс пригоден для удовлетворения требований, установленных в нормативных документах.

Наиболее часто используют две карты (средних и размахов). Они отражают четыре варианта условий протекания техпроцесса:

1. Среднее неуправляемо	Размах управляем	Процесс неуправляем
2. Среднее управляемо	Размах неуправляем
3. Среднее неуправляемо	Размах неуправляем
4. Среднее управляемо	Размах управляем	Процесс управляем

Проиллюстрируем эти варианты:

а) среднее процесса неуправляемо (рис. 14):

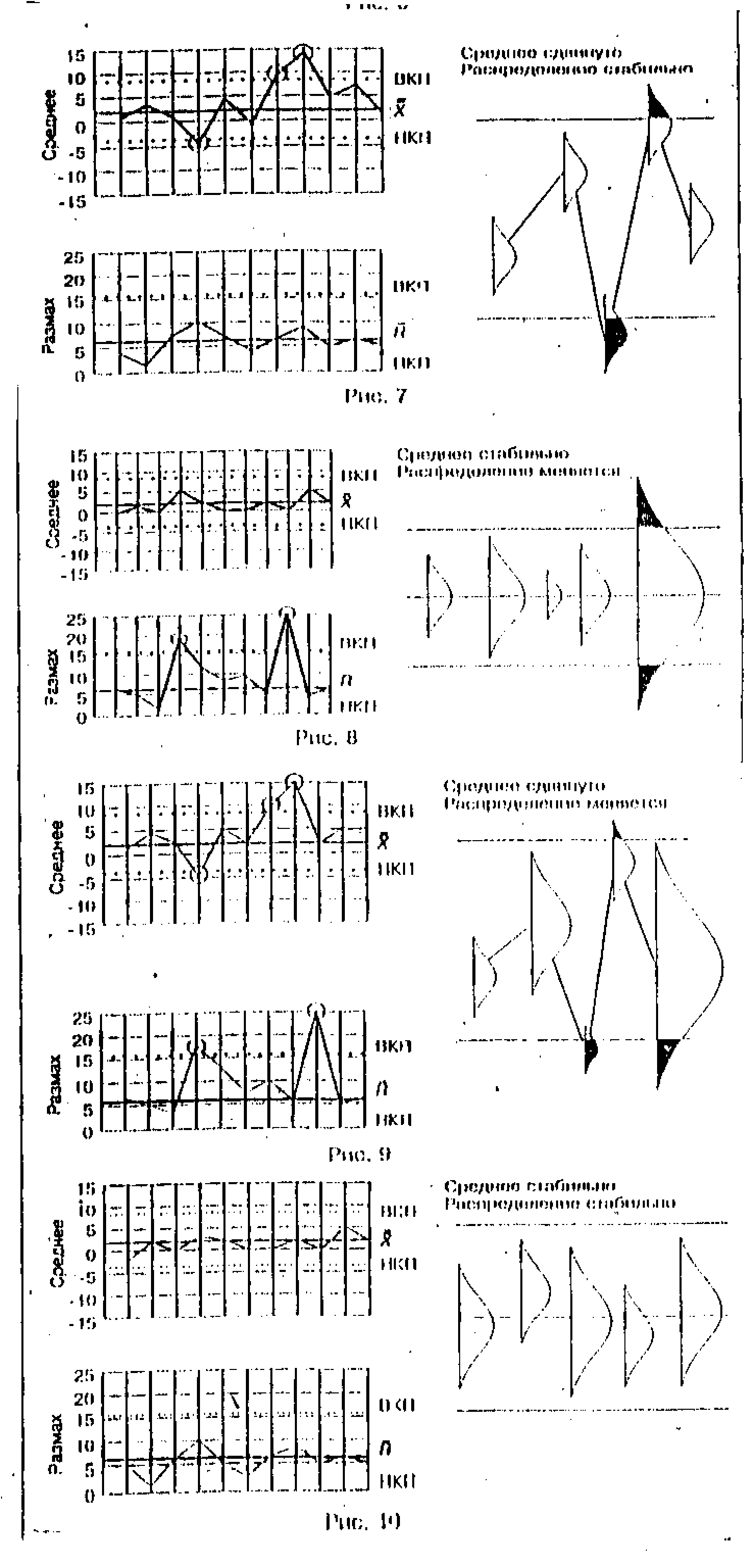
Рис. 14.

Не управляемый процесс,

т.к. неуправляемо среднее значение параметра

б) вариабельность процесса неуправляема(рис. 15):

Рис. 15.

Не управляемый процесс,

т.к. неуправляема вариабельность параметра

в) неуправляемы как среднее, так и вариация процесса(рис. 16):

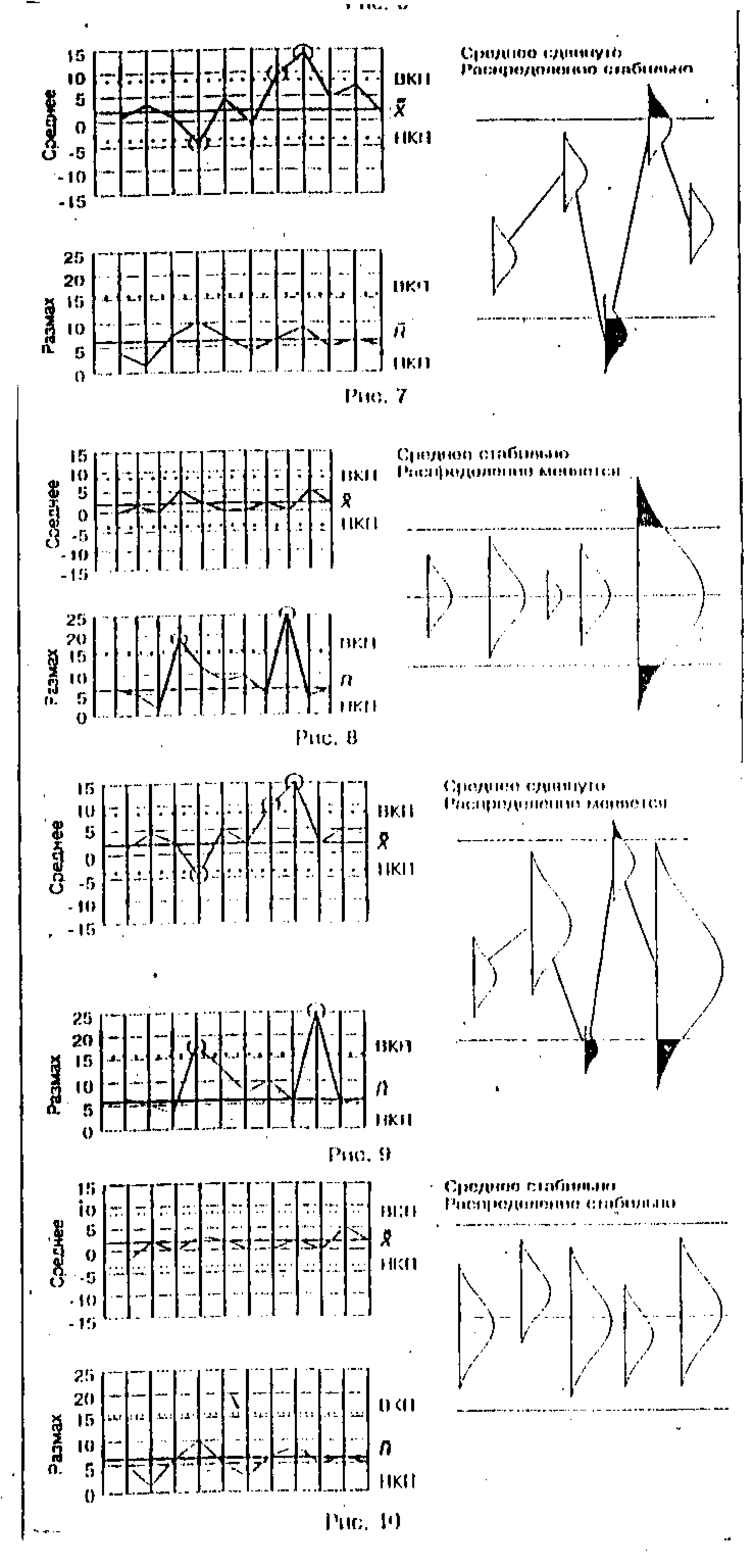
Рис. 16.

Не управляемый процесс,

т.к. неуправляемы и среднее, и размах параметра

г) процесс управляем(рис. 17):

Рис. 17.

Управляемый процесс,

т.к. управляемы и среднее, и размах параметра

Кроме контрольных карт для оценки техпроцесса используется показатель возможностей процесса(или мощности процесса). По его значению можно делать заключение о связи разброса и допуска.

В общем случае возможности процесса оцениваются с помощью индекса С _р:

C _р=

где UTL– верхнее предельно допустимое значение параметра;

LTL– нижнее предельно допустимое значение параметра;

- оценивают дисперсию по средней изменчивости внутри под-

групп и выражают как /c ₄или/d ₂.

При С _р< 1 возможности процесса считаются неприемлемыми. При

С _р= 1 процесс находится на грани требуемых возможностей. На практике

в качестве минимально приемлемого значения берётся С _р= 1,33 , так как в выборках всегда есть вариация данных, и нет процессов, которые находились бы всегда в статистически управляемом состоянии (более подробно об этом ниже).

3. Корреляционно-регрессионный анализ

3.1. Диаграмма разброса (корреляционный анализ)

Диаграмма разброса, также как и метод расслоения, используется для выявления причинно-следственных связей показателей качества и влияющих факторов при анализе причинно-следственной диаграммы, например, между параметрами качества стекломассы (плотность, однородность и др.) или ленты стекла (толщина, разнотолщинность, кривизна, величина торцевых напряжений и др.) и технологическими параметрами варки и выработки (температура, скорость и др.). Анализ диаграмм разброса или оценка корреляционной взаимосвязи параметров является важнейшей частью корреляционно-регрессионного анализа.

Диаграмма разброса строится как график корреляции между двумя параметрами: оба параметра качества, один параметр качества – другой технологический параметр, оба параметра техпроцесса. С помощью диаграммы выясняется, имеется ли между этими двумя параметрами корреляционная зависимость (иначе говоря, взаимосвязанная изменчивость). Если усматривается наличие такой зависимости, то считают, что причинный параметр оказывает большое влияние на характеристику. А это значит, что удерживая этот параметр под контролем, можно достичь стабильности характеристики. Наличие взаимосвязи между исследуемыми параметрами облегчает контроль процесса производства с технологической, временно'й и экономической точек зрения. Зная характер взаимосвязи, можно осуществлять контроль только одного из двух параметров; нет необходимости в приборном контроле за другим параметром.

Для построения диаграммы разброса с целью определения зависимости между двумя видами данных сначала проводят сбор этих данных и представляют их в виде таблицы (например, табл. 6.) В ней: F – содержание в стекле оксида Fe ₂O ₃, мас.%, и D – светопропускание стекла в ИК-области спектра, % ).

Таблица 6.

Выборка для оценки связи между светопропусканием

стекла и содержанием в нём оксида железа

№ изме- рения	F	D	№ изме- рения	F	D
1	0,28	64,7	14	0,28	63,4
2	0,28	65,9	15	0,28	62,9
3	0,295	64,3	16	0,27	64,9
4	0,29	62,9	17	0,28	64,3
5	0,28	63,6	18	0,27	64,4
6	0,3	61,8	19	0,275	64,5
7	0,3	61,5	20	0,285	63,1
8	0,29	62,8	21	0,295	62,6
9	0,29	63,2	22	0,27	66,2
10	0,29	63,5	23	0,285	62,9
11	0,3	62,9	24	0,295	61,8
12	0,29	64,1	25	0,285	64,4
13	0,28	63,5	26	0,275	65,5

Далее данные в порядке измерения наносятся на график (например, см. рис. 18).

По диаграмме можно увидеть, имеется ли между двумя параметрами корреляционная зависимость. О наличии такой связи можно уверенно говорить, когда разброс данных имеет линейную тенденцию.

Представленные диаграммы разброса на рис. 19 демонстрируют характер корреляционной зависимости, возможный при оценке взаимосвязи

Р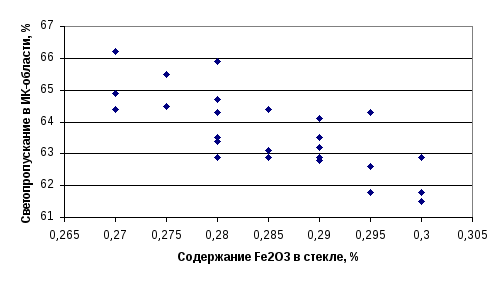ис. 18.

Пример диаграммы разброса

на основании данных таблицы 10

различных параметров, т.е. дают представление о том, как будет изменяться один параметр при определённом изменении другого.

Так, корреляция может быть п р я м о й (при увеличении одного параметра увеличивается и другой, см. рис. 20 А и Б ) ио б р а т н о йили отрицательной (при увеличении одного параметра другой при этом уменьшается, см. рис. 19 В). Корреляция может бытьт е с н о й(сильной) илил ё г к о й(слабой), см. рис. 19. А и Б, В. Наконец, корреляция может бытьк р и в о л и н е й н о й(рис. 19 Д и Е)

Оценивают степень тесноты (значимость) корреляционной зависимости различными методами. Так, можно вычислить коэффициент корреляциипо формуле:

r=,

гдеx _i иy _i– значения параметровхиудляi-го измерения;

,- средние арифметические значения величинх иу;

S _x,S _y– стандартные отклонения величинхиу;

n– число измерений в выборке (объём выборки).

Чем ближе коэффициент корреляции к ±1, тем теснее зависимость между параметрами. Если r= 0 , корреляционная зависимость отсутствует.

Более простым методом анализа корреляционной зависимости является метод медиан. На диаграмме разброса (например, на рис. 21 [8]) проводится вертикальная линия медианы и горизонтальная линия медианы. Выше и ниже горизонтальной медианы, справа и слева от вертикальной медианы должно быть равное число точек. Если число точек нечётное, одна из медиан проходит через центральную точку.

В каждом получившихся при разделении квадрантов подсчитывается число точек и обозначают их соответственно n ₁, n ₂,n ₃ ,n ₄ . Точки, через которые прошла медиана, не учитывают. Отдельно складывают точки в положительных и отрицательных квадрантах:

n ₍₊₎ =n ₁+n ₃= 9 + 9 = 18;

n _(-) =n ₂+n ₄= 2 + 2 = 4;

k=n ₍₊₎ +n _(-)= 18 + 4 = 22.

Так как три точки находятся на медианах, kне равноn= 25.

Для определения наличия и степени корреляции по методу медианы используется таблица кодовых значений, соответствующих различным kпри двух значениях уровня значимости (коэффициента риска) α / 0,01 и 0,05 / (см.табл. 7 [8]).

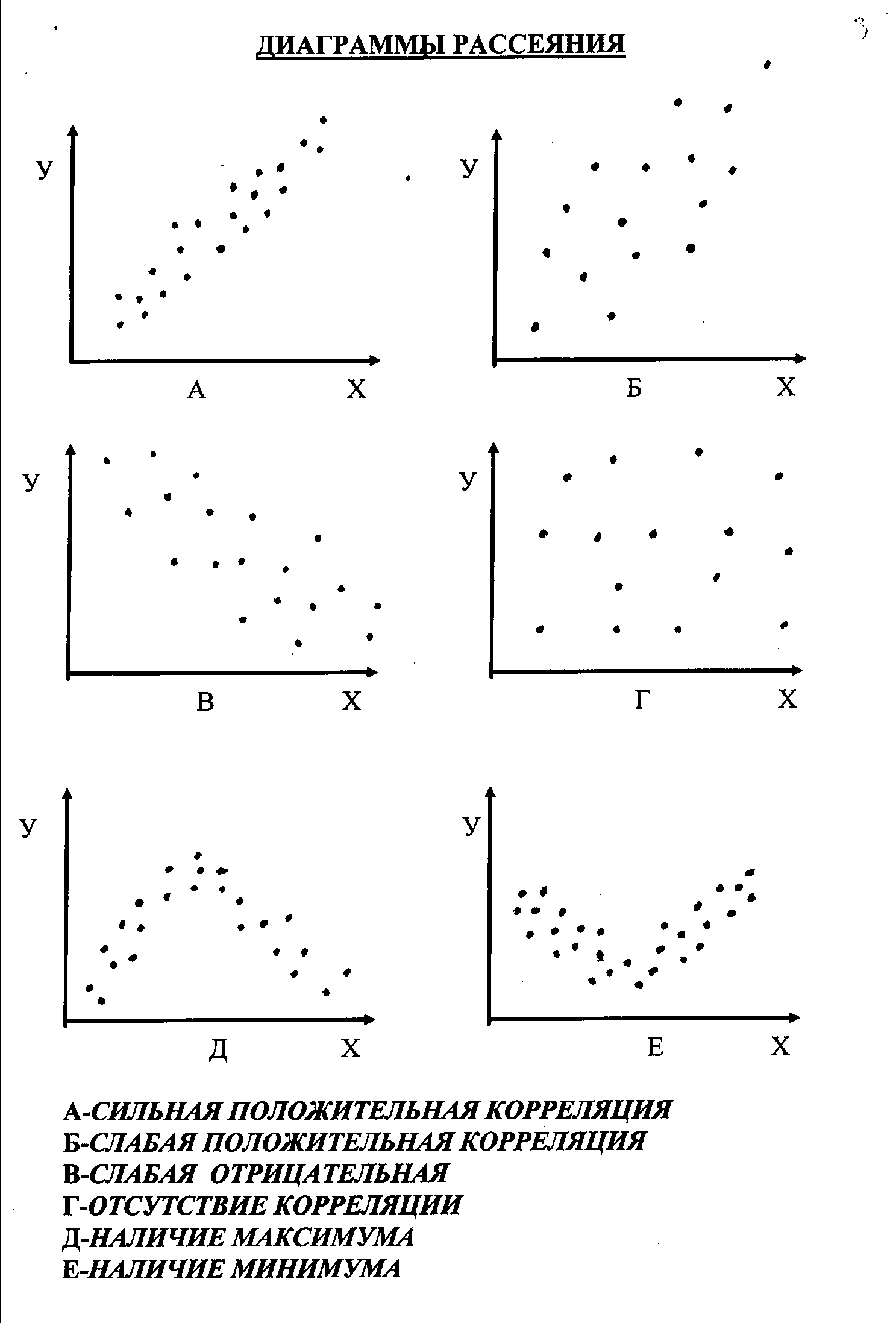
Рис. 19.

Диаграммы разброса

( А – сильная положительная или прямая корреляция, Б – слабая положительная корреляция, В – слабая отрицательная или обратная корреляция, Г – отсутствие корреляции, Д и Е – варианты криволинейной корреляции )

Рис. 20.

Определение корреляции между параметрами

методом медиан

Сравнивая меньшее из чисел n ₍₊₎иn _(-)cкодовым значением из табл. 7 , соответствующим значениюk, делают заключение о наличии и характере корреляции. Если меньшее из чиселn ₍₊₎иn _(-)оказывается равным или меньше кодового значения, то корреляционная зависимость имеет место. В рассматриваемом примере табличное кодовое значение при уровне значимости α = 0,01 , соответствующее k = 22, равно 4. Поскольку меньшим является значение n _(-)= 4 , можно утверждать, что в данном случае между двумя параметрами существует корреляционная зависимость с коэффициентом риска 1%. Поскольку n ₍₊₎> n _(-), это свидетельствует о прямой корреляции. А если бы n ₍₊₎было меньше n _(-), мы говорили бы об обратной корреляции.

В тех случаях, когда характеристика (результат) у и влияющий на неё фактор (причина)хконтролируются с помощью временных графиков или контрольных карт, заключение о наличии или отсутствии корреляции между ними может быть сделано и без построения диаграммы разброса, а только на основании сравнения соответствующих кривых (см. пример из работы [8] на рис. 21 ) или сравнения самих данных измерений (см. табл. 8).

При сравнении графиков на них проводятся линии медиан, разделяющие график так, что точки графика распределяются поровну выше и ниже соответствующей медианы (в таблицах рассчитываются значения Ме ).

k	α			α			α
	0,01	0,05	k	0,01	0,05	k	0,01	0,05
8	0	0	37	10	12	66	22	24
9	0	1	38	10	12	67	22	25
10	0	1	39	11	12	68	22	25
11	0	1	40	11	13	69	23	25
12	1	2	41	11	13	70	23	26
13	1	2	42	12	14	71	24	26
14	1	2	43	12	14	72	24	27
15	2	3	44	13	15	73	25	27
16	2	3	45	13	15	74	25	28
17	2	4	46	13	15	75	25	28
18	3	4	47	14	16	76	26	28
19	3	4	48	14	16	77	26	29
20	3	5	49	15	17	78	27	29
21	4	5	50	15	17	79	27	30
22	4	5	51	15	18	80	28	30
23	4	6	52	16	18	81	28	31
24	5	6	53	16	18	82	28	31
25	5	7	54	17	19	83	29	32
26	6	7	55	17	19	84	29	32
27	6	7	56	17	20	85	30	32
28	6	8	57	18	20	86	30	33
29	7	8	58	18	21	87	31	33
30	7	9	59	19	21	88	31	34
31	7	9	60	19	21	89	31	34
32	8	9	61	20	22	90	32	35
33	8	10	62	20	22	91	32	35
34	9	10	63	20	23	92	33	36
35	9	11	64	21	23	93	33	36
36	9	11	65	21	24	94	34	36

Таблица 7.

Кодовые значения для оценки степени корреляции методом медиан

Придаётся точкам со значениями бо'льшими, чем значения медиан, знак (+), а точкам со значениями меньшими, чем у медиан, знак (-); точкам, находящимся на линиях медиан на графиках, или равных по значению медианам в таблицах, присваивается знак (0).

Далее записывается ряд знаков, полученных в результате последовательного перемножения знаков обоих параметров, причём если знаки у параметров хиуодинаковы, произведениех_* уполучает знак (+), если разные – знак (-), а если одно из значений (или х, илиу) имеет знак (0), то и произведениех*уполучает знак (0).

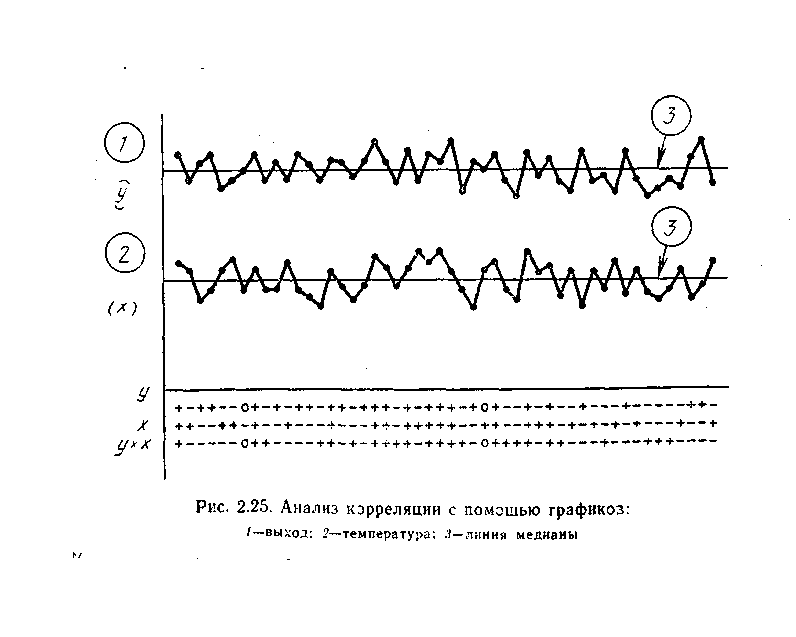
Рис. 21.

Оценка степени корреляции между параметрами

по их временным рядам.

( 1 – выход продукта, 2 – температура, 3 – линия медианы )

Теперь складываем число знаков (+), число знаков (-) и число знаков (0) и обозначаем их как n'₍₊₎, n'_(-), n'₀. Определяем n ₍₊₎и n_(-)(например для данных из табл. 10):

n ₍₊₎ =n'₍₊₎+n'₀/ 2 = 4 + 5/2 = 6,5;

n _(-)=n'_(-)+n'₀/ 2 = 17 + 5/2 = 19,5.

Определяем k= n ₍₊₎ + n _(-)= 6,5 + 19,5 = 26. Меньшее из чисел n ₍₊₎и n _(-)сравниваем с кодовым значением из табл. 7 , соответствующимk, и делаем заключение о наличии или отсутствии корреляции. В нашем примере меньшее из двух чисел n ₍₊₎= 6,5. Из таблицы видим, что кодовое число дляk= 26 при уровне значимости (коэффициенте риска) 0,05 равно 7. Посколькуn ₍₊₎= 6,5 < 7 , можно сделать вывод о наличии корреляции между параметрами F и D , причём отрицательной и относительно слабой. Кстати, расчётный коэффициент корреляции r = - 0,751 тоже говорит о легкой корреляции между рассматриваемыми параметрами.

Таблица 8.

Оценка корреляции между светопропусканием стекла (D)

и содержанием в нём оксида железа (F) методом медиан

№ изме- рения	F	D	Сравнение F с Ме	Сравнение D с Ме	F*D
1	0,28	64,7	-	+	-
2	0,28	65,9	-	+	-
3	0,295	64,3	+	+	+
4	0,29	62,9	+	-	-
5	0,28	63,6	-	+	-
6	0,3	61,8	+	-	-
7	0,3	61,5	+	-	-
8	0,29	62,8	+	-	-
9	0,29	63,2	+	-	-
10	0,29	63,5	+	0	0
11	0,3	62,9	+	-	-
12	0,29	64,1	+	+	+
13	0,28	63,5	-	0	0
14	0,28	63,4	-	-	+
15	0,28	62,9	-	-	+
16	0,27	64,9	-	+	-
17	0,28	64,3	-	+	-
18	0,27	64,4	-	+	-
19	0,275	64,5	-	+	-
20	0,285	63,1	0	-	0
21	0,295	62,6	+	-	-
22	0,27	66,2	-	+	-
23	0,285	62,9	0	-	0
24	0,295	61,8	+	-	-
25	0,285	64,4	0	+	0
26	0,275	65,5	-	+	-
Ме	0,285	63,5