2.6. Сравнение выборок
При предварительном анализе данных наблюдений часто возникает необходимость сравнения двух или нескольких выборок данных, полученных в относительно разных условиях, чтобы решить одинаковы ли они, принадлежат ли одной генеральной совокупности, и тогда эти выборки при необходимости можно объединять для последующего анализа более мощного массива данных; или же выборки неодинаковы, а значит разница между ними не случайна и выборки не могут быть объединены.
Сравнивают выборки по их средним значениям [ 2 ]. Однако это сравнение производится по-разному в зависимости от того, как соотносятся между собой дисперсии этих выборок. Поэтому вначале определяют равны или не равны эти дисперсии.
а) Сравнение двух дисперсий
В качестве характеристики проверки гипотезы о равенстве дисперсий используется частное несмещённых оценок дисперсий генеральной совокупности:
,
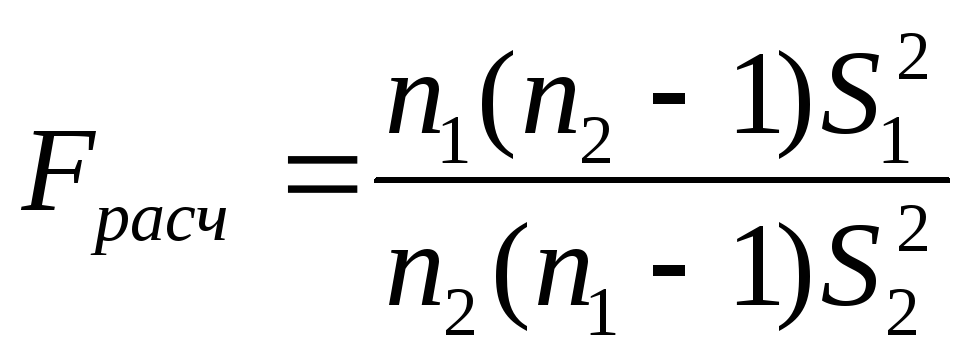где в числителе должна быть бо'льшая из двух оценок рассеяния (для того, чтобы значение Fрасчвсегда было больше 1).
Доказано, что характеристика FимеетF-распределение с (n 1– 1) и (n 2 – 1) степенями свободы. Критическая область для проверяемой гипотезы при уровне значимости α является односторонней и определяется соотношениемF расч иF α. Величину F αопределяем при уровне значимости α = 0,05 или α = 0,01 из Приложения 1.
Если F расч < F α, значит дисперсии равны (при этом не значит, чтобы были одинаковыми их численные выражения); если же F расч> F α, то дисперсии считаются не равными, и значит разница между выборками не случайна, и существуют какие-то для этого причины.
Например,
сравним работу за месяц двух смен цеха
флоут-стекла по производительности
(съёму) процесса. Показатели работы
смены № 1 –
1= 101,29 т/сут;S21 =
0,0729 т/сут;n 1 = 16 смен;
соответственно у смены № 2 -
2
= 101,69;S22 =
0,1369;n 2 = 14. Каждую
группу можем считать случайной выборкой
из нормальной генеральной совокупности.
По таблице F-распределения найдём при уровне значимости α = 0,05 и 16-1=15 и 14-1=13 степенях свободыF0,05= 2,53. Подсчитаем величинуF расч = 14ּ15ּ0,1369 / 16ּ13ּ0,0729 = 1,896. ПосколькуF расч<F 0.05, то делаем вывод: существенной разницы между дисперсиями генеральных совокупностей не обнаружено и, следовательно, для сравнения средних арифметических можно применитьt-критерий
б) Сравнение среднеарифметических при равных дисперсиях.
В качестве характеристики сравнения рассчитывают величину
.
Выборки считаются равными, если расчётная величина tоказывается больше, чем (-tα), и меньше, чем (t α), т.е. находится внутри диапазона: - t α< t расч < t α.
Величина t αнаходится по таблице дляt– распределения (см. Приложение 2) при уровне значимости α и числе степеней свободы
n 1+ n 2– 2.
Продолжим сравнение выборок из предыдущего примера. По таблице t-распределения при α = 0,05 и 16 + 14 – 2 = 28 степенях свободы
t
0.05= 2,048. Следовательно, критическая
область определяетсяt< -2,048 иt>2,048. На основании
данных выборок рассчитаем величину
характеристики
-1,353. Поскольку эта величина попадает в
критическую область (t=
-1,353 < -2,048 ), значит сравниваемые выборки
равны по своим средним арифметическим,
разница между ними случайна и причины
её не существенны.
в) Сравнение среднеарифметических при неравных дисперсиях.
При неравных дисперсиях среднеарифметические двух выборок сравнивают способом, также основанном на t– распределении, для которого двусторонняя симметричная критическая область определяется следующим образом.
Сначала рассчитывают величину t'по формуле:
,
которую сравнивают с величиной t", определяющей критическую область и рассчитываемой по формуле:
,
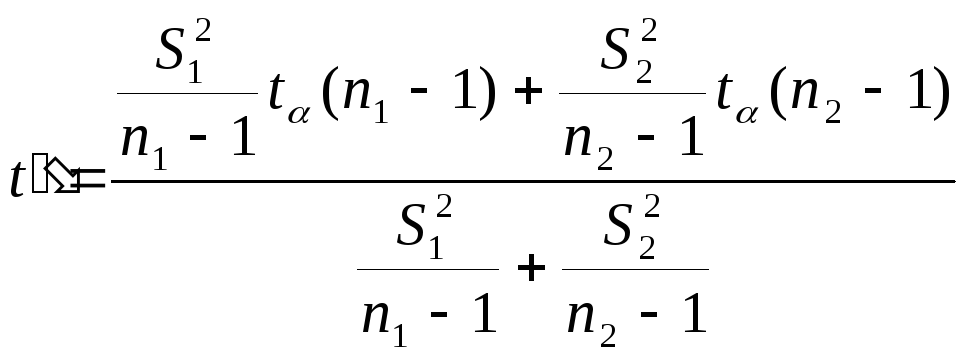где t α(n 1– 1) – значение при n 1– 1 степенях свободы и уровне значимо-
сти α ; t α(n 2– 1) – значение приn 2– 1 степенях свобо-
ды и уровне значимости α . Эти значения находят в таб-
лице (см. Приложение 2).
В результате, если расчётная величина t'< t", то с полным основанием можно говорить о равенстве сравниваемых среднеарифметических.
В качестве
примера сравним выработки листового
стекла марки М-1 дневной (с 8-00 до 20-00 час)
и ночной (с 20-00 до 8-00 час) смен в течении
месяца. Параметр выражается в процентах
полученного сортового стекла от
сформованного. Характеристики работы
дневной смены:
1=
48,35 %;S21 = 289;n 1 = 31; соответственно
у ночной -
2
= 50,63 %;S22 =
150;n 2 = 31.
Сначала сравним выборки по дисперсиям. По таблице F-распреде –
ления находим
при уровне значимости α = 0,05 и 31-1=30 и
31-1=30 степенях свободы F0,05 = 1,84.F расч =
.
ПосколькуF расч >F α , то дисперсии
считаются неравными и сравнение средних
арифметических производят по приближённомуt- критерию.
По таблице t– распределения при 5%-ном уровне значимостиt 0,05для обоих выборок одинакова и равна 2,042. Определим критическую область:
t"
=
,
аt' =
,
то есть
t' < t" и значит средние арифметические сравниваемых выборок одинаковы.
Общий вывод: хотя в дневную смену есть причины для большей вариации технологического процесса, в среднем за данный месяц практически не отстала от ночной смены.
Примером анализа работы цеха можно взять сравнение выборок результатов работы смен и бригад (пример 4 из «Практикума»).
Сравнение результатов работы бригад показывает
-
Бригада
Ср. знач. съёма, %
Станд.отклон.
1
71.286
9.619
2
69.8
17.827
3
63.344
19.772
4
68.714
16,504
что хуже всех работает 3 бригада.
Среди других версий была сделана попытка оценить, каковы результаты работы 3 бригады после приёма смены от 1, 2 и 4 бригад. В нижеприведённой таблице представлены данные работы цеха за 2 месяца:
-
После 1 бр.
75
75
20,5
66
45
53
64
Сред.
53
После 2 бр.
78
76
79
73
76
37
70
73
70,2
После 4 бр.
76
75
19
71
74
76
65,2
Таким образом, 3 бригада работает хуже после 1 бригады. Причины этого следует искать дальше, в том числе в социальной сфере.