
ЭЛМ_Презентация_10
.pdf
Основные законы магнитного поля
Теорема Гаусса
для вектора
Теорема о циркуляции
вектора
Теорема о
циркуляции в
дифференциальной форме
Понятие вихревого поля
Примеры векторных полей с нулевыми и ненулевыми дивергенциями и роторами
Применение теоремы о циркуляции
вектора
[Парселл Э. Электричество и магнетизм / Берклеевский курс
физики, Т. 2, М.:«Наука», 1975 г., рис. 2.33]
23/36

Основные законы магнитного поля
Теорема Гаусса
для вектора
Теорема о циркуляции
вектора
Теорема о
циркуляции в
дифференциальной форме
Понятие вихревого поля
Примеры векторных полей с нулевыми и ненулевыми дивергенциями и роторами
Применение теоремы о циркуляции
вектора
[Парселл Э. Электричество и магнетизм / Берклеевский курс
физики, Т. 2, М.:«Наука», 1975 г., рис. 2.33]
24/36

Основные законы магнитного поля
Теорема Гаусса
для вектора
Теорема о циркуляции
вектора
Теорема о
циркуляции в
дифференциальной форме
Понятие вихревого поля
Примеры векторных полей с нулевыми и ненулевыми дивергенциями и роторами
Применение теоремы о циркуляции
вектора
[Парселл Э. Электричество и магнетизм / Берклеевский курс
физики, Т. 2, М.:«Наука», 1975 г., рис. 2.33]
25/36

Основные законы магнитного поля
Теорема Гаусса
для вектора
Теорема о циркуляции
вектора
Теорема о
циркуляции в
дифференциальной форме
Понятие вихревого поля
Примеры векторных полей с нулевыми и ненулевыми дивергенциями и роторами
Применение теоремы о циркуляции
вектора
[Парселл Э. Электричество и магнетизм / Берклеевский курс
физики, Т. 2, М.:«Наука», 1975 г., рис. 2.33]
26/36

Основные законы магнитного поля
Теорема Гаусса
для вектора
Теорема о циркуляции
вектора
Теорема о
циркуляции в
дифференциальной форме
Понятие вихревого поля
Примеры векторных полей с нулевыми и ненулевыми дивергенциями и роторами
Применение теоремы о циркуляции
вектора
[Парселл Э. Электричество и магнетизм / Берклеевский курс
физики, Т. 2, М.:«Наука», 1975 г., рис. 2.33]
27/36

6. Применение теоремы о циркуляции
вектора
Основные законы магнитного поля
Теорема Гаусса
для вектора
Теорема о циркуляции
вектора
Теорема о
циркуляции в
дифференциальной форме
Понятие вихревого поля
Примеры векторных полей с нулевыми и ненулевыми дивергенциями и роторами
Применение теоремы о циркуляции
вектора
Идеальный
соленоид
Поле идеального соленоида
Тороидальный
соленоид
Магнитное поле тороидального

Идеальный соленоид
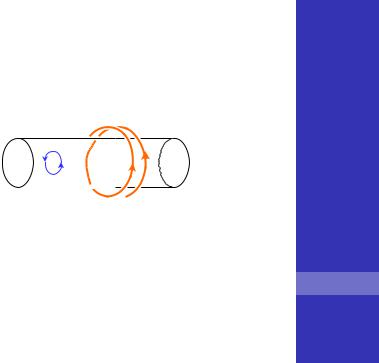
Соленоид представляет собой тонкий провод, намотанный плотно, виток к витку, на цилиндрический каркас, так что число витков, приходящихся на единицу длины цилиндра, постоянно и равно .
I
В соленоиде ток течёт по спирали, так что можно выделить круговую и продольную составляющие тока.
Если витков много, и они расположены плотно друг к другу, то мы можем пренебречь продольным током и рассматривать только круговые токи.
Бесконечно длинный соленоид без продольного тока называют идеальным.
Основные законы магнитного поля
Теорема Гаусса
для вектора
Теорема о циркуляции
вектора
Теорема о
циркуляции в
дифференциальной форме
Понятие вихревого поля
Примеры векторных полей с нулевыми и ненулевыми дивергенциями и роторами
Применение теоремы о циркуляции
вектора
Идеальный
соленоид
Поле идеального соленоида
Тороидальный
соленоид
Магнитное поле тороидального

Идеальный соленоид
Соленоид представляет собой тонкий провод, намотанный плотно, виток к витку, на цилиндрический каркас, так что число витков, приходящихся на единицу длины цилиндра, постоянно и равно .
I
Iкруг Iпрод
В соленоиде ток течёт по спирали, так что можно выделить круговую и продольную составляющие тока.
Если витков много, и они расположены плотно друг к другу, то мы можем пренебречь продольным током и рассматривать только круговые токи.
Бесконечно длинный соленоид без продольного тока называют идеальным.
Основные законы магнитного поля
Теорема Гаусса
для вектора
Теорема о циркуляции
вектора
Теорема о
циркуляции в
дифференциальной форме
Понятие вихревого поля
Примеры векторных полей с нулевыми и ненулевыми дивергенциями и роторами
Применение теоремы о циркуляции
вектора
Идеальный
соленоид
Поле идеального соленоида
Тороидальный
соленоид
Магнитное поле тороидального
Идеальный соленоид
Соленоид представляет собой тонкий провод, намотанный плотно, виток к витку, на цилиндрический каркас, так что число витков, приходящихся на единицу длины цилиндра, постоянно и равно .
I
Iкруг
В соленоиде ток течёт по спирали, так что можно выделить круговую и продольную составляющие тока.
Если витков много, и они расположены плотно друг к другу, то мы можем пренебречь продольным током и рассматривать только круговые токи.
Бесконечно длинный соленоид без продольного тока называют идеальным.
Основные законы магнитного поля
Теорема Гаусса
для вектора
Теорема о циркуляции
вектора
Теорема о
циркуляции в
дифференциальной форме
Понятие вихревого поля
Примеры векторных полей с нулевыми и ненулевыми дивергенциями и роторами
Применение теоремы о циркуляции
вектора
Идеальный
соленоид
Поле идеального соленоида
Тороидальный
соленоид
Магнитное поле тороидального

Идеальный соленоид
Соленоид представляет собой тонкий провод, намотанный плотно, виток к витку, на цилиндрический каркас, так что число витков, приходящихся на единицу длины цилиндра, постоянно и равно .
I
Iкруг
В соленоиде ток течёт по спирали, так что можно выделить круговую и продольную составляющие тока.
Если витков много, и они расположены плотно друг к другу, то мы можем пренебречь продольным током и рассматривать только круговые токи.
Бесконечно длинный соленоид без продольного тока называют идеальным.
Основные законы магнитного поля
Теорема Гаусса
для вектора
Теорема о циркуляции
вектора
Теорема о
циркуляции в
дифференциальной форме
Понятие вихревого поля
Примеры векторных полей с нулевыми и ненулевыми дивергенциями и роторами
Применение теоремы о циркуляции
вектора
Идеальный
соленоид
Поле идеального соленоида
Тороидальный
соленоид
Магнитное поле тороидального
