
- •Содержание
- •1.6.4 Линейная зависимость векторов. Размерность и базис векторного пространства
- •2 Содержание практических занятий
- •3 Правила выполнения контрольной работы
- •4 Задачи для контрольной работы
- •5 Решения типовых задач
- •6 Материалы для подготовки к экзамену
- •7 Справочный материал
- •8 Глоссарий (словарь терминов)
ФГБОУ ВПО Вологодская государственная молочнохозяйственная
академия им. Н. В. Верещагина Кафедра высшей математики и физики
"ЛИНЕЙНАЯ АЛГЕБРА"
методическое пособие для студентов экономического факультета (заочная и очно-заочная формы обучения,
направления подготовки 080100 "Экономика", 080200 "Менеджмент")
Вологда Молочное
2012
ÓÄÊ 512.628.2 (071) ÁÁÊ 22.161.6.ð30
Î303
Составитель доктор физико-математических наук, заведующий кафедрой высшей математики и физики
М. Г. Плотников,
Рецензенты
??
??
О303 Линейная алгебра: методическое пособие для студентов экономиче- ского факультета (заочная и очно-заочная формы обучения, направления подготовки 080100 "Экономика", 080200 "Менеджмент") / Сост. М. Г. Плотников, Ю. А. Плотникова. Вологда Молочное: ИЦ ВГМХА, 2012. ?? с.
Составлено в соответствии с требованиями (федеральный компонент) к обязательному минимуму содержания и уровню подготовки бакалавра и дипломированного специалиста по математическому и естественнонаучному циклу с целью оказания помощи при проведении лекций и практических занятий, а также для организации самостоятельной работы при изу- чении курса.
Предназначено для студентов следующих направлений подготовки: 080100 "Экономика", 080200 "Менеджмент".
Публикуется в соответствии с планом издательской деятельности на 2012 год, утвержд¼нным решением Ученого совета 21.12.2011, прот. 11.
ÓÄÊ 512.628.2 (071) ÁÁÊ 22.161.6.ð30
c Плотников М. Г. 2012c ИЦ ВГМХА, 2012
Содержание |
|
Содержание . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
3 |
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
5 |
1. Краткий курс лекций . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
5 |
1.1. Лекция 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
5 |
1.1.1. Прямоугольная (декартова) система координат на плоскости |
5 |
1.1.2. Уравнение линии на плоскости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
5 |
1.1.3. Уравнение прямой на плоскости . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
6 |
1.1.4. Тангенс угла между двумя прямыми на плоскости. Условия |
|
параллельности и перпендикулярности прямых . . . . . . . . . . . |
8 |
1.2. Лекция 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
9 |
1.2.1. Матрицы и их основные виды . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
9 |
1.2.2. Действия над матрицами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
11 |
1.3. Лекция 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
13 |
1.3.1. Определители квадратных матриц . . . . . . . . . . . . . . . . . . . . . . . . . . |
13 |
1.3.2. Свойства определителей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
15 |
1.3.3. Ранг матрицы и его вычисление . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
16 |
1.4. Лекция 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
19 |
1.4.1. Системы линейных уравнений: основные понятия . . . . . . . . . . |
19 |
1.4.2. Обратная матрица и ее нахождение . . . . . . . . . . . . . . . . . . . . . . . . . |
20 |
1.4.3. Решение систем линейных уравнений методом обратной мат- |
|
ðèöû . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
22 |
1.4.4. Решение систем линейных уравнений методом Крамера . . . . |
23 |
1.5. Лекция 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
24 |
1.5.1. Решение систем линейных уравнений методом Гаусса . . . . . . |
24 |
1.6. Лекция 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
29 |
1.6.1. Векторы на плоскости и в пространстве: геометрическая |
|
точка зрения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
29 |
1.6.2. Векторы на плоскости и в пространстве: алгебраическая |
|
точка зрения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
31 |
1.6.3. n-мерные векторы. Векторное пространство . . . . . . . . . . . . . . . . |
33 |
1.6.4. Линейная зависимость векторов. Размерность и базис век- |
|
торного пространства . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
33 |
1.7. Лекция 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
33 |
1.7.1. Собственные значения и собственные векторы матрицы . . . . |
33 |
1.7.2. Пример использования понятий линейной алгебры в эконо- |
|
мических моделях. Линейная модель обмена . . . . . . . . . . . . . . |
36 |
2. Содержание практических занятий . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
38 |
2.1. Занятие 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
38 |
2.2. Занятие 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
38 |
2.3. Занятие 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
39 |
2.4. Занятие 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
40 |
2.5. Занятие 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
41 |
2.6. Занятие 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
41 |
2.7. Занятие 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
42 |
3. Правила выполнения контрольной работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
42 |
3
4. Задачи для контрольной работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 4.1. Действия над матрицами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 4.2. Ранг матрицы и его нахождение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 4.3. Решение систем линейных уравнений методом Гаусса . . . . . . . . . . . 46 4.4. Векторные пространства. Базис. Разложение вектора по базису.
Решение невырожденных систем линейных уравнений методами Крамера и обратной матрицы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
4.5. Элементы аналитической геометрии на плоскости . . . . . . . . . . . . . . . 47 4.6. Системы линейных неравенств . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 4.7. Собственные значения и векторы матрицы . . . . . . . . . . . . . . . . . . . . . . 49
5. Решения типовых задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 5.1. Действия над матрицами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 5.2. Ранг матрицы и его нахождение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51 5.3. Решение систем линейных уравнений методом Гаусса . . . . . . . . . . . 53
5.4.Векторные пространства. Базис. Разложение вектора по базису. Решение невырожденных систем линейных уравнений метода-
ми Крамера и обратной матрицы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56 5.5. Элементы аналитической геометрии на плоскости . . . . . . . . . . . . . . . 60 5.6. Системы линейных неравенств . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63 5.7. Собственные значения и векторы матрицы . . . . . . . . . . . . . . . . . . . . . . 65
6. Материалы для подготовки к экзамену . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67 6.1. Список экзаменационных вопросов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67 6.2. Примерные темы практических задач для экзамена . . . . . . . . . . . . . 68 6.3. Пример экзаменационного билета . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
7. Справочный материал . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69 7.1. Нахождение корней квадратного уравнения . . . . . . . . . . . . . . . . . . . . . 69 8. Глоссарий (словарь терминов) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
Список литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
4

Введение1. Краткий курс лекций
1.1. Лекция 1.
1.1.1. Прямоугольная (декартова) система координат на плоскости.
Прямоугольная (декартова) система координат на плоскости состоит из двух взаимно перпендикулярных осей (ось Ox ось абсцисс è îñü Oy îñü îð-
динат), точки O начала координат, в которой пересекаются оси, а также масштаба. Положение любой точки плоскости однозначно определяется парой чисел (x, y), которые называются координатами точки. На рис. 1 изображены
îñü Ox, îñü Oy, точка O(0, 0), масштаб, точки A(4, 2), B(−1, 3), (6, 0).
Ðèñ. 1.
Пусть на плоскости заданы точки A(x1, y1) è B(x2, y2). Тогда расстояние между точками A è B находится по следующей формуле:
Åñëè C(x3 |
, y3) середина p |
|
|
|
|
|
|
||
|
|
AB, то координаты точки C находятся |
|||||||
|
|AB| = (x2 − x1)2 + (y2 − y1)2. |
(1) |
|||||||
|
отрезка |
|
|
|
|
|
|||
òàê: |
|
x1 + x2 |
|
|
y1 + y2 |
|
|
|
|
|
x3 = |
, |
y3 = |
. |
(2) |
||||
|
|
|
|||||||
|
2 |
|
2 |
|
|
|
|||
1.1.2. Уравнение линии на плоскости.
на плоскости называется уравнение, связывающее переменные x è y и такое, что координаты точек этой линии и
только они удовлетворяют этому уравнению. В общем случае уравнение линии на плоскости имеет вид
F (x, y) = 0.
Выведем уравнение окружности радиуса R с центром в точке
Пусть M(x, y) произвольная точка окружности. Тогда расстояние от точки M до точки M0 постоянно и равно R:
|MM0| = R.
5

Выражая |MM0| через координаты точек M è M0 с помощью формулы (1), получим:
p
(x − x0)2 + (y − y0)2 = R,
(x − x0)2 + (y − y0)2 = R2
уравнение искомой окружности (см. рис. 2).
Ðèñ. 2.
1.1.3. Уравнение прямой на плоскости.
Рассмотрим различные формы записи уравнения простейшей линии на плоскости прямой линии. Уравнение прямой, проходящей через две заданные
точки (x1, y1) è (x2, y2), может быть записано в виде
y − y1 |
= |
x − x1 |
. |
(3) |
y2 − y1 |
|
|||
|
x2 − x1 |
|
||
Общее уравнение прямой можно записать так:
Ax + By + C = 0,
ãäå A, B, C константы, причем A è B не равны нулю одновременно. Подробнее изучим уравнение прямой с угловым коэффициентом
y = kx + b. |
(4) |
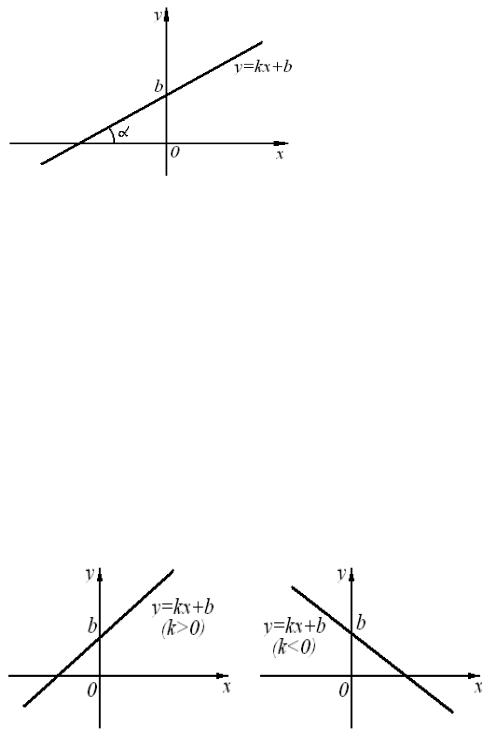
Постоянная k называется угловым коэффициентом прямой и совпадает с тангенсом угла α между прямой и положительным направлением оси Ox (ñì. ðèñ. 3):
k = tg α. |
(5) |
Величина b в уравнении (4) совпадает с ординатой точки пересечения данной прямой и оси Oy (ñì. ðèñ. 3).
Ðèñ. 3.
6
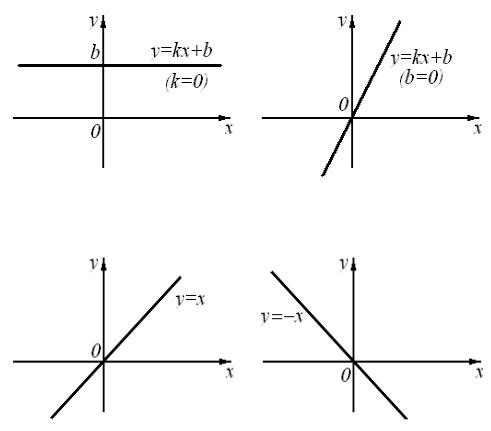
Рассмотрим частные случаи расположения прямой, заданной уравнением (4), на плоскости.
1.Пусть k > 0, тогда (см. формулу (5)) tg α > 0 è óãîë α острый. Схематически такая прямая изображена на рис. 4.
2.Пусть k < 0, тогда (см. формулу (5)) tg α < 0 è óãîë α тупой. Схематически такая прямая изображена на рис. 5.
3.Пусть k = 0, тогда (см. формулу (5)) tg α = 0 è α = 0, то есть прямая параллельна оси Ox (схематически такая прямая изображена на рис. 6).
4.Пусть b = 0, тогда прямая проходит через начало координат (схемати- чески такая прямая изображена на рис. 7).
5.Пусть k = 1, b = 0, то есть уравнение этой прямой имеет вид y = x. Эта прямая проходит через начало координат ( b = 0) под углом α = 45◦ ê положительному направлению оси Ox (k = tg α = 1), то есть является биссектрисой первого и третьего координатных углов (см. рис. 8).
6.Пусть k = −1, b = 0, то есть уравнение этой прямой имеет вид y = −x.
Эта прямая проходит через начало координат ( b = 0) под углом α = 135◦ к положительному направлению оси Ox (k = tg α = −1), òî åñòü
является биссектрисой второго и четвертого координатных углов (см. рис. 9).
Ðèñ. 4. |
Ðèñ. 5. |
Ðèñ. 6. |
Ðèñ. 7. |
7
Ðèñ. 8. |
Ðèñ. 9. |
|
Если прямая с угловым коэффициентом k проходит через точку (x1, y1) то ее уравнение можно записать так:
y − y1 = k(x − x1)
уравнение пучка прямых .
1.1.4.Тангенс угла между двумя прямыми на плоскости. Условия параллельности и перпендикулярности прямых.
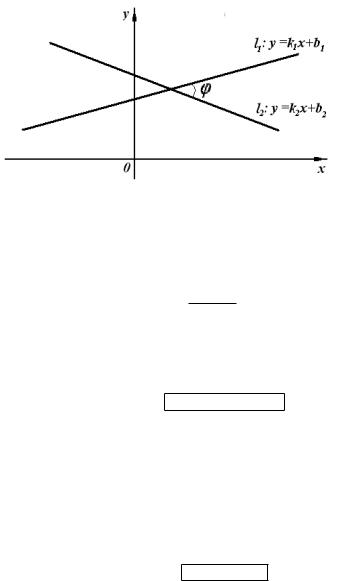
Пусть прямые l1 è l2 заданы уравнениями вида (5):
l1 : y = k1x + b1, l2 : y = k2x + b2.
Тогда тангенс угла ϕ (0 6 ϕ 6 90◦) между этими прямыми (см. рис. найти по формуле
tg ϕ = |
|
1 + k1k2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ðèñ. 10.
10) можно
(6)
8
Çíàÿ tg ϕ, с помощью таблиц, калькуляторов и т.п. можно найти сам угол
ϕ.
Выведем условие параллельности l1 k l2 и перпендикулярности l1 l2 ïðÿ- ìûõ l1 è l2.
Пусть l1 k l2. Тогда ϕ = 0, tg ϕ = 0, и, согласно формуле (6),
k1 − k2
= 0
1 + k1k2
èk1 = k2. При этом возможны 2 случая. Если k1 = k2 è b1 = b2, то прямые l1
èl2 совпадают. Если k1 = k2, íî b1 6= b2, то прямые l1 è l2 строго параллельны.
Обратное тоже верно. Итак,
k1 = k2, b1 6= b2
условие параллельности прямых l1 è l2.
Пусть l1 l2. Тогда ϕ = 90◦, è tg ϕ не существует. Это означает, согласно формуле (6), что знаменатель дроби в правой части (6) равен нулю:
1+ k1k2 = 0,
èk1 · k2 = −1. Обратное тоже верно: если k1 · k2 = −1, òî l1 l2. Èòàê,
k1 · k2 = −1
условие перпендикулярности прямых l1 è l2.
1.2. Лекция 2.
1.2.1. Матрицы и их основные виды.
Одним из основных понятий линейной алгебры является понятие матрицы.
Определение 2. Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются е¼ элементами.
9
Матрицы обозначаются: A, B, C. Иногда дополнительно указывается раз-
A , B и т.д. В общем виде матрица записывается
m×n m×n
|
a11 |
a12 |
... |
a1n |
|
A = |
a21 |
a22 |
... |
a2n |
|
|
m2 |
|
mn |
||
m1 |
... |
||||
a... |
a... |
... |
a... |
|
|
|
|
|
|
|
|
, ãäå
или, сокращ¼нно A = aij i = 1, . . . , m номер строки, j = 1, . . . , n
номер столбца, aij элемент, стоящий на пересечении i-ой строки и j-ого столбца.
Пример 3. Матрица
|
|
3 |
2 |
A = |
|
−1 |
0 |
|
1 |
4 |
имеет размер 3×2. Укажем несколько е¼ элементов: a21 = −1, a32 = 4, a11 = 3.
Определение 4. Две матрицы называются равными, если они одинакового размера и все их соответствующие элементы совпадают.
Определение 5. Матрица называется квадратной n-ого порядка, если число е¼ строк равно числу столбцов и равно n.
Пример 6. Матрица |
|
|
B = |
3 |
8 |
0 |
−7 |
является квадратной матрицей второго порядка.
Определение 7. Элементы матрицы aij, у которых i = j, называются диагональными и они образуют главную диагональ матрицы.
Пример 8. В матрице A из примера 3 главную диагональ образуют элементы a11 = 3 è a22 = 0.
Определение 9. Квадратная матрица, у которой все недиагональные элементы равны нулю, называется диагональной.
Пример 10. Матрица |
|
|
C = |
3 |
0 |
0 |
−2 |
является диагональной.
Определение 11. Диагональная матрица n-ого порядка называется единичной матрицей n-ого порядка и обозначается E, если все е¼ диагональные элементы равны единице.
Пример 12. Матрица |
0 |
1 |
0 |
E = |
|||
|
1 |
0 |
0 |
|
0 |
0 |
1 |
является единичной матрицей 3-го порядка. |
|
||
10
Определение 13. Матрица любого размера называется нулевой, если все е¼ элементы равны нулю.
Определение 14. Матрица размера m×1 называется матрицей-столбцом.
Определение 15. Матрица размера 1 × n называется матрицей-строкой.
Пример 16. |
0 |
||
A = |
|||
|
|
1 |
|
|
4 |
||
|
|
||
|
|
2 |
|
|
|
||
матрица-столбец, |
B = 1 3 −1 |
матрица-строка. |
1.2.2. Действия над матрицами.
Определение 17. Произведением числа λ на матрицу A размера m × n
называется матрица B = λ · A, размера m × n, элементы которой bij = λ · aij,
i = 1 . . . m, j = 1 . . . n. |
|
|
|
|
|
Пример 18. |
|
|
|
|
|
2 |
1 6 |
2 = |
−2 −12 |
−4 . |
|
− · |
−3 0 |
1 |
6 0 |
−2 |
Определение 19. Суммой (разностью) двух матриц A и B одного размера m Ч n называется матрица C = A ± B того же размера, элементы которой
cij = aij ± bij, i = 1 . . . m, j = 1 . . . n. |
|
|
|
|
|
||
Пример 20. |
|
2 |
−3 |
= |
−4 |
0 |
. |
−2 −3 |
|||||||
1 |
6 |
−3 5 |
|
4 |
1 |
|
|
8 |
1 − 7 |
0 1 |
1 |
|
|||
Произведение двух матриц A и B определено тогда и только тогда, когда число столбцов первого множителя A равно числу строк второго множителя
B.
Определение 21. Произведением двух матриц A è B называется мат-
m×k k×n
ðèöà C = A · B, элемент которой cij равен сумме произведений элементов i-
m×n
ой строки матрицы A на соответствующие элементы j-ого столбца матрицы B, i = 1 . . . m, j = 1 . . . n.
Пример 22. Матрицу
A = |
−3 |
4 |
7 |
|
4 |
−1 |
0 |
невозможно умножить на матрицу
5 6 B = 4 0 ,
11
так как число столбцов матрицы A равно 3 и не совпадает с числом строк матрицы B.
Пример 23. Матрицу |
|
4 |
5 |
|
A = |
||||
|
|
1 |
−2 |
|
можно умножить на матрицу |
−1 |
0 |
|
|
2 |
3 |
6 |
|
|
B = |
1 |
0 |
−1 , |
|
так как число столбцов матрицы A равно 2 и совпадает с числом строк матрицы B. Произведение A · B имеет размеры 3 × 3. Число строк произведения равно числу строк первого множителя A, число столбцов произведения равно числу столбцов второго множителя B. Найд¼м произведение
|
|
|
|
|
· |
|
|
1 |
−2 |
|
1 |
0 |
1 |
|
|
|
|
|
|
|||
|
|
|
|
A |
B = |
|
|
1 |
0 |
|
|
· 2 |
3 |
6 |
|
|
|
|
|
|
||
|
|
|
|
|
|
4 |
5 |
|
|
|
− |
|
= |
|
|
|
|
|
||||
|
|
·4 1 + 5 2 |
|
|
|
− |
|
|
|
|
|
= |
14 15 26 |
|
|
|||||||
= |
4 0 + 5 3 |
|
4 (−1) + 5 · 6 |
. |
||||||||||||||||||
|
1 |
1 + (−2) · 2 |
1 · 0 + (−2) |
· 3 1 · |
(−1) + (−2) |
· 6 |
|
|
−3 |
−6 |
−13 |
|
||||||||||
|
(−1)· |
· 1 + ·0 · 2 |
(−1)· |
· 0 + ·0 · 3 (−1)· |
· (−1) + 0 · 6 −1 |
0 |
1 |
|
|
|||||||||||||
Пример 24. Матрицу
1 4 A = 3 5
можно умножить на матрицу
B = |
−1 |
0 |
1 |
−7 |
, |
|
2 |
3 |
6 |
1 |
|
так как число столбцов матрицы A равно 2 и совпадает с числом строк матрицы B. Произведение A · B имеет размеры 2 Ч 4. Число строк произведения равно числу строк первого множителя A, число столбцов произведения равно числу столбцов второго множителя B. Найд¼м произведение
|
|
· |
|
3 |
5 · |
2 |
3 |
6 |
1 |
|
|
|
3 ·· |
A |
|
B = 1 |
4 |
−1 0 |
1 |
−7 |
|
= |
|
||
(−1) + 5 · 2 |
3 · 0 + 5 · 3 |
3 · 1 + 5 · 6 |
3 · (−7) + 5 · 1 |
|||||||||
= 1 (−1) + 4 |
· 2 |
1 · 0 + 4 · 3 |
1 |
· 1 + 4 · 6 |
1 |
· |
(−7) + 4 |
· 1 = |
||||
= |
7 |
12 |
25 |
−3 |
. |
|
7 |
15 |
33 |
−16 |
|
Произведения AB и BA не обязаны совпадать, даже если они оба определены и имеют один размер.
Замечание 26. Единичная матрица E обладает тем свойством, что если имеет смысл выражение EX (XE), то
EX = X (соответственно, XE = X).
12

Определение 27. Степенью Am (m = 2, 3, 4, . . .) квадратной матрицы A называется произведение m матриц, равных A:
Am = A · A · . . . · A .
| {z } m экземпляров
Матрица Am является квадратной матрицей того же порядка, что и матрица
.
Пример 28. Пусть
|
|
0 |
5 |
|
|
|
|
|
|
тогда |
|
A = −3 |
4 |
, |
|
|
|
|
|
4 · −3 |
4 −3·· 0 + 4·· (−3) (−3) · 5 + 4 · 4 −12 |
1 |
|
||||||
−3 |
|||||||||
A2 = 0 |
5 0 |
5 = 0 0 + 5 (−3) |
0 |
· 5 + 5 · 4 |
= −15 |
20 . |
|
||
Определение 29. Матрица A0 называется транспонированной к матрице A, если е¼ строки совпадают со столбцами матрицы A, а столбцы совпадают со строками матрицы A.
Если матрица A имеет размер m Ч n, то транспонированная матрица A0 имеет размер n Ч m.
Пример 30. Транспонируем матрицу
27
A = 0 −1 .
3×2 3 4
Поменяем строки и столбцы матрицы A местами и получим транспонированную матрицу
A0 = |
2 |
0 |
3 |
. |
2×3 |
7 |
−1 |
4 |
|
1.3. Лекция 3.
1.3.1. Определители квадратных матриц.
Каждой квадратной матрице A можно поставить в соответствие определенное число, называемое определителем (детерминантом) этой матрицы и обо-
значающееся символом = A . Понятие определителя является одним из
ключевых понятий линейной алгебры. Выясним, по какому закону квадратной матрице ставится в соответствие ее определитель. Сначала рассмотрим квадратные матрицы малых порядков: первого, второго и третьего.
Определение 31. |
Определителем первого порядка матрицы a11 |
называ- |
|
|
|
ется число = a11 = a11.
Определение 32. Определителем второго порядка матрицы
a11 a12 a21 a22
называется число
= |
a11 |
a12 |
|
= a11 · a22 − a12 · a21. |
(7) |
a21 |
a22 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
13
Пример 33.
−3 |
7 |
= |
− |
5 |
· |
7 |
− |
1 |
· − |
− |
− |
|
−5 |
1 |
|
|
|
( 3) = |
|
35 + 3 = 32. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение 34. Определителем третьего порядка матрицы
a11 a12 a13
a21 a22 a23 a31 a32 a33
называется число
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
a11 |
a12 |
a13 |
= a11 · (−1) |
|
|
|
· |
a32 |
a33 |
+ |
|
||||||
|
a21 |
a22 |
a23 |
1+1 |
|
|||||||||||||||
|
|
|
a |
a |
a |
|
|
|
|
a22 |
a23 |
|
|
|
||||||
|
|
31 |
32 |
|
33 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+a12 |
|
|
|
a21 |
a23 |
|
|
|
|
· |
|
a21 |
a22 |
. |
|
|
(8) |
|||
· (−1)1+2 · a31 |
a33 |
+ a13 · (−1)1+3 |
a31 |
a32 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 35. Вычислим определитель
3 −1 2
−2 7 4
1 |
0 5 |
. По формулам (8) è (7) находим:
|
3 |
−1 |
2 |
|
|
· |
− |
|
· |
7 |
4 |
|
|
− |
|
· − |
· |
|
|
2 |
4 |
|
|
· |
− |
|
· |
|
|
2 |
7 |
|
|
1 |
0 |
5 |
= 3 |
1)1+1 |
|
|
+( |
1) |
− |
|
|
+2 |
1)1+3 |
− |
|
|
= |
||||||||||||||||
|
2 |
7 |
4 |
|
( |
|
|
|
|
|
|
( 1)1+2 |
|
|
|
|
|
( |
|
|
|
|
|
|
|||||||||
|
− |
|
|
|
|
|
|
|
|
0 |
5 |
|
|
|
|
|
|
|
1 |
5 |
|
|
|
|
|
|
|
1 |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 3 · (7 · 5 − 4 · 0) + (−2 · 5 − 4 · 1) + 2 · (−2 · 0 − 7 · 1) = 105 − 14 − 14 = 77.
Перейдем к общему случаю. Пусть A квадратная матрица n-ого порядка.
квадратной матрицы A n- ого порядка называется определитель матрицы (n−1)-ого порядка, полученной из матрицы A вычеркиванием i-ой строки и j-ого столбца.
Пример 37. Минором элемента a23 матрицы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
a11 |
a12 |
a13 |
|
|
|
|
|
|
|
|
a21 |
a22 |
a23 |
|
|
|
||
третьего порядка будет |
|
|
a31 |
a32 |
a33 |
|
|
|
|||
|
|
M23 |
|
a11 |
a12 |
= a11a32 − a12a31. |
|
|
|||
|
|
= a31 |
a32 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Определение 38. Алгебраическим |
дополнением |
Aij |
элемента |
aij квадрат- |
|||||||
|
|
|
|
|
|
|
|
|
|
||
|
матрицы |
|
|
|
|
|
|
|
|
i+j: |
|
íîé |
= (−1) |
i+jn-ого порядка называется минор Mij, взятый со знаком (−1) |
|||||||||
Aij |
Mij. Другими словами, Aij |
= Mij, åñëè i + j четно и Aij = |
|||||||||
−Mij, åñëè i + j нечетно.
14
Пример 39. A12 = (−1)1+2M12 = −M12; A31 = (−1)3+1M31 = M31.
Определение 40. Определитель (детерминант) произвольной квадратной матрицы есть сумма произведений элементов любой строки (столбца) на их алгебраические дополнения:
|
n |
|
Xj |
|A| = ai1Ai1 + ai2Ai2 + . . . + ainAin = aijAij |
|
|
=1 |
(разложение определителя по элементам |
i-ой строки ); |
|
n |
|
Xi |
|A| = a1jA1j + a2jA2j + . . . + anjAnj = aijAij |
|
|
=1 |
(разложение определителя по элементам |
j-ого столбца ). |
1.3.2. Свойства определителей.
1. Определитель матрицы не изменится, если матрицу транспонировать.
Пример 41. |
3 |
2 |
|
|
|
|
7 |
2 |
|
||
|
= |
|
|||||||||
|
|
4 |
−7 |
|
|
4 |
3 |
. |
|
||
|
|
|
|
− |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.При умножении строки (или столбца) определителя на число c определитель увеличится в c ðàç.
Пример 42. |
|
3 |
5· |
4 |
32· 7 = 3 · |
5 2 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
4 |
7 |
|
|
|||
Пример 43. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
3 |
= 4 |
· |
|
3 |
|
. |
|||||||
|
|
|
8 |
|
−1 |
|
|
|
2 |
|
−1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. При перестановке двух строк (столбцов) определитель изменит знак.
Пример 44. |
4 3 |
0 |
= |
|
8 −1 |
7 |
. |
|
|
|
|||||||
|
8 |
−1 |
7 |
|
− |
4 3 |
0 |
|
|
1 2 |
6 |
|
1 2 6 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.Если определитель содержит нулевую строку (столбец), то он равен нулю.
5.Если определитель содержит две равные строки (столбца) или пропорциональные строки (столбцы), то он равен нулю.
Пример 45. |
|
8 |
|
|
|
−2 7 |
4 |
−1 |
0 |
= 0, |
−4 |
1 |
6 |
|
|
|
|
|
|
|
|
|
так как первый и второй столбец определителя пропорциональны.
6.Определитель не изменится, если в н¼м к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца).
15
Пример 46. |
|
4 |
−1 |
0 |
= |
4 −1 |
0 |
, |
|
|
|||||||||
|
|
9 |
−3 |
4 |
|
9 |
−3 |
4 |
|
|
4 |
7 |
6 |
|
0 |
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
так как последний определитель получен из первого прибавлением к третьей строке второй.
7.Определитель матрицы, все элементы над (под) главной диагональю которой равны нулю, равен произведению диагональных элементов:
|
a11 |
a12 ... |
||
0 |
a22 ... |
|||
... ... ... |
||||
|
|
|
|
|
|
0 |
0 ... |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
0 ... |
|||
a21 |
a22 ... |
|||
... |
... ... |
|||
|
|
|
|
|
a |
a |
n2 |
... |
|
|
n1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a1n
a2n
... = a11
ann
... = a11
ann
· a22 · . . . · ann;
· a22 · . . . · ann.
В частности, определитель диагональной матрицы равен произведению диагональных элементов:
|
|
|
|
|
|
|
|
|
a11 |
0 ... |
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
a22 ... |
0 |
|
= a11 · a22 · . . . · ann. |
|
|
... |
... ... |
... |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 47. |
|
0 |
0 ... |
ann |
|
|
|
9 |
0 0 |
|
|
|
|
|
|
|
|
|
|
|
−4 |
7 |
6 |
= 9 |
· |
( |
− |
5) |
· |
6 = |
− |
270. |
4 |
−5 |
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 48. |
1 0 |
0 |
|
|
|
|
|
0 |
3 |
0 |
= 1 · 3 · (−4) = −12. |
0 |
0 |
−4 |
|
|
|
|
|
|
|
|
|
1.3.3. Ранг матрицы и его вычисление.
Понятие ранга матрицы играет важную роль при решении ряда математи- ческих и прикладных (в том числе экономических) задач.
Определение 49. Подматрицей матрицы A называется матрица, полученная из матрицы A вычеркиванием некоторых строк и/или столбцов.
Определение 50. Минорами k-ого порядка матрицы A называются определители ее квадратных подматриц k-ого порядка.
Например, у матрицы A размера 3 Ч 5 существуют миноры первого, второго и третьего порядков. У матрицы A размера mЧn существуют миноры порядка k 6 min{m, n}.
Определение 51. Рангом матрицы A называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначение: r(A).
16
Ранг матрицы обладает следующими свойствами:
1)Åñëè m × n размер матрицы A, òî r(A) 6 min{m, n}.
2)Åñëè A квадратная матрица n-ого порядка, то r(A) = n тогда и только тогда, когда |A| 6= 0.
3)r(A) = 0 тогда и только тогда матрица A нулевая, то есть все ее элементы равны нулю.
Пример 52. Пользуясь определением 51, вычислим ранг матрицы
|
|
0 |
9 |
1 |
7 |
|
A = |
|
0 |
0 |
−5 |
9 . |
|
|
0 |
3 |
4 |
5 |
||
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
Матрица A имеет размер 4 Ч 4, поэтому r(A) 6 4. Но |A| = 0, так как матрица A содержит нулевой столбец, значит, r(A) 6 3. При этом матрица A содержит ненулевой минор 3-его порядка
|
|
9 1 7 |
|
|
|
|
0 |
−5 |
9 |
= 9 |
· |
( |
− |
5) |
· |
1 = |
− |
45 |
|
, |
0 |
0 |
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поэтому r(A) = 3.
Но в большинстве случаев вычисление ранга матрицы перебором миноров трудоемко. Более удобно вычислять ранг матрицы, проводя над ней следующие
элементарные преобразования :
1)изменение порядка строк (столбцов) матрицы;
2)вычеркивание нулевой строки (столбца) матрицы;
3)умножение всех элементов строк (столбцов) матрицы на ненулевое число;
4)прибавление к элементами строки (столбца) матрицы соответствующих элементов другой строки (столбца);
5)транспонирование матрицы.
Теорема 53. Ранг матрицы не меняется при элементарных преобразованиях.
С помощью элементарных преобразований матрица приводится к ступенча- тому виду.
Определение 54. Cтупенчатой матрицей называется матрица A âèäà
|
0 |
a22 |
· · · |
a2r |
· · · |
a2k , |
|||
a11 |
a12 |
|
a1r |
|
a1k |
|
|||
. |
0. . . . |
. .0. . . |
.·.·.·. . |
.a. |
rr. . . . |
·.·.·. . |
.a. |
rk. . |
|
|
|
|
· · · |
|
· · · |
|
|
||
|
|
|
|
|
|
|
|
||
ãäå a11, a22, ... ,arr 6= 0. |
|
|
|
|
|
|
|
|
|
17
Ступенчатая матрица содержит ненулевой минор r-о порядка:
a11 a12 · · · a1r
. 0. . . . .a.22. . . .·.·.·. . |
.a. |
2.r. |
= a11 · a22 · ... · arr 6= 0, |
|
|
|
|
|
|
|
|
0 |
0 · · · arr |
òàê êàê âñå aii 6= 0 (i = 1, 2, . . . , r), поэтому справедлива
Теорема 55. Ранг ступенчатой матрицы равен r числу ее строк.
Пример 56. Вычислим ранг матрицы
|
|
−3 |
8 |
5 |
|
|
A = |
1 |
−10 |
2 . |
|||
|
|
7 |
4 |
19 |
||
|
|
−2 |
−2 |
7 |
|
|
|
− |
|
|
|
|
|
Выполним необходимые элементарные преобразования. Если это возможно,
удобно переставить строки и/или столбцы так, чтобы a11 = ±1. Поменяем местами первую и вторую строки:
1 −10 |
2 |
3 |
−8 |
5 |
|
|
||||||||
|
3 |
8 |
5 |
|
|
1 |
10 |
2 |
|
|
||||
|
7 |
4 |
19 |
|
7 |
44 |
|
11 |
|
|||||
|
|
|
− |
|
|
|
|
|
|
− |
|
|
|
|
|
4 |
|
2 |
7 |
|
|
4 |
2 |
7 |
|
|
|||
− |
|
|
|
|
|
− |
|
− |
− |
|
|
|||
Обнулим все элементы первого столбца, кроме первого элемента. Для этого последовательно умножим первую строку на (−3), (−4) и 7 и прибавим ко второй, третьей и четвертой строке, соответственно:
3 |
−8 |
5 |
|
0 |
38 |
−1 |
|
||||||
|
1 |
10 |
2 |
|
|
1 |
−10 |
2 |
|
|
|||
|
7 |
−44 |
|
11 |
0 |
|
114 |
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
4 |
2 |
7 |
|
|
0 |
38 |
1 |
|
|
|||
− |
|
− |
− |
|
|
|
− |
|
|
|
|||
Обнулим все элементы второго столбца, кроме первых двух элементов. Для этого последовательно умножим вторую строку на (−1) и 3, затем прибавим к третьей и четвертой строке, соответственно:
0 |
38 |
−1 |
0 38 −1 |
|
|||||||
|
1 |
−10 |
2 |
|
|
1 |
−10 |
2 |
|
|
|
0 |
|
114 |
3 |
0 |
0 |
0 |
|
||||
|
|
|
|
− |
|
|
|
|
|
|
|
|
0 |
38 |
1 |
|
|
0 |
0 |
0 |
|
|
|
|
|
− |
|
|
|
|
|
|
|
||
Вычеркнем нулевые строки (третью и четвертую):
0 38 −1 |
1 |
−10 2 . |
||||
|
1 |
−10 |
2 |
|
0 |
38 1 |
|
0 |
0 |
0 |
|||
0 |
0 |
0 |
|
− |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученная матрица является ступенчатой. Число ее строк равняется рангу исходной матрицы: r(A) = 2.
18
1.4. Лекция 4.
1.4.1. Системы линейных уравнений: основные понятия.
Определение 57. Системой из m линейных уравнений с
(неизвестными) называется система вида
a21x1 |
+ a22x2 |
+ . . . |
+a2nxn = b2 |
, |
a11x1 |
+ a12x2 |
+ . . . |
+a1nxn = b1 |
, |
|
|
|
|
|
. . . . . |
. . . . . . . . . |
. . . . . . . |
. . . . . . . . . . . . . |
. |
|
|
|
|
|
|
|
|
|
|
am1x1 + am2x2 + . . . |
+amnxn = bm, |
|||
|
|
|
|
|
n переменными
(9)
ãäå xj (j = 1, 2, . . . , n) неизвестные, а aij, bi (i = 1, 2, . . . , m, j = 1, 2, . . . , n) произвольные числа.
Определение 58. Решением системы (9) называется совокупность n чисел (x1 = k1, x2 = k2, ... ,xn = kn), при подстановке которых каждое уравнение системы обращается в верное равенство.
Определение 59. Две системы уравнений называются равносильными (эквивалентными ), если они имеют одно и то же множество решений.
Определение 60. Система (9) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Определение 61. Система (9) называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
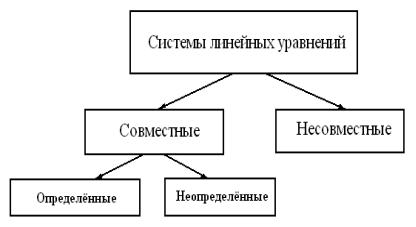
Таким образом, имеет место следующая схема:
Ðèñ. 11.
С системой (9) можно связать три матрицы:
A = |
a11 |
a12 |
· · · |
a1n |
матрица системы , |
|||
a. . |
21. . . . |
a. . |
22. . . . |
·.·.·. . . |
a. . |
2.n. |
||
|
a |
a |
|
|
a |
|
|
|
|
|
1m |
m2 |
|
mn |
|
||
|
|
|
|
|
· · · |
|
|
|
19
x1
|
X = |
x2 |
матрица-столбец переменных , |
|
|
|
|
|
b1 |
x. .m. |
|
B = |
b2 |
матрица-столбец свободных коэффициентов . |
|
|
b. . . |
|
|
|
m |
|
|
|
|
|
|
Запишем систему (9) в матричной форме. Для этого сначала перемножим матрицы A è X:
AX = |
a21 |
a22 |
· · · |
a2n |
x2 |
= |
a21x1 |
+ a22x2 |
+ . . . |
+a2nxn |
, |
|
|
a11 |
a12 |
|
a1n |
x1 |
|
|
a11x1 |
+ a12x2 |
+ . . . |
+a1nxn |
|
|
a. . . . . . a. . . . . .·.·.·. . .a. . . . x. . . |
|
a. . . .x. . .+. .a. . . .x. . .+. ....... . .+. .a. . . .x. . |
|
||||||||
|
1m m2 |
· · · |
mn m |
|
m1 1 |
m2 2 |
mn n |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
то есть в результате получается матрица, содержащая левые части уравнений системы (9). Так как левые части системы должны совпадать с соответствую-
щими правыми частями, то эта матрица и матрица B должны быть равными:
AX = B. |
(10) |
Формула (10) и является матричной формой записи системы (9). Заметим, что линейное уравнение с одной переменной, изучаемое в школьном курсе, тоже можно записать в виде (10). Разница лишь в том, что если рассматривать
одно линейное уравнение с одной переменной, то под A, X и B в системе (10) надо понимать числа, а если рассматривать систему уравнений, то A, X и B в системе (10) будут означать матрицы.
1.4.2. Обратная матрица и ее нахождение. −1 такое, Для всякого числа a 6= 0 можно определить обратное ему число a
÷òî a · a−1 = 1. Аналогично вводится понятие матрицы, обратной данной.
Определение 62. Пусть A квадратная матрица. Матрицей, обратной к матрице A, называется квадратная матрица того же порядка A−1 такая, что
A · A−1 = A−1 · A = E.
Ниже приведены условие существования обратной матрицы и формула для
ååнахождения.
Определение 63. Квадратная матрица называется невырожденной, åñëè
ååопределитель не равен нулю.
Теорема 64. Если A квадратная матрица, то обратная матрица A−1 существует тогда и только тогда, когда матрица A является невырожденной.
Теорема 65.
ратная матрица формуле
Пусть A невырожденная квадратная матрица. Тогда об- A−1 определяется единственным образом и находится по
A−1 = |
1 |
A12 |
A22 |
... |
An2 |
, |
(11) |
||||
|
|
|
A11 |
A21 |
... |
An1 |
|
|
|||
|
|
A |
1n |
a |
2n |
... |
A |
nn |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
... ... ... ... |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
20
ãäå = |A|, Aij алгебраические дополнения к элементам матрицы A.
Замечание 66. Матрица из алгебраических дополнений, стоящая в правой части формулы (11) называется матрицей, присоединенной к матрице A.
Пример 67. Докажем, что для матрицы
|
2 |
−3 |
4 |
A = |
1 |
5 |
−2 |
|
4 |
1 |
−5 |
существует обратная матрица A−1 и найдем ее. Имеем:
2 −3 4
= |A| = 1 5 −2 =
4 1 −5
= 2 · (−1)1+1 · |
1 |
−5 |
+ (−3) · (−1)1+2 |
· |
4 |
−5 |
+ 4 · (−1)1+3 |
· |
4 |
1 |
= |
||||||||
|
|
5 |
− |
2 |
|
|
|
|
1 |
− |
2 |
|
|
|
|
1 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2·(5·(−5)−(−2)·1)+3·(1·(−5)−(−2)·4)+4·(1·1−5·4) = −46+9−76 = −113.
6= 0, значит, по теореме 64, существует обратная матрица A−1. Ïî ôîð- ìóëå (11)
|
|
|
|
|
|
|
|
A−1 = |
1 |
A11 |
A21 |
A31 |
|
|
|
A12 |
A22 |
A32 |
, |
||||
|
|||||||
|
|
A13 |
A23 |
A33 |
|
ãäå Aij (i, j = 1, 2, 3) алгебраические дополнения к элементам матрицы A. Найдем Aij:
A11 = (−1)1+1 5 −2 = 5 · (−5) − (−2) · 1 = −23;
1 −5
A21 = (−1)2+1 −3 4 = −((−3) · (−5) − 4 · 1) = −11;
1 −5
A31 = (−1)3+1 −3 4 = (−3) · (−2) − 4 · 5 = −14;
5 −2
A12 = (−1)1+2 1 −2 = −(1 · (−5) − (−2) · 4) = −3;
4 −5
A22 = (−1)2+2 2 4 = 2 · (−5) − 4 · 4 = −26;
4 −5
A32 = (−1)3+2 2 4 = −(2 · (−2) − 4 · 1) = 8;
1 −2
A13 = (−1)1+3 1 5 = 1 · 1 − 5 · 4 = −19;
4 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A23 |
= ( |
− |
1)2+3 |
2 −3 |
|
= |
(2 |
1 |
− |
( |
− |
3) |
· |
4) = |
14; |
|
|
|
4 1 |
|
− · |
|
|
|
|
− |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A33 |
= ( |
− |
1)3+3 |
2 |
−3 |
|
= 2 |
· |
5 |
− |
( |
− |
3) |
· |
1 = 13. |
|
|
|
1 |
5 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом,
|
|
|
|
|
|
|
|
|
23 |
11 |
14 |
|
|
|
|
||||
|
1 |
|
−23 |
−11 |
−14 |
|
|
|
113 |
|
113 |
|
113 |
|
|
|
|
||
|
|
|
|
|
3 |
|
26 |
|
|
8 |
|
|
|
|
|||||
A−1 |
= |
|
|
3 |
26 |
8 |
|
= |
|
|
|
|
|
. |
|||||
|
|
|
|
− |
− |
|
|
113 |
113 |
|
|
113 |
|
|
|||||
|
−113 |
−19 |
−14 |
13 |
|
|
|
113 |
113 |
− |
113 |
|
|
||||||
|
|
|
19 |
14 |
13 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.4.3. Решение систем линейных уравнений методом обратной матрицы.
Пусть в системе линейных уравнений число уравнений совпадает с числом неизвестных (m = n). Предположим, что матрица A данной системы невырожденна. Тогда, по теореме 64 существует обратная матрица A−1. Умножим обе части равенства (10) слева на A−1, затем проведем преобразования:
A−1 · A · X = A−1 · B, E · X = A−1 · B, X = A−1 · B.
Таким образом, верна
Теорема 68. Пусть задана система линейных уравнений, в которой число уравнений совпадает с числом неизвестных, причем матрица системы является невырожденной. Тогда система имеет единственное решение, которое можно найти по формуле
X = A−1 B. |
(12) |
Пример 69. Решим методом обратной матрицы систему линейных уравне-
íèé |
|
|
x1 |
+ 5x2 |
|
2x3 |
= 15, |
(13) |
||
|
|
|
|
|||||||
|
|
|
|
2x1 |
− |
3x2 |
+ 4x3 |
= −4, |
|
|
|
|
|
|
|
|
− |
|
|
|
|
Выпишем связанные с |
4x1 + x2 |
|
5x3 = 19. |
|
||||||
|
|
|
|
− |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
A = |
1 |
системой матрицы: |
|
15 . |
||||||
5 −2 |
, X = x2 , B = |
|||||||||
|
2 |
−3 4 |
|
|
|
|
x1 |
−4 |
||
|
4 |
1 −5 |
|
|
x3 |
19 |
||||
Так как = |A| = −113 6= 0 (см. пример 67), то система (13) имеет единственное решение. По формуле (12)
X = A−1 B,
и, подставляя в последнюю формулу матрицу A−1, найденную в примере 67, получим:
X = 113 |
−3 |
−26 |
8 |
|
15 |
= |
||
|
|
1 |
−23 |
−11 |
−14 |
|
−4 |
|
|
|
|
−19 |
−14 |
|
|
|
|
|
− |
|
13 |
19 |
||||
|
|
|
|
|
|
|
|
|
(−23) · (−4) + (−11) · 15 + (−14) · 19
1 = −113 (−3) · (−4) + (−26) · 15 + 8 · 19 =
(−19) · (−4) + (−14) · 15 + 13 · 19
|
|
|
|
1 |
|
|
92 |
− 165 |
− 266 |
|
|
|
3 |
|
|
|
||
|
|
= |
|
|
|
12 |
− 390 |
+ 162 |
|
= |
|
2 |
|
. |
|
|||
Таким образом, |
|
− |
113 |
|
||||||||||||||
|
, |
|
|
|
− |
|
|
|
− |
|
|
|||||||
|
x1 |
= 3 x2 |
= 2 |
, |
x3 |
= −1 |
решение исходной системы. |
|
||||||||||
22
1.4.4. Решение систем линейных уравнений методом Крамера.
Теорема 70. Пусть задана система линейных уравнений, в которой число уравнений совпадает с числом неизвестных (m = n), причем матрица A си-
стемы является невырожденной. Тогда система имеет единственное решение (x1, x2, . . . , xn), которое можно найти по следующим формулам Крамера:
x1 = |
|
1 |
, x2 = |
2 |
, . . . , xn = |
n |
. |
(14) |
|
|
|
|
|||||
Здесь = |A|, а i (i = |
1, 2, . . . , n) определитель матрицы, полученной из |
|||||||
матрицы A заменой i-ого столбца на столбец свободных коэффициентов |
B. |
|||||||
Пример 71. Решим по формулам Крамера систему линейных уравнений
2x1 − 3x2 + 4x3 = −4,
x1 + 5x2 − 2x3 = 15,
4x1 + x2 − 5x3 = 19
(система та же, что и в задаче 69). Запишем матрицы
A = |
1 |
5 |
−2 |
, B = |
15 |
. |
|
|
2 |
−3 |
4 |
|
|
−4 |
|
|
4 |
1 |
−5 |
|
19 |
|
|
Òàê êàê = |A| = −113 6= 0 (см. пример 67), то данная система имеет единственное решение. По формуле (14)
x1 = |
1 |
, |
x2 = |
|
2 |
, |
|
x3 = |
3 |
. |
(15) |
|
|
|
|
||||||||
Имеем: |
|
|
−4 |
−3 |
4 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
1 = 15 5 −2 =
|
|
|
|
|
|
|
|
|
|
|
1 |
|
−5 |
|
|
|
|
|
|
|
|
|
|
|
− |
|
− |
|
1 |
−5 |
19 |
|
|
−5 |
− |
19 1 |
|
||||||||||
= ( |
4)( |
1)1+1 |
− − |
1)1+2 |
19 |
= |
|||||||||||||||||
|
|
|
5 |
− |
2 |
|
+ ( 3)( |
|
15 |
− |
2 |
|
+ 4( 1)1+3 |
|
15 |
5 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −4(−25 + 2) + 3(−75 + 38) + 4(15 − 95) = 92 − 111 − 320 = −339;
2 −4 4
2 = 1 15 −2 =
4 19 −5
= 2 · (−1)1+1 |
19 |
−5 |
+ (−4) · (−1)1+2 |
4 |
−5 |
+ 4 · (−1)1+3 |
4 |
19 |
= |
||||||||
|
|
15 |
− |
2 |
|
|
|
1 |
− |
2 |
|
|
|
1 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 · (−75 + 38) + 4 · (−5 + 8) + 4 · (19 − 60) = −74 + 12 − 164 = −226;
2 −3 −4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 = 1 5 |
|
|
15 |
= |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
· |
( |
− |
1)1+1 |
5 |
15 |
|
+ ( |
− |
3) |
· |
( |
41)1+2 |
|
1 |
15 |
+ ( |
4) |
( |
− |
1)1+3 |
1 |
5 |
|
= |
|
|
|
|
1 19 |
|
|
|
− |
4 19 |
|
− · |
|
|
4 1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23

= 2 · (95 − 15) + 3 · (19 − 60) − 4 · (1 − 20) = 160 − 123 + 76 = 113.
Подставляя |
|
1, 2 è 3 в формулу (15), получим: |
|
|
|
|
|
||||||||
x |
= |
|
−339 |
= 3, |
x |
= |
−226 |
= 2, |
x = |
113 |
= |
− |
1. |
||
|
− |
|
− |
|
|||||||||||
1 |
|
|
|
2 |
|
− |
113 |
|
3 |
113 |
|
|
|||
|
113 |
|
|
|
|
|
|
|
|||||||
Таким образом, x1 = 3, x2 = 2, x3 = −1 решение исходной системы.
1.5. Лекция 5.
1.5.1. Решение систем линейных уравнений методом Гаусса.
Метод Гаусса является одним из универсальных методов решения систем линейных уравнений. Метод позволяет решать, как определенные, так и неопределенные (имеющие больше одного решения) системы, а также определять системы, которые вообще не имеют решения.
Метод Гаусса состоит из двух этапов. На первом этапе (прямой ход метода Гаусса) с помощью элементарных преобразований исходная система приводится к равносильной системе, имеющей более простой (ступенчатый) вид. На втором этапе (обратный ход метода Гаусса) путем перемещения снизу вверх от последнего уравнения к первому и последовательного нахождения неизвестных находится решение получившейся системы.
Перейдем к основным понятиям, связанным с методом Гаусса. Система линейных уравнений имеет ступенчатый вид, если она представлена в следующей форме:
|
11 1 |
a22x2 |
+ . . . + a2rxr + . . . + a2nxn = b2 |
, |
|
|
a |
x + a12x2 |
+ . . . + a1rxr + . . . + a1nxn = b1 |
, |
, a22 |
, . . . , arr = 0. |
|
|
|
|
|
a11 |
||
. |
. . . . . . |
. . . . . . |
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arrxr + . . . + arnxn = br, |
|
|
|
(16) Элементарными преобразованиями системы называются следующие дей-
ствия:
1)изменение порядка уравнений или переменных;
2)вычеркивание уравнения, все коэффициенты в левой части, а также правая часть которого равны нулю;
3)умножение левой и правой частей одного из уравнений на ненулевое число;
4)прибавление к левой и правой частям одного из уравнений соответствующих частей другого уравнения;
Теорема 72. Исходная система и система, полученная из исходной в результате элементарных преобразований, равносильны.
Обычно элементарные преобразования проводят не над самой системой, а над ее расширенной матрицей. Расширенной матрицей Aр системы линейных
уравнений (54) называется матрица системы A, к которой справа приписан столбец свободных коэффициентов B:
Að = |
a21 |
a22 |
. . . a2n |
|
|
a11 |
a12 |
. . . |
a1n |
|
a. . . |
a. . . |
.. .. .. |
a. . . |
|
m1 |
m2 |
|
mn |
|
|
|
|
|
b1
b2
.
. . . bm
24
При этом вместо элементарных преобразований над системами будем проводить соответствущие элементарные преобразования над матрицами (см. пункт
1.3.3).
Применение метода Гаусса рассмотрим на примерах. Сначала рассмотрим случай, когда система имеет единственное решение.
Пример 73. Решим методом Гаусса систему линейных уравнений
2x1 − 3x2 + 4x3 = −4,
x1 + 5x2 − 2x3 = 15,
4x1 + x2 − 5x3 = 19
(система та же, что и в задачах |
69 è 71). |
Запишем расширенную матрицу |
|||||
системы: |
1 |
5 |
−2 |
|
15 |
. |
|
Að = |
|
||||||
|
|
2 |
−3 |
4 |
|
−4 |
|
|
4 |
1 |
−5 |
|
19 |
||
Выполним элементарные преобразования над матрицей. Если это возможно,
удобно переставить строки так, чтобы a11 = ±1. Поменяем местами первую и вторую строки:
1 |
5 |
−2 |
15 |
2 |
−3 4 |
−4 |
||
2 |
−3 4 |
−4 |
1 |
5 |
−2 |
15 |
|
|
4 |
1 |
−5 |
19 |
4 |
1 |
−5 |
19 |
|
Обнулим все элементы первого столбца, кроме первого элемента. Для этого последовательно умножим первую строку на (−2) è (−4), затем прибавим ее ко второй и третьей строке, соответственно:
|
0 |
−13 |
8 |
−34 |
|
|
1 |
5 |
−2 |
15 |
|
0 |
−19 |
3 |
−41 |
Обнулим последний элемент второго столбца. Для этого сначала последовательно умножим вторую строку на (−19), а третью на 13:
|
1 |
5 |
−2 |
15 |
|
0 |
247 |
152 |
646 |
||
|
0 |
−247 |
−39 |
−533 |
|
Прибавим к третьей строке вторую:
|
0 |
247 |
−152 |
646 |
. |
|
1 |
5 |
−2 |
15 |
|
0 |
0 |
−113 |
113 |
Полученная матрица является ступенчатой. Этой матрице, эквивалентной матрице Að, соответствует следующая система, равносильная исходной:
|
1 247x2 |
− |
152x3 |
= 646, |
(17) |
|
x + 5x2 |
− |
2x3 |
= 15, |
|
|
113x3 |
= 113. |
|
||
|
|
− |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
25

Двигаясь по системе (17) "снизу вверх", последовательно находим неизвестные x3, x2 è x1:
|
113 |
|
|
|
|
|
|
x3 = |
|
= |
−1; |
|
|
|
−113 |
|
||||
x2 = |
646 + 152 · (−1) |
= |
494 |
= 2; |
||
|
247 |
|||||
|
247 |
|
|
|
||
x1 = 15 − 5 · 2 + 2 · (−1) = 3.
Таким образом, x1 = 3, x2 = 2, x3 = −1 решение исходной системы.
Рассмотрим пример системы, у которой не будет решений. Пример 74. Решим методом Гаусса систему линейных уравнений
3x1 |
+ 2x2 |
+ x3 |
= 8, |
||||
− |
x1 |
− |
4x2 |
+ 3x3 |
= 1, |
||
|
− |
x1 |
− |
6x2 + 7x3 |
= 12. |
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Запишем расширенную матрицу системы:
Að = |
−3 |
2 |
1 |
8 |
. |
|
1 |
−4 |
3 |
1 |
|
|
−1 |
−6 |
7 |
12 |
Выполним элементарные преобразования. Обнулим все элементы первого столбца, кроме первого элемента. Для этого умножим первую строку на 3 и прибавим ко второй, а затем прибавим первую строку к третьей:
−3 |
2 1 |
8 |
0 |
−10 |
10 |
11 |
|
1 |
−4 |
3 |
1 |
1 |
−4 |
3 |
1 |
−1 |
−6 |
7 |
12 0 |
−10 |
10 |
13 |
|
Обнулим последний элемент второго столбца, для чего вычтем из третьей строки вторую:
|
1 |
−4 |
3 |
1 |
|
|
0 |
10 |
10 |
11 |
. |
0 |
−0 |
0 |
2 |
Последняя строка матрицы может быть записана как уравнение
0x1 + 0x2 + 0x3 = 2,
которое не имеет решений, так как при любых x1, x2 è x3 его левая часть равна нулю, а правая 2. Это означает, что исходная система не имеет решений.
Рассмотрим примеры систем линейных уравнений, которые имеют бесконеч- ное множество решений. Нам понадобится следующие определения.
Определение 75. Общим решением системы линейных уравнений называется совокупность всех решений этой системы.
Определение 76. Частным решением системы линейных уравнений называется произвольное решение этой системы.
26

Пример 77. С помощью метода Гаусса найдем общее и некоторое частное решение системы линейных уравнений
3x1 |
+ 2x2 |
+ x3 |
= 8, |
||||
− |
x1 |
− |
4x2 |
+ 3x3 |
= 1, |
||
|
− |
x1 |
− |
6x2 + 7x3 |
= 10 |
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
(сравните эту систему с системой из примера 74). Запишем расширенную матрицу системы:
Að = |
−3 |
2 |
1 |
8 |
. |
|
1 |
−4 |
3 |
1 |
|
|
−1 |
−6 |
7 |
10 |
Выполняя элементарные преобразования подобно тому, как это делалось в примере 74, получим:
−3 |
2 |
1 |
8 |
|
|
0 |
−10 |
10 |
11 |
|
(18) |
1 |
−4 |
3 |
1 |
|
|
1 |
−4 |
3 |
1 |
|
|
−1 |
−6 |
7 |
10 0 |
0 |
0 |
0 |
|
||||
Последняя строка матрицы справа может быть записана как уравнение
0x1 + 0x2 + 0x3 = 0,
которое имеет место при любых x1, x2 è x3. Наличие или отсутствие этого уравнения не влияет на множество решений системы. Следовательно, послед-
нюю строку матрицы справа в формуле (18) можно вычеркнуть:
1 |
−4 |
3 |
1 . |
|
0 |
− |
10 |
10 |
11 |
|
||||
Полученная матрица является ступенчатой. Этой матрице, эквивалентной матрице Aр, соответствует следующая система, равносильная исходной:
( |
1 |
−10x2 |
+ |
10x3 |
= 11. |
(19) |
x |
|
4x2 |
+ |
3x3 |
= 1, |
|
−
Система (19) имеет ступенчатый вид, и число r уравнений в ней меньше числа n переменных (2 < 3). Подобные системы имеют бесконечное множество n − r параметров. Для нахождения общего решения системы переменные разделяются на r основных (иначе, базисных ) и n −r сво-
бодных (параметров). В качестве основных переменных в можно брать любой
набор из r переменных, определитель матрицы коэффициентов при которых
не равен нулю. Так, за основные переменные всегда можно взять, например, те, что стоят "на ступеньках" преобразованной системы. При этом свободным переменным можно независимо друг от друга присваиваются произвольные значения, а основные переменные с помощью обратного хода метода Гаусса (вверх с последнего уравнения к первому) выражаются через свободные.
В нашем примере система имеет бесконечное множество решений, зависящее от одного (n − r = 3 − 2 = 1) параметра. Переменные разделим на 2 основных
è 1 свободную. За основные переменные можно взять x1 è x2
|
|
0 |
−10 |
|
= 1 · (−10) − 0 = −10 6= 0 . |
|
1 |
4 |
|
||
|
|
− |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
27

Переменная x3 в этом случае будет свободной (параметром):
x3 = C, C произвольное действительное число .
Двигаясь по системе (19) "снизу вверх", последовательно находим переменные
x2 è x1: |
|
|
11 − 10x3 |
|
11 − 10C |
|
|
|
|
|
|
|
x |
2 |
= |
= |
= C |
− |
1, 1; |
|
|
||||
|
|
|
10 |
10 |
|
|
|
|
|
|||
|
|
|
− |
|
|
− |
|
|
|
|
|
|
x1 = 1 + 4x2 − 3x3 = 1 + 4(C − 1, 1) − 3C = C − 3, 4. |
|
|||||||||||
Èòàê, |
|
|
|
|
x2 = C − 1, 1; |
|
|
|
|
|
||
x1 = C − 3, 4; |
x3 = C |
(20) |
||||||||||
(C произвольная постоянная) общее решение исходной системы. Для нахождения какого-нибудь частного решения возьмем произвольное значение C и подставим его в формулы (20). Полагая, например, C = 0, получим:
x1 = −3, 4; x2 = −1, 1; x3 = 0
частное решение исходной системы.
Замечание 78. Частное решение системы линейных уравнений, в котором все свободные переменные равны нулю, называется базисным.
Так, найденное в примере 77 частное решение является также и базисным.
Пример 79. С помощью метода Гаусса найдем общее и некоторое частное решение системы линейных уравнений
(6x1 |
+ 9x2 |
+ 5x3 |
2x4 |
= 5. |
2x1 |
+ 3x2 |
− x3 |
+ 7x4 |
= −2, |
−
Запишем расширенную матрицу системы:
|
6 |
9 |
5 −2 |
5 |
Að = |
2 |
3 |
−1 7 |
−2 . |
|
|
|
|
|
Выполним элементарные преобразования над матрицей. Обнулим второй элемент первого столбца, для чего умножим первую строку на (−3) и прибавим ее к третьей:
6 |
9 |
5 −2 |
5 |
|
0 |
0 |
8 −23 |
11 |
|
2 |
3 |
−1 7 |
−2 |
|
2 |
3 |
−1 7 |
−2 |
|
|
|
|
|
|
|
|
|
|
|
Поменяем местами второй и третий столбец, учитывая при этом, что пере- менные x2 è x3 также поменяются местами:
|
0 |
8 |
0 |
−23 |
11 |
|
2 |
−1 |
3 |
7 |
−2 . |
|
|
|
|
|
|
Матрица приведена к ступенчатому виду. Этой матрице, эквивалентной матрице Að соответствует следующая система, равносильная исходной:
( |
−8x3 |
|
23x4 |
= 11 |
|
2x1 |
x3 |
+ 3x2 + 7x4 |
= −2, |
(21) |
|
|
|
− |
|
|
|
28

(напомним, что менялись местами столбцы матрицы, а с ними и переменные x2 è x3). Система (21) имеет ступенчатый вид, число r = 2 уравнений в ней меньше числа n = 4 переменных. Существует бесконечное множество решений системы, зависящее от двух ( n−r = 4−2 = 2) параметра. Переменные разделим на 2 основных и 2 свободных. За основные переменные можно взять x1 è x3,
стоящие "на ступеньках" |
системы. Переменные x2 è x4 будут свободными |
(параметрами): |
|
x2 = C1, x4 = C2 |
C1, C2 произвольные действительные числа . |
Двигаясь по системе (21) "снизу вверх", последовательно находим переменные x3 è x1:
|
|
|
|
|
|
|
x3 = |
|
11 + 23x4 |
= |
23 |
|
|
C2 |
+ |
11 |
; |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
23 |
|
|
|
|
|
11 |
|
|
|
|
|
|
||||||||||||
x1 = |
−2 + x3 − 3x2 − 7x4 |
= |
|
|
−2 + |
|
|
|
|
C2 + |
|
|
|
− 3C1 − 7C2 = |
||||||||||||||||||||||||||||||
2 |
|
|
|
2 |
|
8 |
|
8 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
33 |
|
|
|
|
5 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
33 |
|
|
|
|
5 |
|
|
||||||||||||
|
|
= |
|
2 |
|
−3C1 − |
8 |
|
C2 − |
|
8 |
|
|
= − |
|
2 |
|
C1 − |
16 |
|
C2 − |
16 |
. |
|||||||||||||||||||||
Èòàê, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
33 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
11 |
|
|
|
|
||||||
x1 = − |
|
C1 − |
|
C2 − |
|
; |
|
|
|
x2 = C1; |
|
|
|
x3 = |
|
|
C2 |
+ |
|
; |
|
|
x4 = C2 (22) |
|||||||||||||||||||||
2 |
16 |
16 |
|
|
|
|
|
|
8 |
8 |
|
|
||||||||||||||||||||||||||||||||
(C1, C2 не зависящие друг от друга произвольные постоянные) общее решение исходной системы. Для нахождения какого-нибудь частного решения
выберем произвольным образом значения C1 è C2 и подставим их в формулы (22). Полагая, например, C1 = C2 = 0, получим:
x1 = − |
5 |
; x2 |
= 0; x3 = |
11 |
; x4 |
= 0 |
|
16 |
|
8 |
|||||
частное (базисное) решение исходной системы.
1.6. Лекция 6.
1.6.1. Векторы на плоскости и в пространстве: геометрическая точка зрения.
Определение 80. Пусть на плоскости или в пространстве заданы точки A
èB. Вектором a=AB называется направленный отрезок (см. рис. 12) ñ íà÷à-
лом в точке A и концом в точке B, который можно перемещать параллельно самому себе.
Ðèñ. 12.
29
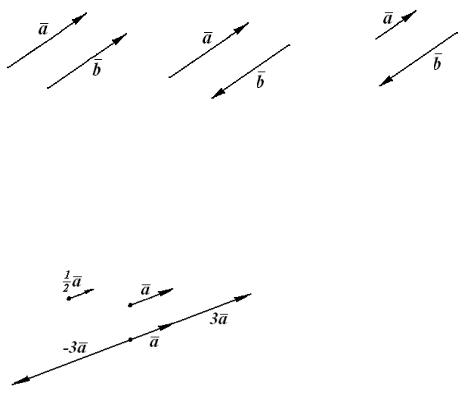
Определение 81. Длиной (модулем) вектора называется длина отрезка,
изображающего вектор. Обозначение: |
|
− |
|
длина вектора |
− |
|
| |
a |
| |
a. |
|||
|
|
|
|
Определение 82.
è единичным, если его длина равна единице.
Определение 83. Два вектора называются равными, если они: 1) лежат на одной прямой или параллельных прямых; 2) имеют равные длины; 3) на-
правлены в одну сторону.
− −
Так, векторы a è b, изображенные на рисунке 13, являются равными.
Определение 84. Два вектора называются противоположными, если они: 1) лежат на одной прямой или параллельных прямых; 2) имеют равные длины;
3) направлены в разные стороны.
− −
Так, векторы a è b, изображенные на рисунке 14, являются противоположными.
Определение 85. Два вектора называются коллинеарными (параллельными),
если они лежат на одной прямой или параллельных прямых. |
|
||
− |
è |
− |
|
Так, векторы a |
|
b, изображенные на рисунке 15, являются коллинеарными. |
|
Ðèñ. 13. |
|
Ðèñ. 14. |
Ðèñ. 15. |
|
|
|
|
|
− |
|
|
|
|
Определение 86. Произведением вектора a на число λ называется вектор |
|||||||||
− такой, что он: 1) лежит с вектором |
− |
|
|
||||||
на одной прямой или параллельных |
|||||||||
λ a |
|
− |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямых; 2) имеет длину, равную |
|λ|| |
a |
| |
; направлен в одну сторону с вектором |
|||||
− |
|
|
|
|
|
|
|
||
a, åñëè λ > 0 и в противоположную, если λ < 0. |
|
|
|
||||||
|
|
|
|
− |
− |
−, |
1 |
−. |
|
На рисунке 16 изображены векторы a, 3 a, −3 a |
3 |
a |
|||||||
Ðèñ. 16.
30
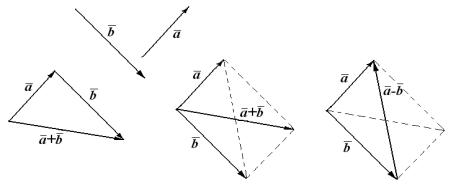
Сложение векторов определяется с помощью правила треугольника èëè ïðà-
вила параллелограмма . |
|
|
|
|
|
|
− |
совпадает с концом вектора − |
|
Определение 87. Пусть конец вектора a |
− |
b, òî- |
||
ãäà суммой этих векторов называется вектор |
− |
|||
a + b, начало которого совпадает |
||||
−, а конец с концом вектора |
− |
|||
с началом вектора a |
|
|
|
b (правило треугольника, см. |
ðèñ. 17, первый из нижних чертежей). |
|
|
||
|
|
|
− |
è − |
Определение 88. Пусть начала векторов a |
b совпадают, тогда суммой |
|||
этих векторов называется вектор |
− |
− |
|
|
a + b, лежащий на диагонали параллело- |
||||
грамма, построенного на векторах |
− è |
− |
|
|
a |
b (правило параллелограмма, см. рис. |
|||
17, второй из нижних чертежей). |
|
|
|
|
Операции сложения векторов и умножения вектора на число называются
|
− |
− |
− |
− |
линейными. Разность векторов a |
− b можно определить как a +(−1) |
b, à |
||
можно воспользоваться следующим определением. |
|
|
||
|
|
− è |
− |
|
Определение 89. Пусть начала векторов a |
b совпадают, тогда разно- |
|||
− |
− |
|
|
− |
ñòüþ a |
− b является вектор, начало которого совпадает с концом вектора b, |
|||
|
− |
|
|
|
а конец с концом вектора a (ñì. ðèñ. 17, третий из нижних чертежей). |
||||
Ðèñ. 17.
1.6.2. Векторы на плоскости и в пространстве: алгебраическая точка зрения.
Во многих приложениях математики, в том числе экономических, векторы удобно рассматривать не как геометрические, а как алгебраические объекты. Это достигается следующим образом. Каждому вектору на плоскости (в пространстве) однозначно соответствует упорядоченная пара (соответственно, тройка) чисел, которые называются координатами или компонентами вектора и определяются как разность соответствующих координат конца и начала век-
тора. Таким образом, если на плоскости заданы точки A(x1, y1) è B(x2, y2), òî
(x2 − x1, y2 − y1) (запись: AB= (x2 − x1, y2 − y1)). Если же заданы точки A(x1, y1, z1) è B(x2, y2, z2) в пространстве, то вектор AB
31

имеет координаты (x2−x1, y2−y1, z2−z1) (запись: AB= (x2−x1, y2−y1, z2−z1)).
Геометрический смысл координат вектора состоит в следующем: первая координата вектора показывает, насколько точка, двигаясь из начала вектора в его
конец, переместилась вдоль оси Ox (с учетом направления); вторая координата характеризует аналогичное перемещение вдоль оси Oy, третья (для векторов
−
в пространстве) вдоль оси Oz. На рис. ?? построен вектор a= (a1, a2) на плоскости и указаны соответствующие перемещения.
Все определения и операции над векторами из пункта 1.6.1 можно переве-
сти на язык координат, являющийся часто более удобным способом описать векторы. Соответствующие свойства опишем с помощью следующих теорем.
−
Теорема 90. Длина (модуль) вектора a= (a1, a2) на плоскости находится так:
q
−
| a | = a21 + a22.
−
Аналогично, длина (модуль) вектора a= (a1, a2, a3) в пространстве находится так:
q
−
| a | = a21 + a22 + a23.
Теорема 91. Вектор на плоскости или в пространстве является нулевым, тогда и только тогда, когда все его координаты равны нулю.
|
|
− |
|
|
|
− |
, a2, a3) â |
Теорема 92. |
Вектор |
a |
= (a1, a2) на плоскости (вектор a= (a1 |
||||
пространстве) является единичным тогда и только тогда, когда |
|
||||||
a2 |
+ a2 = 1 |
|
(соответственно, a2 |
+ a2 |
+ a2 = 1). |
|
|
1 |
2 |
|
|
1 |
2 |
3 |
|
|
|
|
− |
− |
|
|
|
Теорема 93. |
Два вектора a= (a1 |
, a2) è b= (b1, b2) на плоскости являют- |
|||||
ся равными тогда и только тогда, когда одновременно выполнены следующие равенства:
|
a1 = b1, |
a2 = b2. |
|
|
− |
|
− |
Аналогично, два вектора |
a= (a1 |
, a2, a3) è b= (b1, b2, b3) в пространстве явля- |
|
ются равными тогда и только тогда, когда одновременно выполнены следующие равенства:
a1 = b1, |
a2 = b2, a3 = b3. |
− |
− |
Теорема 94. Два вектора a= (a1, a2) è b= (b1, b2) на плоскости являются
противоположными тогда и только тогда, когда одновременно выполнены следующие равенства :
|
a1 = −b1, |
a2 = −b2. |
|
|
− |
|
− |
Аналогично, два вектора |
a= (a1 |
, a2, a3) è b= (b1, b2, b3) в пространстве явля- |
|
ются равными тогда и только тогда, когда одновременно выполнены следующие равенства:
a1 = −b1, a2 = −b2, a3 = −b3.
32
