ПАВ_курс лекций

Величина σкр практически не зависит от природы и свойств наносимых жидкостей и, в основном, определяется свойствами смачиваемого твердого материала. Поэтому можно принять, что величина σкр соответствует его поверхностному натяжению σтв-газ. То, что σкр≈ σтв-газ , можно доказать, используя правило Антонова, согласно которому, межфазное натяжение на границе двух несмешивающихся жидкостей равно разности поверхностных натяжений их взаимно насыщенных растворов.

Применяя это правило для случая взаимодействия жидкости с твердой поверхностью, когда она полностью смачивается, получаем:

Следовательно, при полном смачивании твердого тела σтв-газ = σж-газ и σкр = σтв-газ. Необходимо отметить, что последнее равенство выполняется не всегда, так как для его соблюдения необходимо, чтобы межфазное натяжение σж-тв было равно нулю, или хотя бы величины σтв-газ и σж-газ значительно превышали значение σж-тв. Как правило, эти условия реализуются лишь в случае низкоэнергетических подложек, а для высокоэнергетических поверхностей не выполняется. Поэтому для последних данный метод использовать нецелесообразно. Таким образом, мы рассмотрели основные методы определения межфазных натяжений. Конечно, существует еще много методов определения σ, о которых можно прочитать в специальной литературе. В заключении рассмотрим конкретные примеры решения типовых задач.

Примеры решения типовых задач

Задача 1. Рассчитайте поверхностное натяжение водного раствора ПАВ, если усилие отрыва от его поверхности платиновой пластинки составляет 25,56 мН. Размеры пластинки: 1,2 0,1 1,0 см; плотность платины

– 21,5 г/см3; плотность водного раствора ПАВ − 1,0 г/см3.

21

Решение:

По аналогии с уравнением, приведенным для метода отрыва пластины, для пластинки можно записать:

,

где F – сила отрыва платины; P – вес пластины; П – периметр основания пластины, касающийся поверхности жидкости.

( )

(при расчете веса пластины плотностью жидкости можно пренебречь)

ж⁄

Задача 2. Рассчитайте межфазное натяжение на границе вода-масло, если масса 20 капель четыреххлористого углерода, собранных в контейнере, наполненном водой, оказалась равна 0,84 г. Плотность CCl4 = 1,6 г/см3, плотность H2O = 1,0 г/см3. Эксперименты проводились с использованием метода веса-объема капли, причем внутренний радиус стеклянного капилляра составлял 0,3 см; внешний – 0,4 см. При расчетах нужно учесть неполный отрыв капли, а также то, что органическая жидкость плохо смачивает стекло.

Решение:

Согласно закону Тэйта, вес одной капли четыреххлористого углерода рассчитывается по уравнению: или .

Тогда без учета поправок на неполный отрыв капли:

Объем одной капли CCl4 легко рассчитать, зная общую массу капель и их количество:

( )

И тогда без поправок:

22

( )

(поскольку органическая жидкость не смачивает стекло, то при расчетах берут внутренний радиус капилляра).

Для того, чтобы учесть неполный отрыв капли от капилляра, необходимо вычислить соотношение r/V1/3.

√

Данному значению соответствует величина F = 0,6160 (см. табл. 3 поправочных коэффициентов и используя метод интерполяции).

Тогда с учетом поправки:

Сравните значения рассчитанных межфазных натяжений и убедитесь в необходимости поправки на неполный отрыв капли от капилляра.

Задача 3. Рассчитайте межфазное натяжение на границе жидкостьжидкость, разность плотностей которых составляет ρ = 0,2 г/см3. Расстояние между концом капилляра и границей раздела фаз на приборе Пугачевича (см. рис. 9) составляет h = 1,2 см. Радиус капилляра – 0,2 см. При расчете учтите несферичность капли.

Решение:

В момент достижения максимального избыточного давления Рmax условия механического равновесия на срезе капилляра 3 радиуса r и на границе раздела фаз в манометрической трубке 1 могут быть выражены соответствующими уравнениями:

ж ж

все обозначения соответствуют рис. 9 и условию задачи.

23

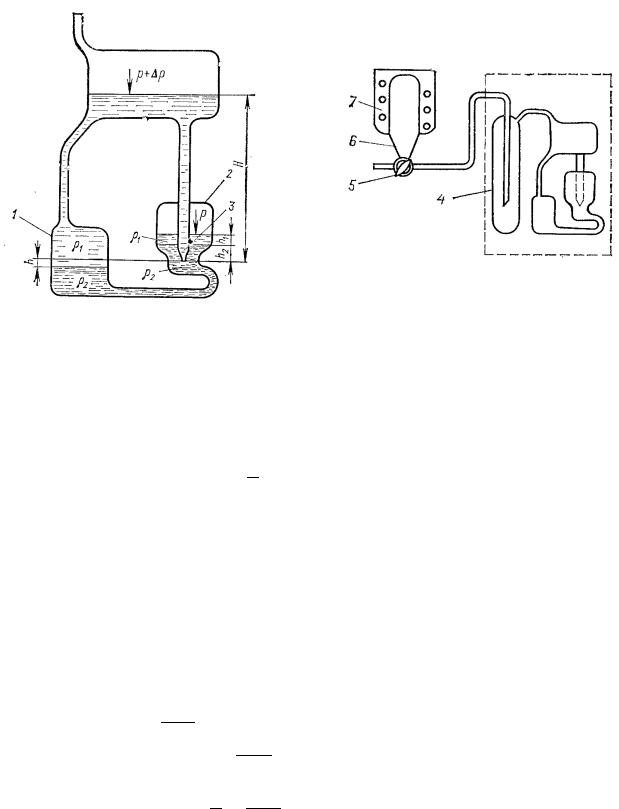
Рис. 9. Схема установки Пугачевича. Слева – схема ячейки для измерения межфазного натяжения; справа – схема прибора УГАЗП-1 КТ:

1 – манометрическая трубка; 2 – приемник; 3 – капилляр; 4 – резервуар; 5 – трехходовой кран; 6 – баллон; 7 – электропечь

Из совместного решения этих уравнений получаем выражение для расчета межфазного натяжения:

ж ж ( )

Преимуществом прибора Пугачевича является то, что в полученное расчетное уравнение не входит краевой угол.

Без учета поправки можно рассчитать σ ж-ж :

ж ж

Для учета несферичности капли рассчитаем первую капиллярную постоянную а1:

( )

√( )

Этому соотношению r/a в табл. 2 поправочных коэффициентов соответствует значение X/r, равное 0,889 (рассчитанное методом интерполяции). Тогда значение Х1, равное 1 капиллярной постоянной:

24

( )

Это значение соответствует новому значению радиуса капилляра с учетом несферичности капли, т.е. при расчетах предполагается, что меняется только значение радиуса капилляра, а величина h остается постоянной. Значение второй капиллярной постоянной с учетом нового значения радиуса будет равно:

сюда Х2 = 0,904 0,18 = 0,162 (см).

Далее аналогично рассчитывают значения следующих капиллярных постоянных до тех пор, пока значения предыдущей и последующей капиллярной постоянной не будут близки. В частности, в данном случае а3 ≈ а4

(0,442≈0,448).

Тогда с учетом последнего значения капиллярной постоянной рассчитывают значение межфазного натяжения:

ж ж

Сравните значения рассчитанных межфазных натяжений и убедитесь в необходимости поправки на несферичность капли.

Рекомендуемая литература:

1.Адамсон А. Физическая химия поверхностей. М.: Мир, 1979.

2.Лабораторные работы и задачи по коллоидной химии / под ред. Ю.Г. Фролова и А.С. Гродского. М.: Химия, 1986.

3.Практикум по технологии косметических средств. Коллоидная химия поверхностно-активных веществ и полимеров / под ред. В. Кима и А.С. Гродского. М.: Изд-во Топ-книга, 2003.

4.Фролов Ю.Г. Курс коллоидной химии: поверхностные явления и дисперсные системы. М.: Химия, 1982. ( 3 изд. − 2004).

25

ЛЕКЦИЯ 3. АДСОРБЦИОННЫЕ РАВНОВЕСИЯ

Как уже отмечалось ранее, ПАВы снижают межфазное натяжение благодаря их высокой адсорбционной способности на различных границах раздела фаз. Остановимся подробнее на рассмотрении явления адсорбции и вначале вспомним основные положения, известные из общего курса коллоидной химии.

Адсорбция представляет собой самопроизвольное перераспределение компонентов между объемной фазой и поверхностным слоем. Компонент системы, который переходит из объема на поверхность, называется адсорбатом; а фаза, формирующая поверхность, − адсорбентом.

Для количественного описания процесса адсорбции применяют две величины. Первая из них называется абсолютной адсорбцией А и представляет собой число молей (граммов) адсорбата, приходящихся на единицу площади поверхности или единицу массы адсорбента. При рассмотрении абсолютной адсорбции используют метод конечной толщины, предложенный Гуггенгеймом. Вторая характеристика адсорбции Г определяется избытком числа молей адсорбата в поверхностном слое определенной толщины по сравнению с его количеством в таком же объеме объемной фазы, также отнесенным к единице поверхности или массы адсорбента. При рассмотрении этой величины используют метод Гиббса (метод избыточных величин), поэтому величину Г часто называют избыточной (гибб-

совской) адсорбцией.

Рассмотрим кратко методы Гуггенгейма и Гиббса, начиная с первого (метод слоя конечной толщины или метод Гуггенгейма).

Рассмотрим простую систему, состоящую из бинарного истинного раствора и твердого адсорбента и находящуюся при постоянной температуре. Для ясности представим себе, что этот бинарный раствор состоит из синего красителя (метиленового голубого) – адсорбата, и воды в качестве растворителя. Понятно, что если краситель растворяется в воде с образованием истинного раствора, то раствор окрашивается в голубой цвет. Введем в этот раствор твердый адсорбент, например, активированный уголь, и оставим полученную систему на некоторое время. После достижения равновесия увидим, что интенсивность окраски раствора уменьшилась – из

26

интенсивно синего раствор стал бледно-голубым. Это значит, что часть красителя перешла из раствора (объемной фазы) на поверхность активированного угля, т.е. произошла адсорбция красителя на поверхности твердого адсорбента. Получим уравнение для расчета величины адсорбции.

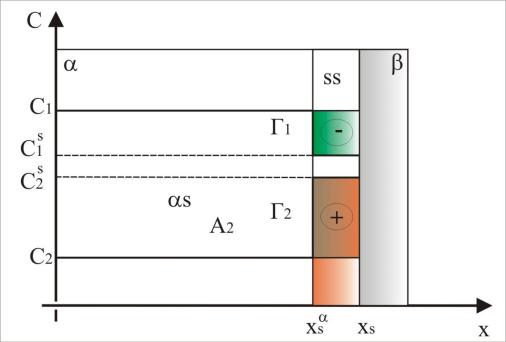
Для этого воспользуемся схемой, которая иллюстрирует описанный выше опыт (рис. 10).

Рис. 10. К расчету абсолютной и гиббсовской адсорбции

Бинарный раствор красителя в воде обозначим фазой , твердый адсорбент – активированный уголь – фазой . По оси ординат будем откладывать концентрацию с моль/л, по оси абсцисс – некоторую координату x, характеризующую изменение свойств системы в зависимости от расстояния от поверхности раздела. Допустим, что на поверхности раздела между раствором и твердым адсорбентом формируется адсорбционный слой, заключенный между xs и x s, где xs – координата, где поверхность твердого адсорбента граничит с поверхностным слоем; x s – координата, где поверхностный слой граничит с объемной фазой . Тогда толщину поверхностного слоя можно обозначить h и выразить как (xs − x s). На рисунке сплошной линией показан профиль концентраций компонента с2 (здесь и далее

27

нижний индекс «2» будет характеризовать все параметры, относящиеся к растворенному веществу, а индекс «1» − к растворителю).

Для простоты допустим, что в процессе адсорбции концентрация адсорбата резко ступенчато возрастает в поверхностном слое, достигнув величины с2s . Тогда общее число молей адсорбата (n2), находящееся в системе, можно вычислить следующим образом:

(18)

где n s2 – число молей адсорбата в объемной фазе (до поверхностного слоя); nss2 – число молей адсорбата в поверхностном слое; V s – объем фазыдо поверхностного слоя; Vs – объем поверхностного слоя. Величина адсорбции представляет собой число молей адсорбата в поверхностном слое, отнесенное к единице площади поверхностного слоя, т.е.:

(19)

Из-за невозможности экспериментального определения объема и толщины поверхностного слоя, метод Гуггенгейма используется только при проведении термодинамических расчетов. Гиббсом был предложен другой метод определения величины адсорбции, который представлен ниже.

При рассмотрении метода Гиббса будем использовать ту же схему, что и для метода Гуггейгейма − тот же бинарный раствор в равновесии с твердым адсорбентом. Гиббс предложил считать, что поверхностный слой не имеет собственного объема и толщины, число молей адсорбата в таком случае можно выразить так:

( ) (20)

Величина ns2/s представляет собой избыточную (гиббсовскую адсорбцию), обозначаемую большой греческой буквой гамма − Г. По своему физическому смыслу гиббсовская адсорбция представляет собой избыток числа молей компонента в поверхностном слое определенного объема по сравнению с числом молей компонента в объемной фазе такого же объема. В отличие от величины абсолютной адсорбции, этот избыток можно определить экспериментально, зная исходную концентрацию адсорбата до адсорбции и равновесную концентрацию адсорбата после адсорбции. Зави-

28

симость величины адсорбции от равновесной концентрации адсорбата называется изотермой адсорбции.

Сопоставляя эти два метода, можно получить взаимосвязь между абсолютной и гиббсовской адсорбции, а именно:

(21)

Из этого простого выражения вытекает несколько важных выводов. Во-первых, гиббсовская адсорбция, в отличие от абсолютной, может быть отрицательной. Во-вторых, если концентрацией адсорбата в объеме по сравнению с его концентрацией на поверхности можно пренебречь, то величины абсолютной адсорбции и гиббсовской практически совпадают. Те случаи, когда Г<0, здесь рассматриваться не будут; обратим внимание на то, когда А ≈ Г. Это возможно в двух случаях – 1) при адсорбции газов и паров на твердых адсорбентах; 2) при адсорбции поверхностно-активных веществ (ПАВ) из водных растворов.

В заключении вспомним уравнение, связывающее гиббсовскую адсорбцию с величиной межфазного натяжения, называемое фундаментальным уравнением Гиббса:

где i – химический потенциал компонента i.

В частности, для бинарного раствора это уравнение переходит в широко используемое уравнение Гиббса для неэлектролитов:

где R – универсальная газовая постоянная; Т – температура.

На этом, в основном, заканчивается материал, известный из общего курса коллоидной химии. Продвинемся немного далее и представим себе, что концентрацию компонентов можно выразить не в моль/л, как ранее, а в мольных долях – х. Тогда, введя следующие обозначения, получим:

n0 – общее число молей в системе; ns – число молей в поверхностном слое; x02 − мольная доля второго компонента до адсорбции; x2 – равновесная концентрация второго компонента после адсорбции; х2s − концентрация

29

второго компонента в поверхностном слое. Для первого компонента спра-

ведливы те же самые обозначения.

Общее число молей в поверхностном слое можно представить как:

(24)

тогда

Или:

(26)

где

(27)

Г2х и Г1х – величины гиббсовской адсорбции для второго и первого компонентов, в случае, когда их концентрации выражены в мольных долях.

Вернемся к фундаментальному адсорбционному уравнению Гиббса для бинарного раствора:

(28)

и рассмотрим два случая:

а) случай предельно разбавленного раствора, когда изменением химического потенциала первого компонента (растворителя) можно пренебречь. Тогда:

(29)

(30)

(31)

(32)

б) некоторый искусственный случай, когда разделяющая поверхность (см. лекцию 1) выбирается так, чтобы адсорбция первого компонента Г1 была равно 0, т.е. Г1 = 0. Для такого случая справедливы следующие обозначения и уравнение:

30