
ПАВ_курс лекций
.pdf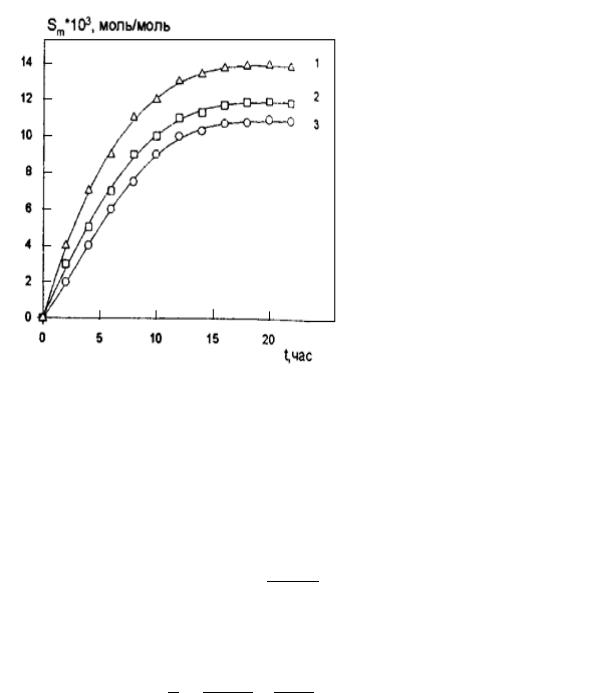
Пример кинетических кривых солюбилизации приведен на рис. 55.
Рис. 55. Кинетические кривые солюбилизации красителя оранжевого – ОТ. ПАВ:
1− ОП-21; 2 – ОП-16,4; ОП – 15,5
Обычно для установления равновесия требуется 20−30 часов. Однако иногда бывает достаточно определить зависимость солюбилизации за некоторый начальный промежуток времени, а затем графически определить предел солюбилизации.
Зависимости, представленные на последнем рисунке, могут быть описаны уравнением:
(129)
где k – константа скорости солюбилизации; t – время. Эти константы могут быть определены по линейной форме данного уравнения (рис. 56):
(130)
Зависимость предела молярной солюбилизации от степени оксиэтилирования неионных ПАВ имеет вид, аналогичный зависимости ККМ:
(131)
где а и b – константы, зависящие от длины углеводородного радикала.
91
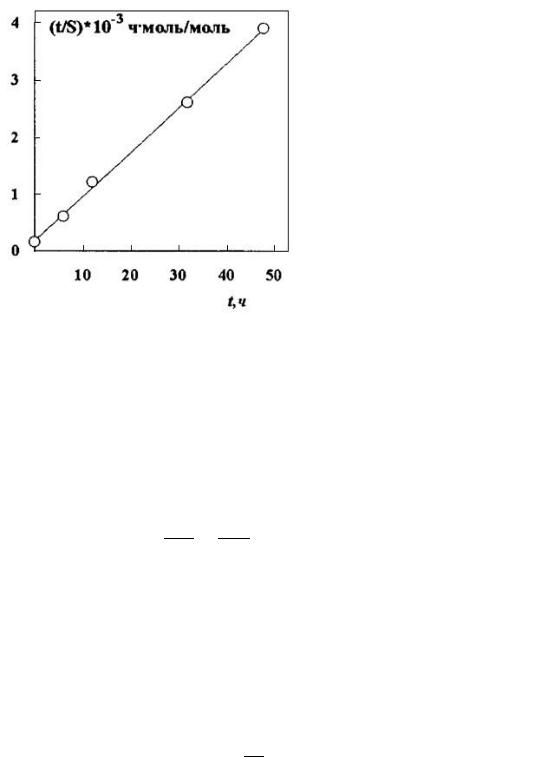
Рис. 56. Кинетическая зависимость в линейных координатах солюбилизации оранжевого – ОТ растворами ОП-16,4
Изменение солюбилизации при повышении температуры описывается уравнением:
( |
|
) |
(132) |
|
|
||
|
|
где ΔGs – изменение свободной энергии при солюбилизации.
И далее для расчета энтальпии солюбилизации используется известное уравнение:
( |
|
|
|
) |
(133) |
|
|
|
|
||
|
|
|
В данном разделе были рассмотрены классические представления о солюбилизации. Далее очень кратко коснемся современных взглядов на солюбилизацию, предложенных А.И. Русановым.
Введем понятие солюбилизационной емкости S, предварительно обозначив индексом «1» − ПАВ; «2» − солюбилизат (то малорастворимое вещество, которое солюбилизируется).
(134)
Учитывая ранее введенные обозначения, n1 – соответствует ̅, а n2 соответствует ̅.
Рассмотрим физико-химическую суть явления солюбилизации. Всякое перемещение вещества, как и обычное растворение, происходит под действием разности химических потенциалов, которые являются функциями
92

локальных величин температуры, давления и состава. В тех местах, где данного вещества совсем нет, при нулевой концентрации химический потенциал и, следовательно, диффузионный перенос туда данного вещества обязательно будет происходить, пока химические потенциалы не выровняются. Введем некоторые обозначения, соответствующие рис. 56:
Рис. 57. Схема солюбилизации:
α – внутренная фаза мицеллы; β – внешняя фаза, окружающий мицеллу раствор;
γ – фаза чистого солюбилизируемого вещества
При равенстве химических потенциалов μα в мицелле и μγ – в фазе γ
можем записать: |
|
|
|
|
( ) |
( |
|
) |
(135) |
|
|
|||
( ) |
|
где с2(r) − локальная концентрация солюбилизата в точке r внутри мицеллы; W(r) − работа переноса одной молекулы солюбилизата из собственной фазы в эту точку.
Поскольку концентрация в фазе чистого солюбилизата c2γ > c2(r), то представленная работа является величиной положительной, т.е. при переносе одной молекулы солюбилизата в мицеллу работа затрачивается, а не выигрывается. Возникает вопрос о том, на что же затрачивается эта работа?
Можно предположить, что работа затрачивается на преодоление Лапласовского давления:
(136)
93

Действительно, при переносе солюбилизата из фазы γ внутрь мицеллы, пересекается одна плоская поверхность (βγ) и одна искривленная (αβ). Следовательно, в соответствии с уравнением Лапласа, осуществляется переход от давления к давлению  .
.
Если рассматривать перенос молекулы углеводорода в ядро прямой мицеллы, сформированной также углеводородными хвостами, то, пренебрегая межмолекулярными взаимодействиями, можно принять, что работа переноса сводится к преодолению лапласовской разности давлений:
( ) |
( |
) |
(137) |
где ν2 − парциальный молекулярный объем углеводорода. С учетом вышесказанного, можем записать:
( |
) |
( |
|
) |
(138) |
|
|
||||
|
|
Необходимо еще раз обратить внимание на то, что все, представленное выше касалось именно прямых мицелл (см. рис. 57). К случаю солюбилизации воды в обратных мицеллах эти приближения не годятся из-за того, что перенос воды внутрь обратной мицеллы сопровождается существенным изменением межмолекулярных взаимодействий.
Последнюю представленную здесь формулу интересно использовать для оценки поверхностного натяжения прямых мицелл. Если оценить как реальную среднюю концентрацию солюбилизата в углеводородном ядре, то в предположении аддитивности объема, можно записать:
(139)
( ⁄ )
(140)
Тогда лапласовское давление может быть рассчитано как:
( |
|
) |
(141) |
|
|
||
|
|
94

Из этого уравнения видно, что солюбилизационная емкость определяется капиллярной (лапласовской) разностью давлений (в общем случае – работой переноса).
Данные теоретические рассуждения были использованы для расчета солюбилизации конкретными ПАВ. В частности, при солюблизации олеатом натрия октана было получено следующее. Солюбилизационная ем-
кость составила s = 0,5. Объем углеводородного радикала |
олеат-иона |
. Парциальный мольный объем октана |
. |
При Т = 293 К лапласовское давление приблизительно составило
. Для того чтобы, используя эти экспериментальные данные, оценить поверхностное натяжение мицелл, используем уравнение Лапласа, принимая, что радиус кривизны в данном случае соответствует радиусу ядра мицеллы олеата натрия = 2,5 нм.
(142)
Полученное значение поверхностного натяжения мицелл составило 28,5 мН/м. С общефизической точки зрения полученная величина кажется вполне разумной.
Для других ПАВ и солюбилизатов можно получить несколько иные значения, однако, можно говорить о том, что величина поверхностного натяжения мицелл колеблется в пределах от 25 до 38 мН/м. Здесь же необходимо отметить, что математически показано, что непосредственно в ядре мицеллы находится не более 10% солюбилизата, а чаще – значительно меньше; т.е. из ядра мицеллы углеводород самопроизвольно распределяется по периферии.
Заканчивая рассмотрение солюбилизации, необходимо отметить, что можно продолжить начатые рассуждения и для несферических мицелл, однако, в данном курсе это показано не будет.
В заключение можно отметить практические области применения солюбилизации. Солюбилизация – один из определяющих факторов моющего действия растворов ПАВ. Поэтому она давно используется в человеческой практике. Особенно широкое распространение солюбилизация получила в современных химических технологиях, где она заменяет использо-
95
вание органических растворителей, играет важную роль в механизме мицеллярного катализа, эмульсионной полимеризации, разделения веществ в аналитических целях и извлечения нефти из обедненных пластов. Солюбилизация в обратных мицеллах используется в процессах сухой чистки. Велико значение солюбилизации и для биологических систем. Если рассматривать не практическую, а научную сторону вопроса, то исследуя солюбилизацию можно получить информацию о значениях ККМ и строении мицелл.
6. Везикулы. Строение и основные свойства
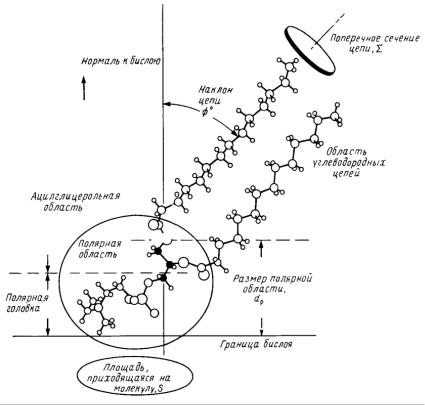
При определенном строении молекулы ПАВ, с достижением критической концентрации, кроме мицелл, возможно образование везикул. Обычно легко образовывают везикулы те ПАВ, в молекуле которых есть два углеводородных хвоста. Поэтому природными везикулами являются везикулы фосфолипидов (липосомы). Как известно, молекула большинства фосфолипидов содержит два и более углеводородных радикала и может быть представлена так, как на рис. 58.
Рис. 58. Строение молекулы фосфолипида (фосфатидилхолина)
96
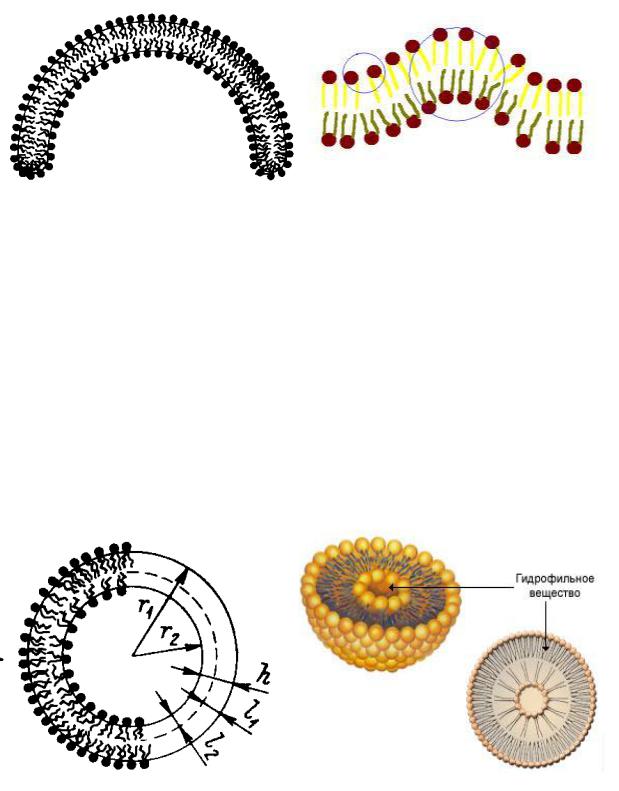
Если мицеллу можно представить себе как замкнутый на себя монослой, то везикулу – как замкнутый на себя бислой, как показано на схеме
(рис. 59).
Рис. 59. Замкнутый на себя бислой
При этом нельзя забывать о том, что и мицелла, и везикула являются объемными, не плоскими образованиями. Т.е., грубо говоря, везикула – это «мячик в мячике», а не плоский «бублик». Как и мицеллы, везикулы бывают прямыми и обратными в зависимости от строения внешнего и внутреннего слоя. Как и в случае мицелл, в воде образуются прямые везикулы, в органической среде – обратные. При рассмотрении везикул необходимо также помнить о том, что и внешний, и внутренний слой образован одними и теми же молекулами ПАВ, однако истинная длина радикала (хвоста) и величина посадочной площадки молекулы ПАВ во внешнем и внутреннем слое различаются.
Рассмотрим строение прямой везикулы (рис. 60):
Рис. 60. Схема прямой везикулы
97

Для внешнего слоя параметр упаковки Ns близок к единице и посадочную площадку a1 ПАВ можно рассчитать по нижеприведенному уравнению, используя обозначения рисунка.
(143)
(144)
[ ]
Для внутреннего слоя посадочная площадка меньше и рассчитывается по уравнению:
(145)
[ ]
где V – средний объем молекулы ПАВ.
Многочисленными исследованиями показано, что во внешнем слое углеводородный радикал может быть максимально вытянут, тогда как во внутреннем слое − нет. Радикалы (хвосты) внешнего и внутреннего слоев могут переплетаться и проникать друг в друга, что облегчает упаковку везикул. В любом случае, толщина h < 2lc, где lc − длина вытянутого радикала.
Обычно, чаще всего ⁄ , т.е. минимальная площадь на 1 молекулу ПАВ во внутреннем монослое меньше, чем во внешнем. При этом часто внутренняя поверхность везикулы целиком заполнена полярными группами, а внешняя − лишь частично. Если размер полярной группы так
велик, что не выполняется соотношение ⁄ , то формирование вези-
кулы становится невозможным.
В частности, для малых везикул получены следующие экспериментальные данные, представленные на рис. 61.
Необходимо отметить также, что везикула является динамической «живой» системой, в ней отсутствует жестких скелет, и молекулы ПАВ постоянно перескакивают с места на место. Равновесие между двумя монослоями будет достигнуто, когда молекулы ПАВ в этих слоях будут обладать одними и теми же значениями химических потенциалов. Теоретиче-
98
ски это возможно, когда ⁄ , т.е. а1=а2. Тогда степени агрегации n1 и n2 в наружном и внутреннем монослоях будут пропорциональны их поверхностям:
(146)
( )
Рис. 61. Поперечное сечение бислоя в малых моноламеллярных везикулах с указанием ряда характерных размеров
Однако, даже при равенстве посадочных площадок в монослоях, на внутренней поверхности везикулы наблюдается более сложная конформационная картина углеводородных цепей.
Везикулы отличаются достаточно большой солюбилизационной емкостью. При описании процесса солюбилизации может быть использован подход А.И. Русанова, рассмотренный для мицелл.
7. Мицеллярная масса. Методы ее определения
Для определения мицеллярной массы существует несколько методов определения, наиболее распространенными среди которых являются следующие:
7.1.Метод светорассеяния
Врастворах ПАВ светорассеивающие частицы представляют собой мицеллы, формирующиеся после достижения ККМ. Наиболее распростра-
99
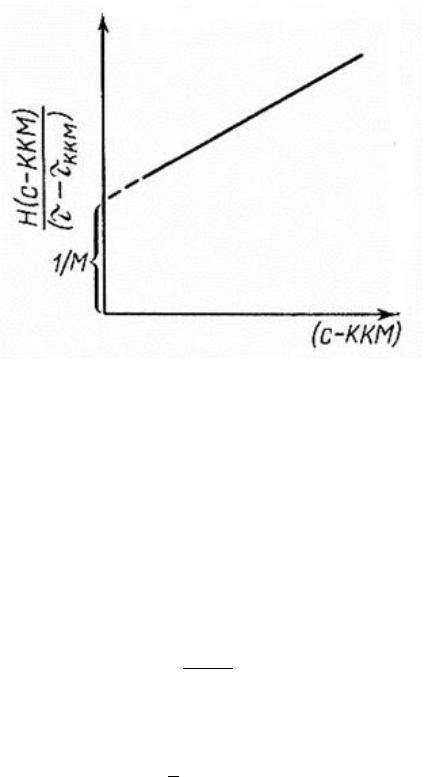
ненным методом, базирующимся на рассеянии света мицеллами ПАВ, является метод Дебая. Метод заключается в измерении мутности растворов ПАВ при различных концентрациях и построении зависимости в следующих координатах, представленных на рис. 62.
Рис. 62. Определение молекулярной массы методом Дебая
На рисунке отсечка на оси ординат − величина, обратная мицеллярной массе; Н – константа Дебая; τ − мутность раствора ПАВ при определенной концентрации, τ ККМ – мутность раствора при достижении ККМ.
7.2. Комбинированный метод измерения диффузии и вязкости
Вторым по широте применения (после метода светорассеяния) является комбинированный метод измерения диффузии и вязкости. Для сферических мицелл, перемещающихся в жидкой среде, коэффициент трения связан с коэффициентом диффузии уравнением Эйнштейна:
(147)
Умножив объем одной мицеллы на плотность ПАВ (ρ2) и число Авогадро, получаем «мицеллярную» молекулярную массу:
(148)
100
