
ПАВ_курс лекций
.pdf
(33)
где а2 – активность второго компонента.
Данное уравнение справедливо для любых концентраций, а не только для предельно разбавленных растворов.
Итак, для бинарных растворов можно записать серию уравнений:
(34)
(концентрация выражена в моль/л);
(35)
(концентрация выражена в мольных долях);
(36)
(когда Г1 = 0).
Далее приводится несколько уравнений, позволяющих предсказать вид изотермы гиббсовской адсорбции. Вне зависимости от способа выражения концентраций избыточную гиббсовскую адсорбцию можно обозначить как Г1 и Г2 для первого и второго компонентов, соответственно. Тогда опять же для бинарного раствора можно записать:
(37)
Кроме фундаментального адсорбционного уравнения Гиббса применим к бинарному раствору уравнение Гиббса−Дюгема:
∑ |
(38) |
|
Объединив два последних уравнения, получаем:
(39)
(40)
( |
|
) |
(41) |
|
|
И, наконец:
31
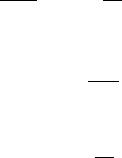
(42)
Учитывая то, что
(43)
можем записать еще одно уравнение для ее расчета:
(44)
Таким образом, величина Г21 определяется однозначно и не зависит от способа выражения концентрации. Мы сами выбираем такое положение разделяющей поверхности, когда Г1 = 0. Остальные же величины гиббсовской адсорбции не равны между собой, т.е. Г2v Г2х (аналогично и первого компонента).
Вернемся опять к мольным долям:
( |
|
) |
(45) |
|
|
и введем такое ограничение, что ns = n1s+n2s = const,
т.е. число молей в поверхностном слое постоянно (грубо говоря, это означает то, что если в этот поверхностный слой что-то приходит, то что-то должно из него уходить). Тогда:
(46)
Запишем без вывода еще несколько уравнений, связывающих между
собой Г2х , Г1х и Г21, не забывая о том, что х1 + х2 = 1. |
|
|||||||||
|
|
( |
|
|
|
|
|
|
) |
(47) |
|
|
|
|
|
|
|
|
(48) |
||
( |
) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
( |
) |
|
|
|
|
|
(49) |
|||
|
|
|
|
|
|
|
|
|
|
(50) |
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
|
||
|
|
32 |
|
|
|
|
|
|
|
|
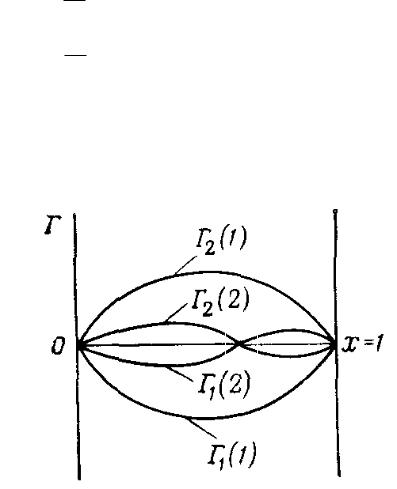
Анализируя совокупность представленных уравнений можно изобразить типичные изотермы гиббсовской адсорбции (рис. 11), рассчитанные по методу избытков Гиббса.
Рассмотрим граничные области представленных изотерм:
1) При х2 = 0, Г2х = 0, т.е. изотермы всегда выходят из начала коорди-
нат.
2) При х2 = 1, Г2х = 0.
3) 0< х2<1 при d <0 Г2х>0 da2
при d >0 Г2х<0 da2
4)Г2х = −Г1х.
5)Точка А, где изотерма пересекает ось абсцисс, называется адсорб-
ционной азеотропией, т.е. при таких концентрациях разделение компонентов невозможно.
А
Рис. 11. Примеры изотерм гиббсовской адсорбции
Запишем еще несколько уравнений, связывающих величины Г и А (гиббсовской и абсолютной адсорбции) и часто использующихся при решении задач:
|
|
и |
|
|
(51) |
|
|
|
(52) |
||||
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
33 |
|
|
|

|
|
|
|
|
(53) |
( |
|
|
|
) |
(54) |
|
|
|
|
||
|
|
|
Наконец, следует упомянуть еще одно выражение:
(55)
где Р – некоторый параметр, являющийся функцией молярных объемов V компонентов. В таком случае последнее выражение можно конкретизировать и записать как:
(56)
(57)
|
( |
|
|
|
) |
(58) |
||||
|
|
|
|
(59) |
||||||
|
|
|
||||||||
( |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
Для того чтобы приведенный в этой лекции материал был усвоен хорошо, рекомендуется самостоятельно выполнить задания, выданные преподавателем.
Рекомендуемая литература:
1.Фролов Ю.Г. Курс коллоидной химии: поверхностные явления и дисперсные системы. М.: Химия, 1982. ( 3 изд. − 2004).
2.Грег С., Синг К. Адсорбция, удельная поверхность, пористость.
М.: Мир, 1984.
3.Белик В.В., Киенская К.И. Физическая и коллоидная химия. М.: Академия, 2005.
4.Джейкок М., Парфит Дж. Химия поверхностей раздела фаз. М.:
Мир, 1984.
34
ЛЕКЦИИ 4−5. ПОВЕРХНОСТНЫЕ ПЛЕНКИ. ПЛЕНКИ ПАВ. РАСТЕКАНИЕ ОДНОЙ ЖИДКОСТИ ПО ПОВЕРХНОСТИ ДРУГОЙ
Исследования пленок малорастворимых веществ на жидких поверхностях интересовали ученых с давних времен. Еще Плиний старший и Плутарх знали об успокаивающем действии масла на бурное море. В 1774 году Б. Франклин дал некоторую количественную характеристику этому явлению: он установил, что одной чайной ложки масла достаточно, чтобы успокоить пруд площадью ~ 0,2 га. Позднее, в 1890 году, Рэлей установил, что хаотическое движение кусочков камфоры по воде прекращается, если на поверхность воды нанести олеиновую кислоту в количестве, необходимом для образования пленки толщиной всего лишь около 16 Å. Это позволило оценить максимальный размер молекулы олеиновой кислоты и ее молекулярный вес и, таким образом, установить значение числа Авогадро.
Приблизительно в то же время Поккельс обнаружила возможность регулирования площади пленки с помощью подвижного барьера. Она, в частности, показала, что поверхностное натяжение пленки изменяется лишь до тех пор, пока удельная поверхность пленки не уменьшится до ~ 20 Å2 на молекулу (точка Поккельс). Позже Рэлей пришел к выводу о том, что
вточке Поккельс молекулы пленки касаются друг друга. Дальнейшие опыты Лэнгмюра показали, что для пальмитиновой, стеариновой и церотиновой кислот предельная площадь в точке Поккельс одинакова и составляет ~ 21 Å2 на молекулу. Тот факт, что изменение длины углеводородного радикала от 16 до 26 атомов углерода не влияет на предельную площадь, означает то, что в точке Поккельс молекулы ориентированы вертикально. Объем молекулы пальмитиновой кислоты, рассчитанный из молекулярного веса и плотности, составляет 495 Å3; на поверхности жидкости 1 молекула занимает только 21 Å2, следовательно, ширина молекулы равна ~ 4,5 Å , а длина – 23 Å. Таким образом, исследуя мономолекулярные пленки, можно получать информацию о размерах молекул. Этот вывод был сделан
вначале XIX века, задолго до изобретения микроскопа.
35
Прежде чем подробно рассматривать пленки ПАВ, остановимся на вопросах растекания одной жидкости по другой и образовании малорастворимых жидких пленок, не обязательно поверхностно-активных.
1. Критерии растекания жидкостей
Количественной характеристикой растекания одной жидкости по поверхности другой, как и в случае растекания жидкости по поверхности твердого тела является коэффициент растекания. В данном случае коэффициент растекания жидкости В по поверхности жидкости А будет обозначаться буквой S.
(60)
где σА, σВ – поверхностные натяжения жидкости А и В; соответственно, σАВ
– межфазное натяжение жидкостей.
Коэффициент растекания по физическому смыслу представляет собой разницу между работами адгезии жидкостей и работы когезии жидкости В:
(61)
Растекание будет наблюдаться в том случае, когда WAB > WBB, т.е. S>0. Как правило, жидкость с низким поверхностным натяжением хорошо растекается по жидкости с высоким поверхностным натяжением (эффект
Марангони), о чем свидетельствует табл. 4.
Ранее нами были рассмотрены различные экспериментальные методы определения поверхностных и межфазных натяжений жидкостей, в данном разделе остановимся еще на двух расчетных методах, предложенных Джирифалко и Гудом, а также Фоуксом.
|
|
|
Таблица 4 |
Коэффициенты растекания жидкостей на воде при 20 ºС |
|||
|
|
|
|
Жидкость В |
SB/A, эрг/см2 |
Жидкость В |
SB/A, эрг/см2 |
|
|
|
|
Изоамиловый спирт |
44,0 |
Нитробензол |
3,8 |
|
|
|
|
Н-Октиловый спирт |
35,7 |
Гексан |
3,4 |
|
|
|
|
Гептальдегид |
32,2 |
Гептан (30 ºС) |
0,2 |
|
|
|
|
Олеиновая кислота |
24,6 |
Дибромэтан |
−3,2 |
|
|
|
|
|
36 |
|
|

Окончание табл. 4
Жидкость В |
SB/A, эрг/см2 |
Жидкость В |
SB/A, эрг/см2 |
||
Этиловый эфир |
20,9 |
о-Монобромтолуол |
−3,3 |
||
пеларгоновой кислоты |
|
|
|
|
|
|
|
|
|
|
|
n-Цимол |
10,1 |
Сероуглерод |
−8,2 |
||
|
|
|
|
|
|
Бензол |
8,8 |
Моноиодбензол |
−8,7 |
||
|
|
|
|
|
|
Толуол |
6,8 |
Бромоформ |
−9,6 |
||
|
|
|
|
|
|
Изопентан |
9,4 |
Иодистый метил |
−26,5 |
||
|
|
|
|
|
|
В частности, для расчета межфазного натяжения Джирифалко и Гуд |
|||||
предлагают следующее уравнение: |
|
|
|
|
|
|
( |
) |
|
|
(62) |
|
|
|
|||
|
|
|
|
||
где Ф является функцией мольных объемов каждой жидкости.
( |
) |
(63) |
Фоукс рассматривает конкретный случай − смачивание воды углеводородами, и для расчета межфазного натяжения вода-углеводород σWH предлагает уравнение:
( |
) |
|
(64) |
|
|||
|
|
где σWH – межфазное натяжение между водой и углеводородом; σW и σH – поверхностное натяжение воды и углеводорода, соответственно; σdW – вклад дисперсионных сил в поверхностное натяжение воды (при 20 ºС σdW
= 21,8 мДж/м2).
При более глубоком исследовании процессов растекания возникает одно осложнение – жидкости, находящиеся в контакте друг с другом, взаимно насыщаются, что приводит к изменению их поверхностных натяжений. Так, σА изменяется до σА(В), а σВ – до σВ(А). Конечный коэффициент растекания после взаимного насыщения фаз также изменится, вплоть до отрицательных значений. В частности, если на поверхность воды нанести бензол, поверхностное натяжение которого существенно ниже, чем у воды, то вначале он быстро растечется, а затем стянется в линзу. Сравнить коэффициенты растекания до и после взаимного насыщения жидкостей можно, используя данные табл. 5.
37
Таблица 5
Начальные и конечные коэффициенты растекания на воде (эрг/см2)
Жидкость |
σB |
σB(A) |
σA(B) |
σAB |
SB(A) |
SB(A)/SA(B) |
SA(B) |
SA(B)/SB(A) |
Изоамиловый |
23,7 |
23,6 |
25,9 |
5 |
44 |
−2,7 |
−54 |
−1,3 |
спирт |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Бензол |
28,9 |
28,8 |
62,2 |
35 |
8,9 |
−1,6 |
−78,9 |
−68,4 |
|
|
|
|
|
|
|
|
|
Сероуглерод |
32,4 |
31,8 |
|
48,4 |
−7 |
−9,9 |
−89 |
|
|
|
|
|
|
|
|
|
|
н-Гептиловый |
27,5 |
|
|
7,7 |
40 |
−5,9 |
−56 |
|
спирт |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CH2I2 |
50,7 |
|
|
41,5 |
−27 |
−24 |
−73 |
|
|
|
|
|
|
|
|
|
|
Изменение коэффициента растекания при взаимном насыщении жидкостей послужило основанием сформулировать приближенное правило (правило Антонова) согласно которому межфазное натяжение двух взаимно насыщенных жидкостей равно разности поверхностных натяжений их взаимно насыщенных растворов на границе с воздухом:
а |
| ( ) |
( )| |
(65) |
|
Используя правило Антонова, можно, не проводя эксперимента, определять межфазное натяжение на границе двух несмешивающихся жидкостей, зная их поверхностные натяжения и учитывая при этом взаимное насыщение жидкостей друг другом.
Как известно, жидкости с меньшим поверхностным натяжением хорошо растекаются по жидкости с большим поверхностным натяжением. Так, в частности, растворы ПАВ хорошо растекаются по воде, образуя при этом пленку ПАВ на ее поверхности. Прежде чем переходить к описанию поверхностных пленок, образованных ПАВ, рассмотрим типичные изотермы поверхностного натяжения растворов ПАВ.
2.Виды изотерм поверхностного (межфазного) натяжения
2.1.Изотермы поверхностного натяжения
Адсорбция ПАВ на межфазной границе, согласно фундаментальному уравнению Гиббса, сопровождается снижением межфазного (поверхност-
38
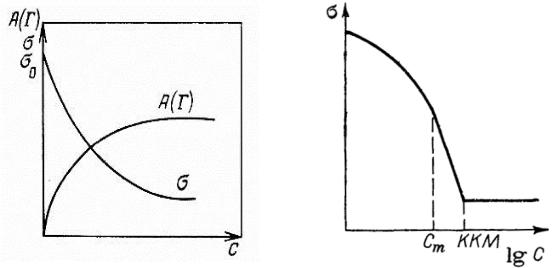
ного) натяжения. В области средних концентраций, где адсорбция ПАВ описывается уравнением Ленгмюра, изотерма поверхностного натяжения описывается уравнением Шишковского (известным из общего курса коллоидной химии):
( |
) |
(66) |
Типичный вид такой изотермы представлен на рис. 12. На рис. 13 показана та же изотерма, построенная в логарифмических координатах. Четкий излом на данной изотерме соответствует критической концентрации мицелообразования (ККМ).
Рис. 12. Типичные изотермы |
Рис. 13. Изотерма поверхностного |
поверхностного натяжения и |
натяжения в логарифмических |
гиббсовской адсорбции |
координатах |
Падение поверхностного натяжения до ККМ обусловлено адсорбцией ПАВ на межфазной границе. Начальный параллельный оси абсцисс участок (рис. 14) имеет место на всех изотермах, если их строить, начиная от достаточно низких концентраций (при очень низких концентрациях ПАВ адсорбция мала и не определяется экспериментально).
Если в системе присутствует несколько ПАВ, резко различающихся по поверхностной активности, то изотерма поверхностного натяжения в ряде случаев имеет ступенчатый вид (рис. 15), однако часто эти ступеньки сливаются в сплошную линию, так что их отсутствие не говорит о чистоте веществ, но их наличие указывает на присутствие в растворе нескольких ПАВ.
39
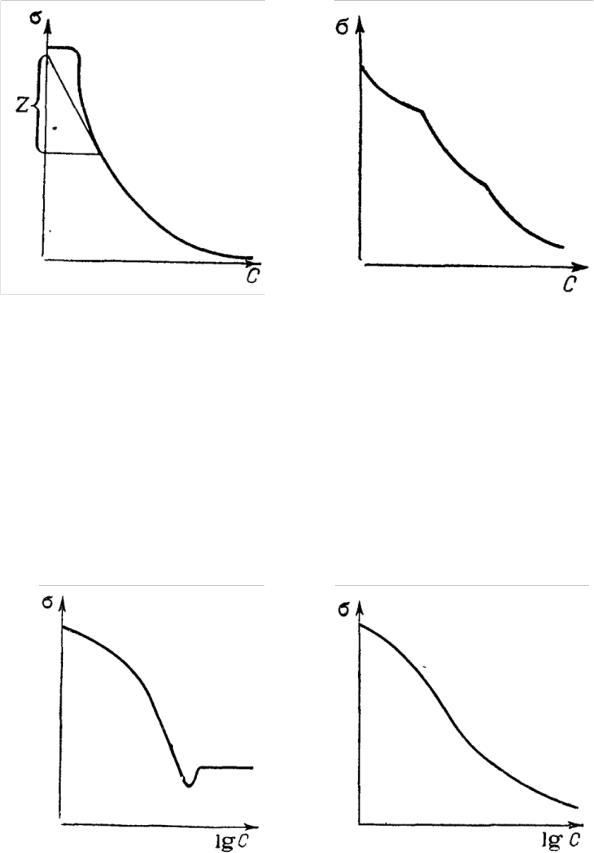
Рис. 14. Изотерма поверхностного |
Рис. 15. Изотерма поверхностного |
натяжения в широком интервале |
натяжения смеси ПАВ |
|
|
концентраций ПАВ |
|
При содержании в индивидуальном ПАВ небольшого количества примесей (как правило, тоже поверхностно-активных) изотерма отличается от показанной на рис. 15, лишь наличием небольшого минимума (рис. 16).
Если ПАВ содержит много примесей или представляет собой смесь веществ, то минимум исчезает, и изотерма в логарифмических координатах имеет вид плавной S-образной кривой, не разделенной четко на участки (рис. 17).
Рис. 16. Изотерма поверхностного |
Рис. 17. Изотерма поверхностного |
натяжения в присутствии |
натяжения смеси ПАВ |
небольшого количества примесей |
|
|
40 |
