ПАВ_курс лекций

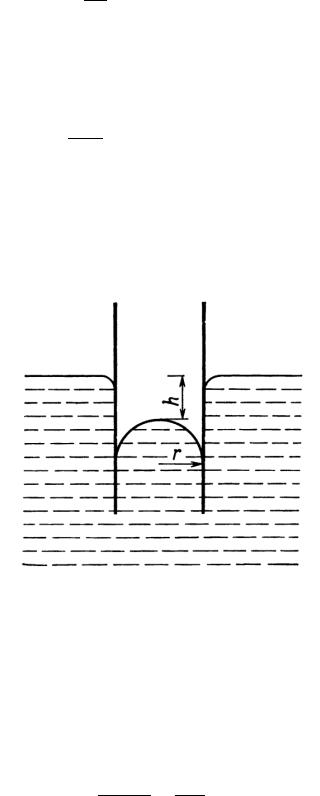
Поднятие (или опускание) жидкости в капилляре уравновешивается гидростатическим давлением:

(8)

где h – высота капиллярного поднятия (опускания); ρ – разность плотностей жидкой и газообразной фаз.

С другой стороны

(9)

где a – капиллярная постоянная.

При точной математической трактовке капиллярного поднятия необходимо принимать во внимание отклонение формы мениска от сферической (рис. 2).

Рис. 2. Схема опускания жидкости в капилляре

Башфорт и Адамс отработали метод, позволяющий учитывать несферичность мениска, который в дальнейшем был усовершенствован Сагденом. Обозначив за радиус кривизны величину b, Сагден ввел безразмерный параметр β, определяемый соотношением:

(10)

11

При идеальном смачивании и равенстве угла = 0, радиусы мениска и капилляра совпадают и равны r. Учесть отклонение мениска от сферического позволяет табл. 1 , составленная Сагденом и показывающая взаимосвязь между r/b и r/а.

Таблица 1

Поправочные коэффициенты на несферичность капли

Как пользоваться данной таблицей будет показано на конкретном примере в конце лекции.

12

Метод капиллярного поднятия имеет определенные достоинства. Его считают наиболее достоверным потому, что для его описания разработана довольно точная теория, и его можно осуществить экспериментально с контролируемой погрешностью. Для получения наиболее точных результатов необходимо соблюдать следующие условия:

-жидкость должна полностью смачивать капилляр; как правило, в большинстве случаев используются стеклянные капилляры, которые хорошо смачиваются большинством известных жидкостей;

-капилляр следует устанавливать строго вертикально; его радиус должен быть постоянен по всей длине, сечение капилляра может отклоняться от круга не более чем на несколько процентов;

-при использовании стеклянных капилляров щелочность жидкости не должна превышать некоторого предельного значения (чтобы не происходило выщелачивание стекла).

При соблюдении всех указанных условий погрешность метода составляет всего несколько сотых процента.

Метод максимального давления в пузырьке

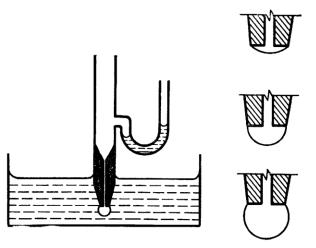
Данный метод также позволяет определять поверхностное натяжение жидкостей σж-газ и заключается в медленном выдувании пузырьков в исследуемую жидкость (рис. 3). Пузырьки выдувают инертным газом с помощью трубки, частично погруженной в жидкость. Как видно из рисунка, если радиус трубки не велик, то растущий пузырек представляет собой часть сферы. В данном случае также применимо уравнение Лапласа:

(11)

где r – радиус пузырька.

Радиус пузырька минимален, когда пузырек является точно полусферическим. В этот момент он равен радиусу трубки, и поскольку радиус пузырька минимален, то P достигает своего максимального значения. Такой вариант возможен только для очень узких трубок, значительные погрешности определения σ наблюдаются при r/а, равном 0,05.

Как и в случае капиллярного поднятия, Сагден рассчитал и протабулировал поправочные коэффициенты для данного метода, введя некоторую

13

постоянную Х = a2/h. Любому данному значению r/a соответствует значение r/X (табл. 2).

Рис. 3. Схема прибора для максимального давления в пузырьке

Точность определения по методу максимального давления в пузырьках достигает нескольких десятых процента. Скорость роста пузырьков должна составлять около 1/с. Таким образом, данный метод является квазидинамическим и характеризует натяжение свежеобразованных поверхностей жидкость-газ. Для стареющих поверхностей данный метод использовать нецелесообразно.

Таблица 2

Поправочные коэффициенты на несферичность для метода максимального давления в пузырьке

Как пользоваться данной таблицей будет показано на конкретном примере в конце лекции.

14

Метод взвешивания капель

Это довольно точный и наиболее распространенный лабораторный метод измерения межфазных натяжений на границах раздела σж-газ и σж-ж. Методика измерения заключается в следующем: на конце капилляра формируют капли жидкости, капающие в контейнер, заполненный другой жидкостью (в случае определения σж-ж) или в пустой контейнер (в случае определения σж-газ). Собирают и считают капающие капли до тех пор, пока можно будет достаточно точно определить их вес. Зная количество капель и их общую массу, можно определить объем и радиус одной капли.

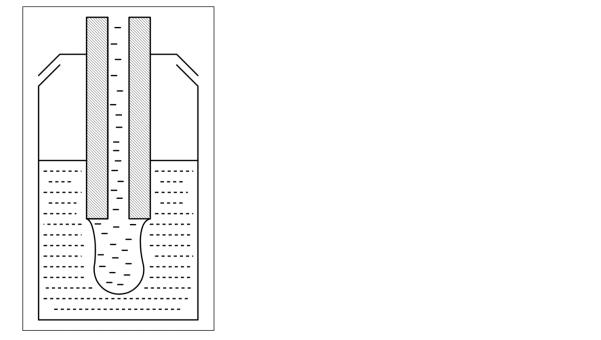
Остановимся подробнее на более сложном варианте – измерении σж-ж (рис. 4). Для дальнейшего расчета необходимо знать плотности жидкостей, а также радиус капилляра. При этом необходимо учитывать то, что если жидкость в капилляре смачивает его, то при расчете используется внешний радиус капилляра, если нет – внутренний. При подготовке эксперимента надо помнить о том, что в капилляре должна находиться жидкость с более высокой плотностью, а в контейнере-сборнике – жидкость с меньшей плотностью.

Рис. 4. Схема основного узла установки для метода веса-объема капли

При расчетах используют уравнение Тэйта, известное с 1864 года и называемое законом Тэйта:

(12)

15

где 2πr – длина окружности кончика капилляра; − межфазное натяжение; W – вес капли.

Закон Тэйта базируется на концепции о том, что максимальная сила, удерживающая каплю на кончике капилляра, равна межфазному (поверхностному) натяжению, умноженному на длину окружности кончика трубки.

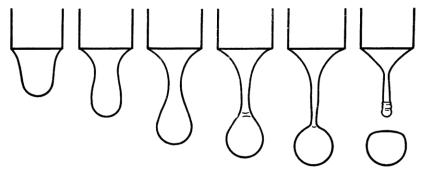
Фактически же на практике получают вес капли W’ , который меньше идеального рассчитанного. Причина этого становится понятной при помощи рис. 5. Вследствие механической нестабильности образующейся цилиндрической шейки капли фактически падает только часть капли, достигшая точки нестабильности, до 40% жидкости остается в капилляре.

Рис. 5. Деформация капли в методе веса-объема капли

Учитывая это, Гаркинс и Браун пришли к выводу, что фактический вес капли W’ можно рассчитать как:

(13)

где f − некоторый поправочный коэффициент, являющийся функцией от соотношения радиуса капилляра и объема капли, т.е. f = Ψ ( r/V1/3). Значения поправочного коэффициента в зависимости от указанного соотношения приведены в табл. 3.

Измерения рекомендуется проводить при значениях r/V1/3 от 0,6 до 1,2, когда коэффициент f меняется наиболее медленно. При использовании данного метода важно применять трубки с полированными концами, не содержащими каких-либо трещин и зазубрин. Капли должны формироваться медленно, если длительность роста капли составляет 1 мин, ошибка эксперимента близка к 0,2%. В целом, точность определения этим методом составляет от 0,1 до 0,3%.

16

Как пользоваться данной таблицей будет показано на конкретном примере ниже.

Метод отрыва кольца

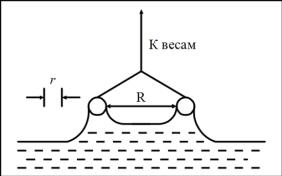
Данный метод позволяет определять поверхностное натяжение жидкостей σж-газ. Его автором считают Дю Ноя. Заключается он в следующем: определяется сила отрыва кольца или петли из проволоки от поверхности жидкости (рис. 6). При этом предполагается, что сила отрыва равна поверхностному натяжению, умноженному на периметр поверхности отрыва. Таким образом, для кольца, показанного на рис. 6, можно записать:

(14)

где Wк – вес кольца.

Рис. 6. Схема основного узла установки в методе отрыва кольца

17

Гаркинс и Джордэн показали, что это уравнение дает большую погрешность, и ввели коэффициент f, определяемый соотношением:

( )

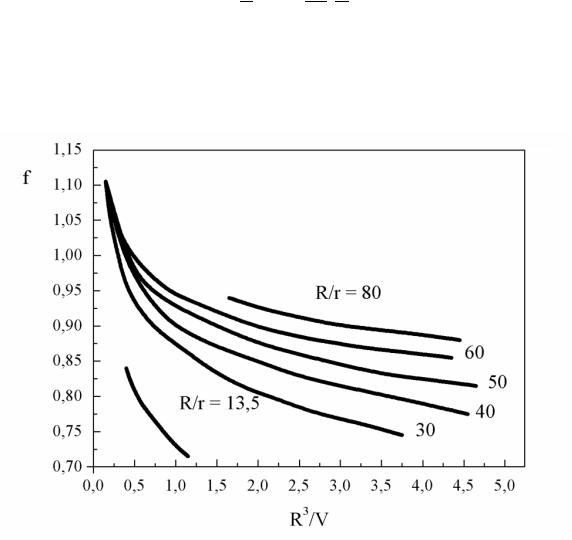
где p – идеальное поверхностное натяжение, рассчитанное по вышеприведенному уравнению без поправок, а V – объем мениска. Поправочные кривые для определения коэффициента f приведены на рис. 7.

Рис. 7. Поправочные кривые для метода отрыва кольца

Точность данного метода может быть достаточно высокой. Экспериментатор должен обратить внимание на следующие моменты. Перед опытом необходимо определять вес сухого кольца, обычно изготавливаемого из платины. Кольцо должно поддерживаться в горизонтальном положении (установлено, что отклонение от горизонтали на 1 дает погрешность в 0,5%, а при отклонении на 2,1 погрешность составляет 1,6%). Необходимо применять специальные меры предосторожности, чтобы исключить возмущение поверхности вблизи критической точки отрыва. Для удаления поверхностных загрязнений перед опытом кольцо прокаливают на горелке.

18

Чтобы обеспечить чистоту исследуемой поверхности, рекомендуется заполнять кювету доверху и затем сливать часть жидкости через край кюветы. Желательно, чтобы краевой угол был близок к нулю, иначе результаты окажутся заниженными. В некоторых случаях вместо платиновых можно использовать тефлоновые или полиэтиленовые кольца.

Рассмотрением данного метода завершается изучение жидкой поверхности раздела, однако нельзя забывать, что здесь рассмотрена только часть используемых на практике методов определения σж-газ и σж-ж. Существует еще множество других методов, описанных в специальной литературе.

Теперь рассмотрим два метода, позволяющих определять межфазные натяжения на границе σж-тв и поверхностные натяжения некоторых твердых тел σтв-газ.

2.2. Определение межфазного натяжения на границе жидкость-твердое (σж-тв)

Из общего курса коллоидной химии известно, что дисперсность существенно влияет на растворимость плохо растворимых частиц в различных растворителях. Это может быть описано с помощью известного также из общего курса коллоидной химии уравнения Кельвина:

(15)

где sr и s∞ − растворимость сферических микрочастиц и растворимость сферических макрочастиц, соответственно; rr – радиус микрочастицы. Из последнего уравнения видно, что с увеличением дисперсности растворимость растет, т.е. чем меньше частица, тем больше ее растворимость. Это уравнение лежит в основе метода определения межфазного натяжения на границе твердое – раствор (σж-тв). Экспериментально определяют растворимость твердых частиц в зависимости от дисперсности вещества и рассчитывают межфазное натяжение. Недостатки метода заключаются в сложности получения нескольких частиц одинакового размера, а также в том, что метод не позволяет учесть то, что у анизотропных кристаллических тел каждая грань имеет свое межфазное натяжение.

19

2.3. Определение поверхностного натяжения на границе твердое-газ (σтв-газ). Метод Цисманна

Как уже говорилось ранее, экспериментальное определение межфазных натяжений на жидкой границе раздела фаз не вызывает особых затруднений. Достаточно надежных методов определения поверхностного натяжения твердых тел нет. Для оценки этой величины используются расчетные или экспериментальные косвенные методы. В частности, для полимеров, одним из наиболее распространенных косвенных методов является метод, предложенный Цисманном.

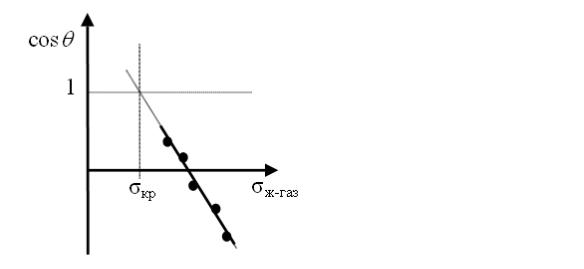
Суть данного метода заключается в определении критического поверхностного натяжения смачивания σкр. Эту величину находят по зависимости косинусов краевых углов натекания (cosθнт) от поверхностного натяжения жидкости (σж-газ). В качестве жидкости используются либо гомологи с различными величинами поверхностного натяжения (спирты, кислоты и пр.), либо растворы одного вещества с различными концентрациями и, соответственно, различными значениями σж-газ. Для многих твердых низкоэнергетических поверхностей при уменьшении поверхностного натяжения σж-газ, значения cosθнт линейно возрастают. Это позволяет определить значение σж-газ, при котором происходит полное смачивание твердой поверхности, экстраполируя зависимость cosθнт = f(σж-газ) до значения cosθнт=1. Это значение σж-газ и называют критическим натяжением смачивания (рис. 8).

Рис. 8. Определение σкр методом Цисманна

20