
ПАВ_курс лекций
.pdf
вода), либо обратных (вода-масло) эмульсий. Для некоторых соединений были выбраны условно числа ГЛБ, в частности, для олеата натрия –18; триэтаноламина –12 и для олеиновой кислоты –1. При этом предполагалось, что чем выше гидрофильность, тем выше ГЛБ.
Определение чисел ГЛБ по Гриффину проводят следующим способом. Готовят эмульсии из воды и стандартного масла (обычно гептана) с эмульгаторами из смеси ПАВ с известным и неизвестным значением ГЛБ. Эмульсии выдерживают 24 часа, затем определяют наиболее устойчивую эмульсию или фиксируют обращение эмульсии (переход прямой в обратную или наоборот) и рассчитывают ГЛБ исследуемого ПАВ, считая это свойство аддитивным по формуле:
(91)
где ГЛБсм – число ГЛБ смеси ПАВ, обеспечивающее получение устойчивой эмульсии стандартного масла; WA – количество эмульгатора А с известным ГЛБ - ГЛБА; WB – количество эмульгатора В с неизвестным ГЛБВ.
Проводя дальнейшие исследования, Гриффин на основании экспериментального определения стабилизации эмульсий предложил ряд эмпирических формул для расчета ГЛБ. Он установил, что отрицательные изменения чисел ГЛБ происходят при увеличении числа метиленовых групп в молекулах ПАВ, а при повышении числа гидрофильных групп ГЛБ увеличивается.
Так, в частности, ГЛБ можно рассчитать в некоторых случаях из данных по составу ПАВ. Например, для сложных эфиров жирных кислот и полиосновных спиртов можно использовать формулу:
( |
|
) |
(92) |
|
|
||
|
|
где S – число омыления эфира; А – кислотное число жирной кислоты.
Для расчета ГЛБ неиногенных ПАВ типа оксиэтилированных кислот Гриффином предложена следующая формула:
( |
) |
(93) |
|
|
|
|
61 |
|

где Е и Р – соответственно весовое содержание (мас. %) окиси этилена и углеводорода.
Если же ПАВ представляет собой оксиэтилированный алкилфенол или спирт, то для расчета ГЛБ можно использовать следующее соотношение:
(94)
Учитывая, что |
|
, где MR – молекулярная масса углеводо- |
|
родной части ПАВ; 44 – молекулярная масса 1 группы окиси этилена; ne – степень оксиэтилирования.
1.2. Метод Дэвиса
Несмотря на свое широкое применение, метод Гриффина имеет ряд недостатков и никак не обоснован с физико-химической точки зрения. Дэвис предпринял попытку связать числа ГЛБ с изменением какого-либо свойства растворов ПАВ. Он пришел к выводу о том, что величина ГЛБ складывается аддитивно из инкрементов групп, входящих в молекулу ПАВ. Дэвис вычислил групповые числа (инкременты) для различных полярных и неполярных групп, комбинируя которые можно рассчитать ГЛБ всей молекулы ПАВ по уравнению:
∑( ) ∑( ) |
(95) |
|
где Σ(ГЛБ)Г – сумма чисел ГЛБ всех гидрофильных групп; Σ(ГЛБ)Л – сумма чисел ГЛБ всех липофильных групп. Для большинства функциональных групп значения чисел ГЛБ приведены в табл. 9.
В дальнейшем Дэвис попытался дать научное обоснование предложенному им методу. При изучении устойчивости эмульсий, стабилизированных различными ПАВ, он ввел кинетический параметр для характеристики ГЛБ, а затем и термодинамический параметр, связав его с коэффи-
62
циентом распределения ПАВ между водой и углеводородом. В результате было предложено уравнение:
( |
в |
) |
(96) |
|
|
где cв и со – концентрация ПАВ в водной и углеводородной (масляной) фазах.
|
|
Таблица 9 |
|
Групповые числа ГЛБ |
|
||
|
|
|
|
Гидрофильные группы |
ГЛБ |
Липофильные группы |
ГЛБ |
|
|
|
|
-SO4Na |
38,7 |
-CH2- |
−0,475 |
|
|
|
|
-SO4К |
39,0 |
|
|
|
|
|
|
-COOK |
21,1 |
-CH3 |
−0,475 |
|
|
|
|
-COONa |
19,1 |
-CH= |
−0,475 |
|
|
|
|
Сульфонат |
11,0 |
-(CH2-CH2-CH2-O-) |
−0,15 |
|
|
|
|
-N (третичный амин) |
9,4 |
|
|
|
|
|
|
Сложный эфир |
6,8 |
-(CH2-CH2-CH2-CH2-O-) |
−0,62 |
(сорбитановое кольцо) |
|
|
|
|
|
|
|
Сложный эфир (свободный) |
2,4 |
|
|
|
|
|
|
-COOH |
2,1 |
-CF2 |
−0,87 |
-OH (свободный) |
1,9 |
-CF3 |
−0,87 |
|
|
|
|
-O- |
1,3 |
|
|
|
|
|
|
-OH (сорбитановое кольцо) |
0,5 |
|
|
|
|
|
|
-N (четвертичный амин) |
9,4 |
|
|
|
|
|
|
-(CH2-CH2-O-) |
0,33 |
|
|
|
|
|
|
Позже термодинамическое обоснование этой формулы дал А.И. Русанов. Он связал ГЛБ с работой перехода (WВ-О) элементов молекул ПАВ из водной фазы в углеводородную с учетом того, что при низких концентрациях можно пренебречь отклонением соответствующих растворов от идеальности.
Учитывая, что для 1 моль ПАВ WВ-О = RT ln (cв/со), можно записать:
63

(97)
В таком случае можно говорить о том, что групповые числа Дэвиса представляют собой парциальные значения работы переноса моля соответствующих групп из водной среды в углеводородную.
1.3. Метод Лин
Развивая дальнейшие представления о ГЛБ и связывая их с различными свойствами растворов ПАВ, Лин с сотрудниками сравнили групповые числа Дэвиса со свободной энергией переноса молекул ПАВ из объема фаз на поверхность. При этом предполагалось, что такая работа адсорбции не будет сильно отличаться от работы мицеллообразования, т.е. можно использовать уравнение, связывающее критическую концентрацию мицеллообразования (ККМ) с числом метиленовых групп (nc) в липофильной цепи при постоянстве гидрофильной группы:
(98)
где скр = ККМ; А и В – константы, имеющие физический смысл инкремента свободной энергии мицеллообразования полярной и метиленовой групп, соответственно.
Для неиногенных ПАВ наблюдается аналогичная зависимость ККМ от степени оксиэтилирования ne при фиксированной гидрофобной части молекулы:
(99)
На основе этих уравнений несколько позже были получены соотношения, связывающие числа ГЛБ, рассчитанные по методам Гриффина и Дэвиса, с величинами ККМ ПАВ. Так, взаимосвязь между величиной ККМ и ГЛБ по Дэвису определяется следующим линейным уравнением:
( ви ) |
(100) |
где a и b – константы, некоторые из которых приведены в табл. 10.
64
|
|
|
Таблица 10 |
Взаимосвязь между ККМ и ГЛБ |
|||
|
|
|
|
Гомологический ряд |
a |
b |
Единица выражения cкр |
CnH2n+1(OC2H4)nOSO3Na |
−37,14 |
0,866 |
моль/л |
|
|
|
|
CnH2n+1COOK |
−16,33 |
0,718 |
моль/л |
CnH2n+1COONa |
−15,23 |
0,611 |
моль/л |
|
|
|
|
CnH2n+1SO4Na |
−26,96 |
0,621 |
моль/л |
|
|
|
|
CnH2n+1SO3Na |
−8,28 |
0,510 |
моль/л |
|
|
|
|
CnF2n+1COOH |
−3,48 |
0,510 |
моль/л |
|
|
|
|
CnF2n+1COOK |
−16,155 |
0,658 |
моль/л |
CnF2n+1COONa |
−16,287 |
0,743 |
моль/л |
|
|
|
|
C12H35(OC2H4)nOH |
−2,13 |
0,093 |
г/л |
|
|
|
|
C9H19C6H4(OC2H4)nOH |
−1,903 |
0,132 |
г/л |
|
|
|
|
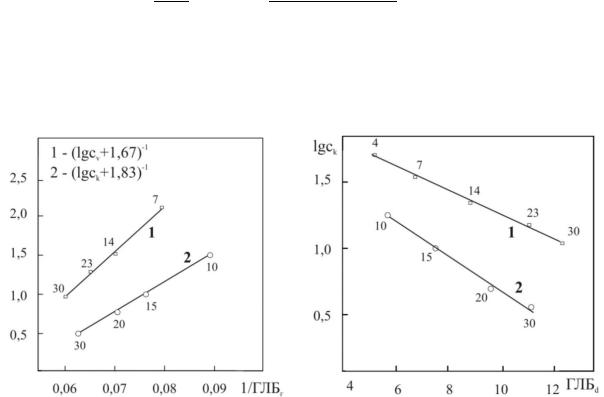
Взаимосвязь между ККМ и ГЛБ по Гриффину отражает такое уравнение:
(101)
( )
На рис. 35 и 36 приведены примеры взаимосвязи между ККМ и ГЛБ по Гриффину и Дэвису, соответственно.
Рис. 35. Взаимосвязь между ККМ |
Рис. 36. Взаимосвязь между ККМ |
и ГЛБ по Гриффину |
и ГЛБ по Дэвису |
|
65 |
1.4.Метод Шиноды
Вданном методе расчета ГЛБ предпринята попытка установления взаимосвязи между ГЛБ и температурой Крафта для ионных ПАВ и точкой помутнения для неионных ПАВ.
Известно, что свойства растворов ПАВ изменяются при изменении температуры. Изменения растворимости отражаются в изменениях поверхностной активности, величинах ККМ, и, в конечном итоге, и в числах ГЛБ. Изменение ГЛБ при повышении температуры способно привести к тому, что в результате нагревания может произойти обращение фаз стабилизируемой тем или иным ПАВ эмульсии. Шинода предложил рассматривать взаимосвязь между температурой инверсией фаз (ТИФ) и ГЛБ. При этом было обнаружено, что эта зависимость часто носит экстремальный характер.
Вчастности, для водных растворов гомологических рядов неионных ПАВ, различающихся по степени оксиэтилирования, но имеющих одиноковый углеводородный радикал, справедливо следующее уравнение:
( ) ( ) (102)
где Тп ( С) – температура помутнения. Значения констант а, b и с приведены в табл. 11.
|
|
|
|
Таблица 11 |
Взаимосвязь между Тп и величинами ГЛБ |
|
|||
|
|
|
|
|
Гомологический ряд ПАВ. |
|
Константы уравнения |
||
Нормальное распределение |
|
|
|
|
a |
|
b |
c |
|
по степени оксиэтилирования |
|
|
|
|
|
|
|
|
|
C9H19C6H4(OC2H4)nOH |
−874,6 |
|
114,65 |
−3,323 |
|
|
|
|
|
C8H17C6H4(OC2H4)nOH |
−1880,0 |
|
261,60 |
−8,779 |
|
|
|
|
|
C12H25(OC2H4)nOH |
−197,5 |
|
20,41 |
0 |
|
|
|
|
|
Гомогенные |
|
|
|
|
|
|
|
|
|
C12H25(OC2H4)nOH |
−323,7 |
|
43,098 |
−0,9474 |
66

1.5.Метод Круглякова−Корецкого
Вданном случае авторы предложили некоторую альтернативу гидро- фильно-липофильному балансу, назвав новую характеристику гидрофиль- но-олеофильным соотношением (ГОС). Эта характеристика выражается через отношение работ адсорбции молекулярно-растворенного ПАВ из водной и углеводородной фаз на их общую границу раздела.
(103)
Такая оценка имеет строгий физический смысл, основанный на термодинамических параметрах системы. Метод основан на использовании одного из основных свойств ПАВ – адсорбционной способности на границе раздела фаз и учитывает относительную автономность гетерополярных частей в молекуле.
Несколько позже В.В. Свиридов предложил определять значения ГОС через отношение работ мицеллообразования в углеводородной G0Om и водной G0Вm фазах:
(104)
Это уравнение нашло широкое применение, поскольку определение ККМ во многих случаях проблем не вызывает.
ГОС можно характеризовать и коэффициентом распределения Кр, который определяют по равновесным концентрациям вещества, выраженным в мольных долях, растворенного в обеих несмешивающихся фазах, одна из которых – вода. Для расчета коэффициента распределения предложено следующее уравнение:
(105)
где ао, aB – активности насыщенного молекулярного раствора ПАВ в углеводородной жидкости и воде, соответственно; cko и ckB – критические концентрации мицеллообразования в углеводородной и водной фазах.
(106)
67
где сk – критическая концентрация мицеллообразования, выраженная в мольных долях.
С другой стороны,
(107)
где nc – количество метиленовых групп в углеводородном радикале молекулы ПАВ.
При использовании данного метода при определении ГОС в качестве углеводородной среды предпочтительно, как и в методу Гриффина, использовать гептан.
В качестве заключения к этому разделу, посвященному расчету чисел ГЛБ, необходимо обратить внимание на то, что числа ГЛБ, определенные разными методами, могут весьма существенно отличаться друг от друга.
Примеры решения типовых задач
Задача 1. Используя метод Дэвиса, рассчитайте числа ГЛБ для следующих ПАВ: додецилсульфат натрия, бутиловый спирт и трибутилацетат.
Додецилсульфат натрия: С12Н25ОSO3Na
ГЛБ = (−0,475) 12 + 38,7 +7 = 40
Бутиловый спирт: С4Н9ОН ГЛБ = (−0,475) 4 + 1,9 + 7 = 7
Трибутилацетат: СН3СООС4Н9
ГЛБ = (−0,475) 5 + 2,4 + 7 = 7,025 7
2. Параметр упаковки молекул ПАВ. Расчет параметров упаковки
Помимо чисел ГЛБ и величин ККМ, есть еще одна величина, характеризующая состояние ПАВ в жидкой фазе. Данная величина называется параметром упаковки и в большинстве литературных источников обозначается Ns. Параметр упаковки является безразмерной величиной отношения объема гидрофобной части ПАВ (v) к длине гидрофобной части ПАВ (l) и площади концевой полярной группы (so). Таким образом:
68

(108)
(при расчетах параметра упаковки молекул ПАВ, содержащих два и более гидрофобных радикала, необходимо учитывать, что объем занимает каждый из радикалов, в то время как их длину считают постоянно независимо от их количества).
Параметры объема и длины радикалов могут быть достаточно точно оценены по данным рентгенографических исследований различных гомологических рядов ПАВ. Анализ насыщенных углеводородных цепей дает оценку гидрофобного объема в нм3:
( |
) |
(109) |
где l отвечает полностью развернутой цепи в трансконформации, нм. Оценка величины so более затруднительна, поскольку этот параметр
очень сильно зависит от ионной силы среды и величины адсорбции противоиона (в случае ионных ПАВ). Адсорбционная способность противоиона в значительной степени влияет на силы межмолекулярного отталкивания концевых головок, что сильно сказывается на величине so.
Параметр упаковки используется для описания поведения ПАВ в жидкой фазе и дает возможность предположить, какого вида структуры может образовывать то или иное ПАВ в растворе в зависимости от его строения. Одним из первых данный параметр привел в своих работах Израелошвили. Так, каждому интервалу значений Ns соответствуют определенные структуры, образованные различными ПАВ (см. рис. 37).
Так, при Ns < 1/3 критической формой упаковки является конус. Самоассоциация таких конусов приводит к образованию сфероидальных мицеллярных структур. ПАВ, образующие такие структуры, состоят, как правило, из одного углеводородного радикала и достаточно большой полярной головки (например, додецилсульфат натрия).
Когда 1/3 < Ns < 1/2 критическая форма упаковки представляет собой усеченный конус. Подобные конусы могут ассоциировать с образованием стержнеобразных структур, таких как цилиндрические мицеллы (например, цетилтриметиламмонийбромид).
69

Конус Ns < 1/3
Сферические и эллипсоидальные мицеллы
Усеченный конус |
Цилиндрические и |
1/3 < Ns < 1/2 |
стержнеобразные мицеллы |
Усеченный конус
Полости и бислои
1/2 < Ns < 1
Цилиндр
Бислои
Ns ≈ 1
Перевернутый |
Обращенные мицеллы |
усеченный конус Ns > 1 |
(сферические и цилиндрические) |
Рис. 37. Параметр упаковки и геометрия структур
Крайне усеченный конус возможен при 1/2 < Ns < 1 и тогда возможно образование подвижных бислоев, подобных полостям в липосомах. Такие структуры могут образовывать аэрозоль ОТ (АОТ) или лецитин.
Цилиндрические критические формы упаковок с условием Ns 1 дают плоские бислойные ассоциаты. При Ns 1 происходит образование перевернутого усеченного конуса и обратных сферических мицелл.
При оценке величины Ns необходимо учитывать и тот факт, что одно и то же ПАВ в различных растворителях может формировать структуры различного типа. Так, как уже упоминалось, в воде АОТ формирует бислои, тогда как в гексане он образует обратные сферические мицеллы.
Тем не менее, существуют некоторые обобщения, связывающие величину параметра Ns со строением молекулы ПАВ. В частности, одноцепные ПАВ склонны к формированию регулярных или прямых сферических
70
