книги / 639

REactor SIMulations), предназначенного для полномасштабного моделирования реакторов.

Рис. 2. Фрагмент тканого композита с искривленными волокнами

На рис. 2 представлен фрагмент слоя тканого композита с коэффициентами армирования α1 =α3 =0,14 вдоль утка и основы соответственно.

2. Краевая задача

Для простоты будем предполагать, что волокна и матрица слоя модельного тканого композита изотропные, линейно упругие, не изменяющие геометрию, взаимное расположение и тип симметрии при нагружении. Тогда компоненты тензора напряжений σij (r) удовлетво-

ряют уравнениям равновесия в отсутствии массовых сил

а компоненты тензора малых деформаций εij (r) связаны с компонентами вектора перемещений ui (r) геометрическими соотношениями Коши

Для описания геометрии слоя тканого композита введем единичную кусочно-однородную индикаторную функцию радиус-вектора r ,

31

которая принимает значение 1, если точка принадлежит нити основы или утка, и значение 0, если эта точка принадлежит матрице. Тогда определяющие соотношения могут быть записаны следующим образом:

В уравнениях (3) верхними индексами f и m отмечены матери-

альные коэффициенты, относящиеся к волокнам и матрице соответственно.

Краевая задача (1)–(3) дополняется граничными условиями

u1 (r)Γ2 =u10 , u3 (r)Γ1 =u30 , u1 (r)Γ4 =u3 (r)Γ3 =u3 (r)Γ5 =u2 (r)Γ6 =0 ,(4)

σ12 (r)Γ4 =σ13 (r)Γ4 =σ13 (r)Γ3 =σ23 (r)Γ3 =0 , σ12 (r)Γ5 =σ13 (r)Γ5 =σ12 (r)Γ6 =σ13 (r)Γ6 =0 ,

обеспечивающими заданное макрооднородное неравнокомпонентное деформирование вплоскости слоя, и условиямиидеального сопряжения

на границах раздела фаз (рис. 2). Внутренняя пора моделируется исключением из рассмотрения локального объема матрицы. Точки образовавшейся внутренней поверхности Γ8 не имеют ограничения на пе-

ремещения, а сама поверхность свободна от напряжений:

3. Коэффициенты концентрации напряжений

Численное решение краевой задачи (1)–(3) с граничными условиями (4)–(6) методом конечных элементов будем проводить в некоммерческом пакете Code-Aster, входящем в состав платформы SALOME–MECA. Этот пакет был разработан и сертифицирован специально для французской энергетической отрасли и предназначен для задач механики сплошных сред, термо- и гидродинамики, акустики

имагнетизма, выполнения расчетов для строительных конструкций

исооружений.

32

Дискретизация фрагмента проводилась на 16-узловые тетераэдральные и 20-узловые гексаэдральные изопараметрические элементы. Степень дискретизации выбиралась таким образом, чтобы полученные значения структурных перемещений, деформаций и напряжений в слое тканого композита без локальных дефектов и с несовершенствами ни качественно, ни количественно не изменялись при уменьшении характерных размеров конечных элементов. Этим условиям удовлетворяют сетки, содержащие 298255 и 287924 16-узловых тетраэдральных элементов для композита идеальной периодической структуры и материала с внутренней порой. Количество 20-узловых гексагональных элементов для двух рассматриваемых случаев было одинаково и равнялось 77760. Результаты численного решения показали, что при равнокомпонентном двухосном растяжении распределение искомых полей напряжений, деформаций и перемещений в слое материала идеальной структуры удовлетворяет условиям симметрии и периодичности геометрической модели и приложенной внешней нагрузке. Это свидетельствует о корректности полученного численного решения.

Рис. 3. Поля интенсивности напряжений фрагмента тканого композита

На рис. 3 показаны распределения интенсивностей напряжений в волокнах основы и утка при равнокомпонентном двухосном однородном деформировании слоя модельного тканого композита, имеющего идеальную периодическую структуру, в собственной плоскости.

Модуль Юнга и коэффициент Пуассона волокон E f =280 ГПа и ν f =0,20 ГПа соответствовали данным работы [3]. Упругие модули поликристаллической матрицы были выбраны следующими:

Em =0,28 ГПа и νm =0,40 .

33

Рис. 4. Распределение коэффициентов концентрации интенсивности напряжений в слое тканого композита с локальным дефектом в виде внутренней поры

При двухосном равнокомпонентном растяжении безразмерные коэффициенты Kσij =σij (r)σijper (r), определяемые отношением ос-

редненных компонент тензора напряжений в слое модельного тканого композита с локальным дефектом и соответствующих осредненных компонент в слое материала идеальной периодической структуры,

ние локальных коэффициентов, рассчитанных как соответствующее отношение интенсивностей напряжений. Расположение областей, в которых интенсивность напряжений достигает максимальных значений в местах, где искривленные волокна основы или утка имеют наибольшую кривизну, строго периодично. Исключение составляет область, расположенная вблизи локального дефекта, где интенсивность напряжений в 1,25 раза превышает соответствующее значение, определенное для композита идеальной периодической структуры. Обратим внимание на то, что наибольший вклад в коэффициенты концентрации вносят касательные составляющие тензора напряжений σ12 и σ23 . Значе-

ния этих напряжений более чем в четыре раза превышают напряжения в идеальной периодической структуре. Поэтому для повышения способности тканых композитов сопротивляться внешнему силовому воз-

34

действию желательно предусмотреть в технологическом процессе операции, обеспечивающие проникновение связующего в полости технологических локальных дефектов, а также дополнительную пропитку связующим, доуплотнение и карбонизацию, досаждение поликристаллической матрицы из газовой фазы в случае, если в результате ультразвукового контроля готового изделия обнаруживаются внутренняя пористость. В противном случае возможно развитие дефектов и последующее разрушение материала матрицы по механизмам сдвигов.

Заключение

На основе построенной модели слоя тканого композита с искривленными волокнами и поликристаллической матрицей определены коэффициенты концентрации напряжений, вызванные наличием технологического локального дефекта в виде закрытой поры при двухосном равнокомпонентном растяжении, определены механизмы, инициирующие разрушение матрицы.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант РФФИ–Урал № 11–01–96033).

Библиографический список

1.Суровикин В.Ф., Суровикин Ю.В., Цеханович М.С. Новые направления в технологи получения углерод-углеродных материалов. Применение углерод-углеродных материалов // Рос. хим. ж-л. (Ж-л. Рос. хим.

об.-ва им. Д.И. Менделеева). – 2007. – Т. LI, № 4. – С. 111–118.

2.Иманкулова А.С. Текстильные композиты. – Бишкек, 2005. –

152 с.

3.Конструкционные особенности материалов, армированных высокомодульными волокнами / Ю.М. Тарнопольский, А.В. Розе, И.Г. Жигун, Г.М. Гуняев // Механика полимеров. – 1971. – № 4. – С. 676–685.

References

1. Surovikin V.F., Surovikin Yu.V., Tsekhanovich M.S. New ways in the manufacturing technology of carbon-carbon materials. The use of car- bon-carbon materials [Novye napravleniya v technologii polucheniya uglerod-uglerodnych materialov. Primeneniye uglerod-uglerodnych materialov] // Russian Chemical Journal (Journal of Mendeleyev’s Russian Chemical Society). 2007. Vol. LI, No. 4. P. 111–118.

35

2.Imankulova A.S. Textile composites [Textilnye composity] – Bishkek: MOK, 2005. 152 p.

3.Tarnopolskiy Yu.M., Roze A.V., Zhigun I.G., Gunyaev G.M. Structural particularities of high-modulus fiber reinforced materials [Konstrukscionnye osobennosti materialov, armirovannych vysocomodulnymi voloknami] // Polymer mechanics. 1971. No. 4. P. 676–685.

Об авторах

Дедков Денис Владимирович (Пермь, Россия) – аспирант ка-

федры механики композиционных материалов и конструкций, Пермского национального исследовательского университета (614990,

г. Пермь, Комсомольский пр-т, 29, e-mail: denis.v.dedkov@gmail.com).

Зайцев Алексей Вячеславович (Пермь, Россия) – кандидат фи-

зико-математических наук, доцент кафедры механики композиционных материалов и конструкций Пермского национального исследовательского университета (614990, г. Пермь, Комсомольский пр-т, 29, e-mail: zav@pstu.ru).

Ташкинов Анатолий Александрович (Пермь, Россия) – доктор физико-математических наук, профессор, ректор Пермского национального исследовательского университета (614990, г. Пермь, Комсо-

мольский пр-т, 29, e-mail: rector@pstu.ru.

About the authors

Dedkov Denis Vladimirovich (Perm, Russia) – Postgraduate Student of the Department of Mechanics of Composite Materials and Structures, State National Research Polytechnical University of Perm (614990, 29, Komsomolsky Ave., Perm, Russia, e-mail: denis.v.dedkov@gmail.com).

Zaitsev Alexey Vyacheslavovich (Perm, Russia) – PhD in Physical and Mathematical Sciences, Associate Professor of the Department of Mechanics of Composite Materials and Structures, State National Research Polytechnical University of Perm (614990, 29, Komsomolsky Ave., Perm, Russia, e-mail: zav@pstu.ru).

Tashkinov Anatoly Alexandrovich (Perm, Russia) – Doctor of Physical and Mathematical Sciences, Rector of State National Research Polytechnical University of Perm (614990, 29, Komsomolsky Ave., Perm, Russia, e-mail: rector@pstu.ru ).

Получено 28.10.2011

36

УДК 593.3

А.В. Зайцев, Ю.В. Соколкин, А.А. Фукалов

Пермский национальный исследовательский политехнический университет, Пермь, Россия

ЭФФЕКТИВНЫЕ МОДУЛИ ОБЪЕМНОГО СЖАТИЯ ПРИ ПЛОСКОЙ ДЕФОРМАЦИИ ДВУХФАЗНЫХ ОДНОНАПРАВЛЕННО АРМИРОВАННЫХ КОМПОЗИТОВ С АНИЗОТРОПНЫМИ ПОЛЫМИ И СПЛОШНЫМИ ВОЛОКНАМИ

В рамках полидисперсных моделей механики композитов получены аналитические выражения для эффективных модулей объемного сжатия однонаправленно армированных материалов, трансверсально-изотропные матрицы которых армированы трансверсально-изотропными полыми или сплошными цилиндрическими волокнами различного диаметра, а на межфазных поверхностях выполняются условия идеального сопряжения. На основе полученных решений спрогнозированы эффективные модули объемного сжатия трабекулярной костной ткани и проанализировано изменение этих характеристик с биологическим возрастом человека при различной объемной пористости.

Ключевые слова: полидисперсная модель, однонаправленно армированный композит, анизотропные полые и сплошные цилиндрические волокна, идеальное сопряжение на межфазной поверхности, эффективные модули объемного сжатия при плоской деформации, трабекулярная костная ткань, влияние пористости и биологического возраста.

A.V. Zaitsev, Yu.V. Sokolkin, A.A. Fukalov

State National Research Polytechnical University of Perm, Perm, Russia

EFFECTIVE BULK MODULI UNDER PLAIN STRAIN

TO TWO-PHASE UNIDIRECTIONAL COMPOSITES REINFORCED BY ANISOTROPIC HOLLOW AND SOLID FIBERS

Applying polydisperse approximation the new exact analytical relationships for the effective bulk modules under plane strain are obtained for anisotropic trabecular bones taking into account biological age and a porosity. The forecasted changing of bulk modules under plane strain deals with age adaptation of bone’s structures. This is a basis for formulating the new methods of the warning and medical treatment of fractures, the complexes of gymnastic exercises, and individual selection of loading modes for akinetic patients.

Key words: polydispersible approximation, one-direction reinforced composite, anisotropic empty and solid cylindrical fibre, ideal coupling on contact surface, effective bulk modules under plane strain, trabecular bones, influence of porosity and biological age.

37

Полидисперсные модели механики композитов дают хорошие инженерные оценки для эффективных упругих модулей, если армирующими элементами являются бесконечно протяженные цилиндрические соосные круглые в поперечном сечении волокна, размещенные в изотропной матрице [1]. Однако использование этих моделей в случаях, если изотропная (эпоксидная или алюминиевая) матрица армирована анизотропными углеродными, органическими или природными волокнами или сама матрица анизотропна (керамическая или поликристаллическая), приводит к завышенным значениям эффективных упругих модулей. Поэтому учет анизотропии является одним из способов «редукции» или более адекватного описания экспериментальных данных для материалов, физико-механические свойства фаз которых не являются изотропными [2].

Еще одним примером материалов, которые могут рассматриваться среди возможных приложений, являются биологические костные ткани, состоящие из высокомодульных и высокопрочных неорганических волокон из кристаллов гидроксилапатита и матрицы в виде органических и коллагеновых волокон (создают монолитность строения). Аморфными органическими и минеральными веществами, которые также присутствуют в костной ткани в объеме 1 %, при прогнозировании эффективных упругих модулей можно пренебречь [3]. Предполагая, что волокна из кристаллов гидроксилапатита и коллагеновые волокна образуют непрерывные нити диаметром до 45 Å, расположенные вдоль продольной оси кости, будем считать, что костная ткань является трансверсально-изотропной средой. Это предположение не входит в противоречие с выводами авторов [4]. Несмотря на то, что на основе обработки экспериментальных результатов, полученных для образцов из отдельных зон поперечного сечения диафизарного отдела большой берцовой кости, делается вывод об ортогональной анизотропии материала, различие в модулях нормальной упругости в окружном и радиальном направлениях не превосходит 7,5–8,0 %.

Принимая гипотезы полидисперсных моделей [1], рассмотрим двухфазный композит, линейно-упругая однородная трансверсальноизотропная матрица которого армирована сплошными или полыми соосными трансверсально-изотропными круглыми в поперечном сечении волокнами различного диаметра. Будем считать, что каждое цилиндрическое волокно произвольного радиуса RA , окруженное слоем мат-

38

рицы толщиной RB − RA , является составным армирующим элементом, для которого отношения c = RARB и h = R0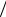RА (в случае полого ар-

мирующего элемента) являются постоянными величинами. Кроме того, будем предполагать, что волокна, матрица и составной армирующий элемент не изменяют тип упругой симметрии при нагружении, имеют ось симметрии бесконечного порядка, совпадающую с осью z цилиндрической ортогональной системы координат r , θ и z .

Рассмотрим произвольный бесконечно протяженный составной армирующий элемент, находящийся в плоскодеформированном состоянии, на внешней боковой цилиндрической поверхности которого задано равномерно распределенное радиальное давление p:

Используя точные аналитические решения задач Ламе о равновесии толстостенных трансверсально-изотропных цилиндров [5], запи-

Здесь и далее все величины, относящиеся к волокнам и матрице, будут отмечены индексами F и M соответственно.

Для композита со сплошными волокнами в уравнениях (3) исключим слагаемые, содержащие BI . Наличие этих слагаемых в решении приведет к сингулярности радиальных перемещений и напряжений в точках, принадлежащих оси симметрии армирующих элементов:

Содержащиеся в равенствах (3)–(5) константы определяются модулями Юнга EM , E%M , EF , E%F и коэффициентами Пуассона υM , υ%M , υF и υ%F материалов матрицы и волокон:

Ограничимся наиболее простым случаем, когда на межфазной поверхности композита выполняются условия идеального сопряжения

а внутренняя поверхность полых цилиндрических включений свободна от напряжений,

Из решения системы линейных алгебраических уравнений, которая получается при подстановке (4) и (5) в равенства (1) и условия (6), определяем константы интегрирования:

HC = K4 (K1 − K3)c2 + K3 (K1 + K4)

для композита, армированного сплошными цилиндрическими волокнами. В случае когда волокна полые, записать систему алгебраических уравнений и решить ее относительно неизвестных постоянных

40