
V [Cт A |
тCт (A |
т)2Cт (A |
т)n 1Cт] |
, |
(6.35) |
|
|
|
n mn |
|
|
имеющей n строк и mn столбцов. Здесь знак «т» обозначает операцию транспонирования матрицы. Критерий наблюдаемости формулируется следующим образом. Размерность n1 наблюдаемой части равна рангу матрицы V. Система является полностью наблюдаемой, если ранг матрицы V равен n.
При n1 n система полностью наблюдаема, при 0 n1 n – не полностью наблюдаема и при n1 0 – полностью ненаблюдаема.
Приведем простейшие примеры определения управляемости системы.
Пример 6.5. Система описывается уравнениями: x1 x2;
x2 x1 u.
В этом примере имеем (n 2, k 1):
0 |
1 |
|
|
0 |
|
|
|
|
|
1 |
|
A |
; |
|
B ; |
|
AB . |
||||||
1 |
0 |
|
|
1 |
|
|
|
|
|
0 |
|
Следовательно, |
0 |
1 |
|
|
|
0 |
1 |
|
|||
U B AB |
detU |
1 0, |
|||||||||
|
|
; |
1 |
0 |
|||||||
|
1 |
0 |
|
|
|
|
|||||
данная система полностью управляема. |
|
|
|
|
|
|
|||||
Пример 6.6. Система имеет вид: |
|
|
|
|
|
|
|||||
|
x1 x1 x2 u; |
|
|
|
|
||||||
Здесь имеем (n 2, k 1): |
x2 |
0. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
1 |
1 |
|
|
1 |
|
|
|
|
1 |
||
A |
; |
|
B ; |
|
AB . |
||||||
0 |
0 |
|
|
0 |
|
|
|
|
0 |
||
Получаем |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
detU |
|
1 |
1 |
|
0. |
|||
|
|
|
|||||||||
U |
; |
|
0 |
0 |
|
||||||
0 |
0 |
|
|
|
|
|
|
|
|||
Ранг этой матрицы r 1, т. е. r n – система не управляема. Приведем простейшие примеры определения наблюдаемости
системы.
138
Пример 6.7. Система описывается уравнениями:
|
|
x1 x2; |
|
|
|
|
|
|
||
|
|
x2 |
u; |
|
|
|
|
|
|
|
|
|
y x1. |
|
|
|
|
|
|
||
Здесь имеем (n 2, m 1): |
|
|
|
|
|
|
|
|
||
0 |
1 |
C 1 |
0; AтCт |
|
|
0 |
||||
A |
; |
|
. |
|||||||
0 |
0 |
|
|
|
|
|
|
1 |
||
Тогда матрица V получает вид |
|
|
|
|
|
|
|
|||
|
|
1 |
0 |
|
detV |
|
0 |
1 |
|
1, |
|
|
|
|
|
||||||
V Cт AтCт |
; |
|
1 |
0 |
|
|||||
|
|
0 |
1 |
|
|
|
|
|
||
ранг ее равен двум. Следовательно, данная система полностью наблюдаема. Действительно, если измерена величинаx1, то по первому уравнению системы определяется и x2.
Пример 6.8. Система задана уравнениями:
|
|
|
x1 x2; |
|
|
||
|
|
|
x2 |
u; |
|
|
|
|
|
|
y x2. |
1 . Следовательно, |
|||
Теперь изменилось только C 0 |
|||||||
Cт |
0 |
AтCт |
0 |
V |
0 |
0 |
detV 0. |
; |
; |
|
; |
||||
|
1 |
|
0 |
|
1 |
0 |
|
Система не является полностью наблюдаемой. Действительно, здесь измеряется величина x2, т. е. скорость изменения величины x1. Поэтому значение самой величины x1 остается неопределенным.
В общем случае динамическая система может содержать четыре части (рис. 6.7):
1)управляемую и наблюдаемую часть;
2)управляемую, но ненаблюдаемую часть;
3)наблюдаемую, но неуправлямую часть;
4)неуправляемую и ненаблюдаемую часть.
139
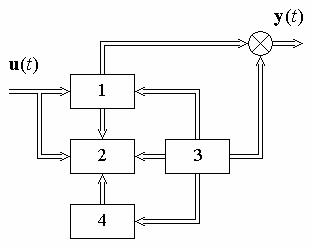
Рис. 6.7
Контрольные вопросы
1.Запишите дифференциальные уравнения «вход-выход» многомерных линейных объектов и систем.
2.Что такое передаточная матрица, как она определяется по дифференциальным уравнениям «вход-выход»?
3.Что такое весовая матрица, как она связана с передаточной матрицей?
4.Как определяется передаточная матрица замкнутой многомерной системы автоматического управления?
5.Что такое вектор состояния динамической системы, его размерность?
6.Запишите уравнения состояния и нарисуйте схему «вход- состояние-выход» динамической системы.
7.Формулировка критерия управляемости динамической системы.
8.Формулировка критерия наблюдаемости динамической системы.
9.Нарисуйте стуктурную схему полностью наблюдаемой, но неполностью управляемой системы системы.
10.Нарисуйте стуктурную схему полностью управляемой, но неполностью наблюдаемой системы.
11.Какие части с точки зрения управляемости и наблюдаемости может содержать динамическая система?
140
