
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
7.2 ] |
Интерференция монохроматических волн |
531 |
|
Чередование максимумов и минимумов интенсивности, ха- |
|
рактерное для интерференции, связано с изменением |
знака |
|
. |
|
|
В тех точках, где 2$ , интенсивность максимальна
и равна 2 1 2 2. Геометрическое место точек, удовлетворяющих этому условию, образует максимум (полосу) -го порядка. Там, где 2 1 $, возникают минимумы интенсивности (темные интерференционные полосы), для которых
2 |
1 |
2 |
. Контраст интерференционной картины приня- |
||||||
|
2 |
||||||||
то характеризовать величиной видности 2 , определяемой равен- |
|||||||||
ством |
|
|
2 |
+ + |
|
2 1 2 |
|
|
(7.5) |
|
|
|
|
||||||
|
|
|
|
+ + |
2 |
2 |
|
|
|
|
|
|
|
1 2 |
|
|
|||
Видность максимальна и равна единице при равных амплитудах 1 2 (при этом : 0). Видность близка к нулю, когда интенсивность одной из интерферирующих волн существенно больше другой.
Принцип суперпозиции справедлив, в силу линейности уравнения Гельмгольца, и для комплексных амплитуд (см. § 4.2): комплексная амплитуда результирующей волны 7 D
равна сумме комплексных амплитуд 71 1 D 1 и 72
2 D 2 слагаемых волн:
7 71 72
Соответственно, интенсивность результирующей волны
: 2 7 2 есть
|
: 71 72 |
2 |
|
|
|
|
|
|
|
||
Последнее равенство можно записать в виде |
|
|
|||
2 7 |
2 7 |
|
, |
(7.6) |
|
: 71 |
2 |
1 7 7 72 |
|||
|
|
2 |
1 |
|
|
где знак означает |
комплексно-сопряженную величину, |
:1 |
|||
71 2 и :2 72 2 — интенсивности слагаемых волн. Интерференционный эффект определяется двумя последними
слагаемыми в (7.6): 717 |
и 7 72 — это два комплексно-сопря- |
||||||||||||||
|
|
|
|
|
|
2 |
|
|
1 |
7 72 2 Re 7 72. |
|||||
женных слагаемых, поэтому 717 |
|||||||||||||||
Таким образом |
|
|
|
|
|
|
2 |
1 |
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
: 7 |
1 |
2 7 |
2 2 Re 7 7 |
2 |
|
(7.7) |
|||||||
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|||
Ясно, что интерференционное слагаемое в (7.3) имеет тот же |
|||||||||||||||
вид, что и в (7.7): |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 Re 7 7 |
2 |
2 Re |
1 |
D 1 |
2 |
D 2 |
2 Re |
|
D |
|
|||||
1 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|||
2 1 2

532 |
Интерференция волн |
[ Гл. 7 |
Большинство эффектов интерференции и дифракции, которые будут рассматриваться в данной и последующей главах, наилучшим образом иллюстрируются на примере видимого света, т. е. электромагнитных волн с 400–700 нм. При этом эффект интерференции проявляется в виде чередующихся светлых и темных полос на экране наблюдения.
Рассмотрим несколько характерных случаев интерференции монохроматических волн.
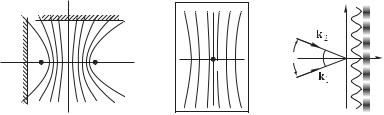
Интерференция сферических волн 1). Две сферические волны излучаются точечными источниками 91 и 92 (рис. 7.1). Комплексные амплитуды волн в точке наблюдения 6 есть
71 |
0 |
D 1 , |
72 |
0 |
D 2 |
|
|
||||
#1 |
|
#2 |
|
||
(мы полагаем, что источники излучают синфазно, с одинаковой амплитудой), 1 и 2 — расстояния от источников 91 и 91 до точки наблюдения.
Разность фаз |
колебаний |
в точке наблюдения , |
где 2 1 |
— разность |
хода волн, приходящих в точку |
наблюдения. При (разность хода равна целому числу длин волн) разность фаз 2$ и, следовательно, получаем интерференционный максимум -го порядка.
При 2 1 2 получаем интерференционный минимум.
Геометрическое место точек, для которых 2 1
— это гиперболоиды вращения. Таким образом поверхности интерференционных максимумов и минимумов — гиперболоиды, сечение которых плоскостью, в которой лежат источники 91 и 92 (плоскость рисунка) показаны на рис. 7.1.
Ясно, что форма полос, наблюдаемых на каком-либо плоском экране, зависит от положения этого экрана. Например, если плоскость наблюдения перпендикулярна линии 9192, соединяющей источники (плоскость П1 на рис. 7.1), то интерференционные полосы имеют вид чередующихся светлых и темных колец.
Если экран расположен параллельно линии 9192 (экран П2), то интерференционные полосы представляют собой семейство гипербол — почти параллельных прямых, если ограничиться
1) Нелишне напомнить, что поперечные электромагнитные волны в принципе не могут быть сферическими; их элементарный источник — не точка, а колеблющийся диполь. Тем не менее, в оптике нередко пользуются приближением сферической волны (точечного источника и точечного фокуса). Это означает, что интересующий нас участок волнового фронта имеет сферическую форму с точностью до малых поправок. Если же кривизна фронта существенна лишь в одной плоскости, а в ортогональной плоскости пренебрежимо мала, используется приближение цилиндрической волны.
7.2 ] |
Интерференция монохроматических волн |
533 |
достаточно малой областью вблизи центра экрана (точка на
рис. 7.2).
Целое число называется порядком интерференции. Нулевой порядок интерференции соответствует разности хода 0 (геометрическое место точек нулевой разности хода — плоскость симметрии на рис. 7.1).
|
O |
Ï2 |
|
|
x |
|
|
|
|
|
z |
Ï1 |
S1 |
|
O |
|
|
|
S2 |
|
|
||
|
O |
|
|
|
|
|
Рис. 7.1 |
Рис. 7.2 |
|
Рис. 7.3 |
|
Если рассматривать небольшую область наблюдения, в которой амплитуды колебаний двух слагаемых волн примерно одинаковы: 0 1 0 2 , то получаем
: 2:0 1 , |
(7.8) |
7 |
|
где — скорость волны, :0 — интенсивность каждой из волн в плоскости наблюдения.
Формула (7.8) имеет универсальный характер, она справедлива при интерференции любых монохроматических волн одинаковой частоты и интенсивности.
Интерференция плоских волн. Рассмотрим результат интерференции двух плоских волн, волновые векторы !1 и !2 которых составляют углы # с осью и лежат в плоскости рис. 7.3.
Проекции векторов !1 и !2 на ось равны нулю. Комплекс-
ные амплитуды волн есть соответственно, 7 |
1 |
|
D 1 1 , |
||||
|
|
|
|
1 |
|
|
|
72 2D 2 2 (см. § 1.2). Поскольку 1 |
#, 2 |
|
|||||
#, а -компоненты векторов 1 |
и 2 одинаковы и равны |
||||||
1 2 #, то имеем |
|
|
|
|
|
|
|
71 , 1D ' ' , 72 , |
2D |
' ' |
|||||
Результирующую картину интенсивности найдем, используя |
|||||||
общее соотношение (7.4): |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
(7.9) |
: 1 2 2 1 2 2 # |
|
||||||
Она не зависит от , т. е. одинакова в любой плоскости наблюдения и поскольку она не зависит от , то в любой
534 |
|
Интерференция волн |
|
|
|
|
[ Гл. 7 |
||||
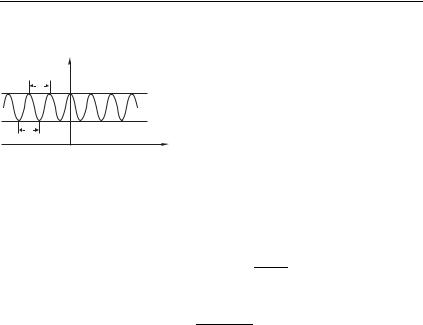
плоскости картина имеет вид чередующихся светлых |
|||||||||||
и темных полос, параллельных оси (т. е. перпендикулярных |
|||||||||||
|
I |
|
плоскости рисунка). Функция : |
||||||||
|
|
показана на рис. 7.4. |
|
|
|
||||||
|
|
|
|
|
|
||||||
|
l |
Imax |
|
Расстояние |
между |
двумя |
со- |
||||
|
седними максимумами интенсивно- |
||||||||||
|
|
|
|||||||||
|
|
Imin |
сти |
(интерференционными |
полоса- |
||||||
l |
|
|
ми) |
или |
между |
двумя |
соседни- |
||||
O |
x |
ми минимумами называют шириной |
|||||||||
|
|||||||||||
|
Рис. 7.4 |
|
интерференционной полосы |
(рас- |
|||||||
|
|
стояние на рис. 7.4). Переход от |
|||||||||
одной светлой полосы к другой соответствует изменению аргу- |
|||||||||||
мента косинуса в (7.9) на 2$ |
|
|
|
|
|
|
|
|
|||
2 # 2$,
откуда
|
|
|
|
|
|
2 |
|||
|
Обозначая через * угол схождения волн (* 2#), получаем
|
|
(7.10) |
2 '2 |
или для малых углов схождения: *2 *2
|
|
(7.11) |
|
' |
|
В оптике, в силу малости |
5 10 5 |
см), для получе- |
ния достаточно широких полос ( 0,1–1 см) угол схождения волн * приходится выбирать малым ( 10 4–10 5 радиан), поэтому практически всегда можно пользоваться приближенным выражением (7.11).
Для оценки минимально возможной ширины полосы необходимо, разумеется, использовать точное соотношение (7.10). Из него следует, что минимальная ширина интерференционных полос достигается при * $, т. е. при интерференции встречных
волн. Мы имеем при этом *2 1 и |
|
|
|
|
(7.12) |
|
2 |
|
Это, как мы знаем, есть расстояние между соседними пучностями (или узлами) в стоячей волне.
Из формулы (7.12) можно сделать достаточно общий вывод: в монохроматическом волновом поле характерный масштаб пространственных неоднородностей не может быть существенно меньшим длины волны .
7.3 ] |
Квазимонохроматические волны |
535 |
|
При интерференции плоских волн одинаковой |
амплитуды |
1 2 из (7.9) имеем |
|
|
|
: 2:0 1 2 # , |
(7.13) |
где :0 2 — интенсивности слагаемых волн. |
|
|
7.3. Квазимонохроматические волны
Элементарные представления о статистической природе излучения. В предыдущем параграфе мы говорили о волновых процессах, имеющих гармоническую зависимость от времени. Однако ни один реальный источник света не излучает волну, напряженность поля в которой меняется по гармоническому закону. Это подтверждается множеством экспериментальных фактов. Рассмотрим один из них: результат суперпозиции волн, излучаемых двумя независимыми источниками (например двумя электрическими лампочками).
Казалось бы, мы должны получить характерное чередование светлых и темных полос. Однако ничего подобного в действительности не происходит: если в комнате, где горит электрическая лампочка, зажечь еще одну точно такую же, то освещенность стен просто удваивается. Другими словами, при наложении света от двух лампочек складываются интенсивности и никаких интерференционных явлений не наблюдается.
Для того чтобы правильно ответить на возникающие вопросы и объяснить результат рассмотренного эксперимента (а также результаты множества других подобных фактов), необходимо отказаться от принятой ранее синусоидальной (гармонической) идеализации и более тщательно рассмотреть структуру оптического излучения.
Если бы мы имели столь малоинерционный прибор, что он мог бы следить за изменением напряженности электрического
поля в световой волне, испущенной каким-либо источником, то мы получили бы запись случайного процесса, а вовсе не
гармонический сигнал. Что мы понимаем |
|
|||
под словами случайный процесс? |
|
t |
||
Возьмем большое |
количество |
(ан- |
t |
|
самбль) одинаковых |
источников |
све- |
t |
|
та: одинаковых электрических лампочек |
||||
|
||||
или одинаковых кювет, наполненных на- |
t |
|||
гретым газом (одинаковые температура, |
||||
|
||||
давление, вообще все макроскопические |
Рис. 7.5 |
|||
параметры). |
|
|
||
|
|
|
||
Используя различные источники из ансамбля, мы будем полу- |
||||
чать различные записи колебательного процесса - (рис. 7.5).

536 Интерференция волн [ Гл. 7
Полученная совокупность записей представляет собой ансамбль случайных функций. Случайный характер процесса проявляется
в том, что каждый раз мы получаем новую функцию - , не
повторяющую в точности ни одну из других функций; при этом невозможно предсказать заранее, какую точно из реализаций ансамбля мы получим в данном эксперименте. Любую из записей - можно характеризовать лишь вероятностно
(определяя, например, вероятность, с которой то или иное
значение принимает функция в любой момент времени). В этом состоит отличие случайного процесса, определяемого вероятностными законами, от процесса детерминированного,
в котором каждое значение измеряемой величины абсолютно точно предсказуемо.
Статистический характер светового излучения обусловлен фундаментальными физическими свойствами источника. Всякий реальный источник — это совокупность огромного числа атомов. Каждый из атомов может стать элементарным источником излучения, если благодаря какому-либо механизму (столкновение с другим атомом, электронный удар и т. д.) он будет переведен в возбужденное состояние. Случайный, статистический харак-
тер механизма возбуждения определяет статистическую природу излучения. Любой из атомов может начать высвечиваться в произвольный, случайный момент времени . Другое важное
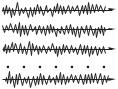
обстоятельство связано с характером излучения отдельного атома. Возбужденный атом излучает конечное время. С классиче-
ской точки зрения атом можно рассматривать как колебательную |
|||||||||
|
ei |
|
систему (осциллятор) с определенной доброт- |
||||||
|
|
ностью. Излучение такого осциллятора пред- |
|||||||
|
|
||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
ставляет собой процесс свободных затухаю- |
|
|
|
|
|
|
|
|
|
|
щих колебаний. Мы приходим, таким обра- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зом, к картине, изображенной на рис. 7.6 (под |
|
ti |
t |
|||||||
|
D можно понимать изменение напряженно- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сти электрического поля в цуге излучения). |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.6 |
|
Нужно отметить, что атомные системы обла- |
||||
|
|
|
|
|
|
|
|
|
дают чрезвычайно малым затуханием (высо- |
кой добротностью), поэтому длительность цуга >0 существенно больше периода колебания: >0 (характерные длительности цугов для оптического диапазона излучения >0 10 8–10 10 с, что на много порядков превышает период светового колебания10 15 с). Возбужденный атом, излучая цуг, постепенно теряет энергию и по прошествии времени порядка >0 переходит
в основное, невозбужденное состояние; говорят, что длительность цуга есть время жизни атома в возбужденном состоя-
нии. Последовательность цугов, излучаемых атомом какого-либо источника света, показана на рис. 7.7. Статистический характер

7.3 ] Квазимонохроматические волны 537
механизма возбуждения приводит к тому, что моменты возникновения излучаемых цугов 1, 2, , являются случайными независимыми величинами.
Наконец, важно иметь в ви- |
|
|
|
||
ду, |
что в |
излучении одновре- t1 |
t2 |
t3 |
t |
менно принимает участие боль- |
|
|
|
||
шое |
число |
атомов. Обозначая |
|
Рис. 7.7 |
|
последовательность цугов, излучаемых каким-либо -м атомом через D , запишем суммарное излучение в виде
- D , |
(7.14) |
|
|
причем сумма (7.14) содержит в каждый момент времени огромное число «живых» (отличных от нуля) слагаемых.
Попробуем качественно описать свойства суммарного колебания (7.14), исходя из представления о цугах конечной продолжительности >0 и случайном характере их возникновения. Ясно, что вклад в суммарное колебание в некоторый момент времени вносят лишь те цуги, начало которых лежит в интервале от >0 до , поскольку все цуги, начавшиеся до момента >0, успевают затухнуть к моменту . Для уяснения качественной картины будем полагать, что число «живых» слагаемых в сумме (7.14)
(т. е. число излучающих в каждый момент времени атомов) равно !. Поскольку любой атом с равной вероятностью может
начать излучать в любой момент времени , то среднее число цугов, начало которых приходится на любой малый интервал
времени равно ! >0.
Таким образом, доля цугов, заканчивающихся за время и заменяющихся новыми, равна >0, причем через время >0 в сумме (7.14) все ! излучающих цугов заменяются новым набором.
Все сказанное выше можно пояснить, используя векторную диаграмму. Вектор, изображающий суммарное колебание (7.14), представляется на векторной диаграмме суммой большого числа
|
|
|
|
элементарных векторов, соответствующих из- |
|
|
) |
|
лучению отдельных атомов (рис. 7.8). Ориен- |
|
t |
|
|
|
( |
|
|
тация каждого элементарного вектора на этой |
|
a |
|
|
|
|
|
|
(t) |
x диаграмме случайна. За время, малое по срав- |
|
|
|
|
|
нению с длительностью цуга >0, ориентация |
|
|
|
|
|
|
|
|
|
суммарного вектора и его длина изменятся |
|
|
|
|
несущественно, так как лишь небольшая часть |
|
|
Рис. 7.8 |
|
элементарных векторов заменится другими. Че- |
|
|
|
|
рез время порядка >0 возникает совершенно |
новая совокупность элементарных векторов, что приводит к новым значениям длины и угла наклона суммарного вектора, которые не связаны со старыми значениями этих величин.
538 |
Интерференция волн |
[ Гл. 7 |
Причем качественно ясно, что случайные функции и могут изменяться независимо друг от друга. Действительно, при
другой реализации направлений элементарных векторов может образоваться суммарный вектор той же длины , но имеющий произвольное направление : угол наклона суммарного векто-
ра никак не связан с его длиной. Можно сказать, что случайные функции и статистически независимы.
Как следует из изложенного выше, амплитуда и фаза суммарного колебания испытывают случайные изменения с харак-
терным временным масштабом >0. Мы приходим, таким образом, к представлению о квазимонохроматическом процессе и можем
записать колебание (7.14) в виде
- 0 , |
(7.15) |
где и — медленно и хаотически меняющиеся функции.
Характерный временной масштаб их изменения >0 носит название времени корреляции или времени когерентности. Принято говорить, что значения и > коррелированы при > ' >0 и некоррелированы при > & >0. Это же относится и к значениям
фазы и > . Еще раз напомним: мы полагаем, что функции и остаются практически неизменными на интервалах времени , содержащих большое число периодов светового колебания 2$ 0. Именно в этом смысле понимается медленность их изменения и именно поэтому процесс (7.15) является квазимонохроматическим.
Итак, квазимонохроматическое колебание (7.15) изображается на векторной диаграмме в виде вектора с медленно и хаоти-
чески изменяющимися длиной и направлением. Этому вектору соответствует комплексная функция
7 D , |
(7.16) |
которая является аналогом комплексной амплитуды гармонического процесса и которую можно назвать комплексной амплитудой квазимонохроматического процесса (7.15). Мы будем пользоваться комплексным представлением квазимонохроматических колебаний, ставя в соответствие реальному процессу (7.15) комплексную функцию
2 D # 7 D # |
(7.17) |
Подчеркнем, что в выражении (7.17) статистический (случайный) характер имеет первый сомножитель — комплексная амплитуда 7 , второй же сомножитель D # описывает гармоническое колебание с частотой .
Можно сказать, что 7 является медленно и хаотически меняющейся огибающей в случайном процессе 2 , т. е. функция

7.3 ] Квазимонохроматические волны 539
7 описывает закон случайной амплитудно-фазовой модуляции гармонического процесса. Реальное возмущение - связано с 2 формулой
- Re 2 Re 7 D # |
(7.18) |
Поскольку в дальнейшем мы будем использовать комплексное представление (7.17), необходимо установить соотношение между комплексной функцией 2 и результатами экспериментальных наблюдений.
Сделаем несколько замечаний о свойствах фотоприемника, с помощью которого проводится анализ светового излучения.
Таким фотоприемником может быть глаз, фотопластинка, фотоэлемент и т. д. Все эти устройства регистрируют поток энергии,
усредненный за некоторое, характерное для данного фотоприемника, время , которое можно назвать временем регистрации (или постоянной времени фотоприемника). Посколь-
ку световой поток (поток энергии) пропорционален квадрату напряженности поля -2 в волне, то регистрируется величина
|
1 |
1 2 |
|
|
: |
-2 , |
(7.19) |
||
|
||||
|
|
1 2 |
|
называемая интенсивностью света.
Постоянные времени разных приемников сильно различаются: у сетчатки глаза время регистрации 10 1 с (глаз не успевает замечать мелькания кадров на экране кино и телевизора). Время экспозиции фотоматериалов обычно10 2–10 4 с, хотя может быть и минуты, и даже часы. У некоторых типов фотоэлементов время регистрации 10 6– 10 8 с. Результат измерения существенно зависит от соотношения между временем экспозиции и характерным временным масштабом регистрируемых процессов.
Квазимонохроматические колебания характеризуются двумя временными масштабами: периодом «несущего колебания»0 2$ 0 и временем когерентности >0. В диапазоне видимого света, как отмечалось выше, 0 10 15 с, а время когерентности даже для самых узких спектральных линий не превышает значений >0 10 7–10 8 с (излучение когерентных источников света — лазеров — имеет время когерентности на несколько порядков больше). Таким образом, в оптике всегда 0 — не существует фоторегистрирующих устройств, способных следить за отдельным периодом светового колебания. Однако при сравнении и >0 можно выделить два случая:

540 |
Интерференция волн |
[ Гл. 7 |
1.>0. Такой фотоприемник может следить за случайными изменениями светового потока, обусловленными конечной длительностью цугов излучения атомов.
2.>0. Фотоприемник регистрирует средний световой поток (среднюю интенсивность). Этот способ регистрации можно назвать инерционным. Именно этот случай реализуется в большинстве оптических экспериментов и именно его мы будем иметь
ввиду в дальнейшем.
Используя (7.15), перепишем (7.19) в виде
|
|
|
|
1 |
1 2 |
|
|
|
|
|
|||
|
|
: |
|
|
2 2 |
|
|||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
1 2 |
|
|
|
|
|
||
Выражая квадрат косинуса с помощью равенства 2 # |
|||||||||||||
1 2 1 2# , получим |
|
|
|
|
|||||||||
1 |
1 2 |
|
|
|
|
|
|
1 |
1 2 |
|
|
|
|
|
2 |
|
|
2 |
|
2 0 |
2 |
||||||
: |
|
|
|
|
|
|
|||||||
2 |
|
|
|
2 |
|
||||||||
|
|
1 2 |
|
|
|
|
|
|
|
1 2 |
|
|
|
(7.20) За время наблюдения подынтегральная функция во втором слагаемом в формуле (7.20), осциллируя с удвоенной световой частотой, многократно меняет знак, поэтому второй интеграл
пренебрежимо мал в сравнении с первым, тогда
|
1 |
|
1 |
1 2 |
|
|
||
|
|
|
|
2 |
||||
: |
2 |
|
||||||
2 |
|
|
|
2 |
|
|||
1 2
(черта означает усреднение по времени регистрации). С другой стороны, используя (7.16), имеем
7 7 D D 2
Таким образом, наблюдаемая интенсивность выражается через комплексную амплитуду 7 равенством
: 12 7 7
Очевидно теперь, что интенсивность можно выразить аналогичным образом и через комплексную функцию 2 (исполь-
зуя (7.17)):
: 12 2 2
