
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
6.5 ] Излучение колеблющегося диполя 521
в направлении своей оси колеблющийся диполь не излучает!
Найдем общую мощность, излучаемую диполем по всем направлениям. Рассмотрим на волновой поверхности — сфере радиуса — элементарное колечко, заштрихованное на рис. 6.11 б. Его площадь
2$ B 2$ 2 B |
(6.27) |
||
Средний поток энергии через это кольцо |
|
|
, а пол- |
9 |
|||
ная энергия, излучаемая в 1 с по всем направлениям 6 9 . Используя (6.26), находим
2
|
|
4&2 |
|
3 B |
|
4&2 |
(6.28) |
6 |
0 |
0 |
|||||
1600273 |
|
120073 |
|||||
2
Важное следствие полученного выражения: энергия, излучаемая диполем за 1 с, быстро (пропорционально 4) растет с ростом частоты и именно поэтому для передачи радиосигналов используются высокие частоты (в радиовещании от 105 до 108 Гц, что соответствует длинам волн от 3 км до 3 м).
Поскольку колеблющийся диполь излучает энергию, то для поддержания незатухающих гармонических колебаний необходим источник, восполняющий потерю энергии, равную 6. Выражение (6.28) можно представить в виде, аналогичном формуле 6 :2 2, определяющей мощность джоулевых потерь в колебательном контуре с сопротивлением . Поскольку заряд колеблющегося диполя меняется по закону / /0 , то ток
: / /0 :0 , где :0 /0 80 . Исполь- зуя последнее выражение, получим из (6.28):
6 |
2 2 |
2 |
(6.29) |
|
12007 |
3 |
:0 |
||
|
|
|
|
|
Роль сопротивления играет величина
2 2
изл 60073
При таком определении формула (6.29) принимает вид
2
6 изл2 +0
Введенная величина изл играет для потерь на излучение ту
же роль, что и сопротивление контура для потерь на нагревание. Величина изл называется сопротивлением излучения.
Вернемся к классической модели атома, согласно которой электрон в атоме совершает гармонические колебания (как ко-
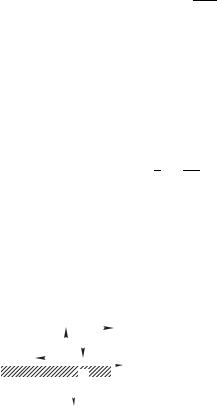
522 |
Электромагнитные волны |
[ Гл. 6 |
леблющийся осциллятор): 0 . Энергия, запасенная ос-
циллирующим электроном, равна ) 2 2 2 2. Вычисляя ее в момент, когда электрон проходит положение равновесия
( 0 и 0), найдем ) 2 02 2 2820 2/2 . Потери энергии за период колебаний, связанные с излучением, равны
) 6 6 2$ , где 6 определяется формулой (6.29). Добротность нашей колебательной системы найдем, используя (2.42):
C 2$ |
> |
|
3 73 |
|
|
|
|||
|
2 52 |
|||
|
> |
|||
Для электрона, колеблющегося с частотой 2$ 6 1014 Гц (излучение зеленого света), используя числовые значения9,1 10 31 кг, / 1,6 10 19 Кл, получим
C 1,4 107
Столь высокой добротностью не обладает ни одна «рукотворная» колебательная система. Время затухания (в течение которого амплитуда осцилляций уменьшается в D раз) равно
> Æ1 29 7,7 10 9 с
Затухание осциллятора, обусловленное излучением электромагнитной волны, называют радиационным затуханием.
6.6. Отражение электромагнитной волны от идеального проводника
Напомним основные результаты решения задачи, рассмот- |
|||||||||||
ренной ранее в § 2.5. Пусть плоская электромагнитная волна, |
|||||||||||
|
|
|
|
|
|
|
бегущая вдоль оси , падает на плоскую |
||||
|
k |
|
|
E1 |
|
поверхность идеального проводника (по- |
|||||
1 |
|
|
|
||||||||
E |
|
|
k1 |
|
верхность |
|
0, рис. 6.12) |
||||
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
-1 -1 , , |
||||
|
|
|
O |
|
|||||||
Идеальный |
|
|
|
(6.30) |
|||||||
|
|
|
|
|
|
||||||
проводник |
|
z |
|
1 1 , |
|
|
|
||||
|
|
0! |
|||||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||
Рис. 6.12 |
|
|
|
7 |
|
||||||
|
|
|
|
|
|
||||||
Волна (6.30) линейно-поляризована: вектор имеет только -компоненту, а вектор только-компоненту (ось перпендикулярна плоскости рисунка и направлена к читателю).
Как известно, на поверхности проводника (при 0) должно выполняться граничное условие
- 0, 0 |
(6.31) |

6.6 ] |
Отражение электромагнитной волны |
523 |
(равенство нулю тангенциальной компоненты электрического поля). Это условие окажется выполненным, если мы предположим, что наряду с падающей на поверхность проводника волной (6.30) возникает отраженная волна
-1 , ,
(6.32)
1 , 0!
7
Направление отраженной волны противоположно положительному направлению оси , поэтому аргумент косинуса в (6.32) есть . Кроме того, векторы , и ! должны составлять «правую» тройку (как в любой бегущей плоской электромагнитной волне), поэтому при изменении направления волны на противоположное изменяется и направление одного из векторов — либо , либо . Граничное условие (6.31) принимает вид
- 0, - |
1 |
0, - |
|
0, 0 |
(6.33) |
|
1 |
|
|
Подставляя (6.30) и (6.32) в граничное условие (6.33), получаем , т. е. амплитуда отраженной волны равна амплитуде падающей волны — коэффициент отражения равен единице, а знак « » в последнем равенстве означает, что на поверхности проводника (при 0) колебания поля -1 в отраженной волне происходят в противофазе с колебаниями поля -1 в падающей
волне:
-1 , ,
(6.34)
1 , 0!
7
Тогда результирующая волна в диэлектрике (расположенном над проводником), т. е. сумма волн (6.34) и (6.30), есть
- , -1 , -1 , 2 ,
(6.35)
, 1 , 1 , 2 0!
7
Последние формулы описывают стоячую электромагнитную волну, в которой на поверхности проводника (при 0) находится узел электрического поля - 0, 0 и пучность магнитного поля 0, 2 <1 .
Заметим, что разрыв тангенциальных компонент магнитного поля (внутри идеального проводника 0) обусловлен токами проводимости, которые индуцируются падающей электромагнитной волной.

524 |
|
|
|
|
Электромагнитные волны |
|
[ Гл. 6 |
|
|
|
|
|
|
6.7. Волноводы |
|
|
|
|
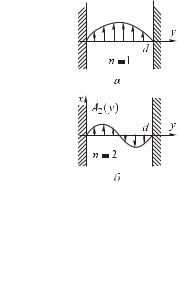
Пусть плоская электромагнитная волна падает на поверх- |
|||||||
ность идеального проводника, как показано на рис. 6.13: век- |
||||||||
тор k лежит в плоскости — на этот раз мы выбрали оси |
||||||||
|
|
|
|
|
координат так, что плоскость совпа- |
|||
|
|
|
|
k |
дает с плоскостью |
рисунка, |
причем ось |
|
E1 |
k |
|
E |
1 |
перпендикулярна |
плоской |
поверхности |
|
1 |
|
|||||||
|
1 |
|
||||||
|
|
|
+ |
|
z проводника, а ось параллельна поверх- |
|||
|
|
|
O |
|
ности т. е. плоская поверхность проводни- |
|||
|
|
|
y |
|
ка — плоскость . |
|
|
|
|
|
|
|
Будем полагать, что падающая волна |
||||
|
|
|
|
|
||||
|
Рис. 6.13 |
|
линейно-поляризована, причем вектор |
E |
||||
|
|
перпендикулярен плоскости |
рисунка |
, |
||||
|
|
|
|
|
||||
т. е. имеет только -компоненту и, следовательно, параллелен |
||||||||
поверхности проводника. Уравнение падающей волны имеет вид |
||||||||
-1 , |
(6.36) |
-компонента вектора ! равна нулю, # и # — соответственно - и -компоненты вектора !1, # — угол между вектором !1 и осью .
Вновь полагаем, что наряду с волной -1 возникает отражен-
ная волна
-1 ,
причем ее амплитуда 1, направление распространения # и начальная фаза должны быть выбраны так, чтобы выполнялось граничное условие — равенство нулю тангенциальной компоненты вектора в суммарной волне на поверхности (при 0). Легко видеть, что это условие выполняется, если амплитуда отраженной волны равна амплитуде падающей волны ( ), угол
падения равен углу отражения (# # ), а колебания - |
|
на по- |
||
|
|
1 |
|
|
верхности (при 0) противофазны с колебаниями -1 |
$ , |
|||
т. е. |
|
-1 $ , |
|
(6.37) |
|
|
|
||
вектор |
|
! отраженной волны имеет компоненты |
|
, |
|
|
|
|
|
|
|
поэтому аргумент косинуса содержит слагаемое |
||
|
|
|
|
|
вместо слагаемого в падающей волне. |
|
|
||
Действительно, суммарная волна над проводящей стенкой |
||||
(сумма волн (6.36) и (6.37)) имеет вид |
|
|
||
|
|
- , , 2 |
|
(6.38) |
На проводящей поверхности (при 0)
-0, , 0,
т.е. требуемое граничное условие выполняется.
6.7 ] |
Волноводы |
525 |
|
Обратим теперь внимание, что если на расстоянии |
от про- |
водящий стенки (т. е. при ) установить вторую проводящую стенку (параллельно первой), причем выбрать расстояние между
стенками так, чтобы $ , т. е. |
|
|
|
1, 2, 3 , |
(6.39) |
|
|
|
то волна (6.38) в области между стенками 0 ' ' |
не изме- |
|
нится, поскольку необходимые граничные условия — равенство нулю тангенциальной компоненты поля на проводящих поверхностях (при 0 и ), автоматически выполняются. При условии (6.39) имеем из (6.38)
- , , 2 $ , |
(6.40) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
||||
|
|
2 |
|
|
|
|
|
2 |
|
(6.41) |
|
|
|
|
7 |
|
|
|
|
|
|||
Итак, между двумя параллельными проводящими стенками, расположенными на расстоянии друг от друга (коридор между стенками представляет собой простейший волновод) могут распространяться волны вида (6.40): каждому значению отвечает свой тип волны — своя «мода» волновода, разным модам отвечают различные конфигурации поля — различные распределения амплитуды колебаний в фиксированном сечении 
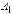
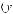
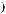
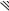
2 $ |
(6.42) |
|
||
|
|
|
O |
|
На рис. 6.14 показаны распределения ам- |
||||
|
||||
плитуды , отвечающие индексам 1 |
|
|||
и 2. Как и должно быть в соответ- |
|
|||
ствии с граничными условиями, 0 |
|
|||
при 0 и |
(ось волновода — ось — |
|
||
перпендикулярна плоскости рис. 6.14, а вектор |
O |
|||
в волне параллелен оси ). |
|
|||
Каждый тип волны, отвечающий фикси- |
|
|||
рованному значению , можно рассматривать |
|
|||
как суперпозицию плоской волны, падающей |
Рис. 6.14 |
|||
на проводящую стенку, и волны, отраженной |
||||
|
||||
стенкой, т. е. каждый тип волны образован суммой двух плоских |
||||
волн, волновые векторы которых k и |
! составляют угол # |
|||
с осью волновода, причем разным отвечают различные углы #: |
||||
# |
0 |
, |
(6.43) |
|||
|
|
|
||||
|
2 |
|||||
|
|
|
||||
где 0 2$ 2$ — длина волны в вакууме.

526 |
Электромагнитные волны |
[ Гл. 6 |
Поверхности |
одинаковой фазы колебаний, как видно |
|
из (6.40) — это |
поверхности . Это |
утверждение |
вданном случае означает, что в плоскости колебания либо синфазны как, например, в моде 1, либо отличаются по фазе на $ как, например, в моде 2, где колебания в области 0 ' ' 2 сдвинуты по фазе на $ по отношению к колебаниям
вобласти 2 ' ' .
Волновые поверхности перемещаются вдоль оси волновода — оси , причем фазовая скорость может быть найдена из (6.40)
и (6.41)
,
откуда |
|
|
|
|
|
|||
ф |
|
|
|
|
|
|
7 |
(6.44) |
|
|
|
1 2 0 2 2 |
|||||
|
7 2 2 2 |
|||||||
|
|
|
|
|
||||
Как ясно из (6.44), фазовая скорость волн в волноводе больше скорости света в вакууме.
Расстояние между волновыми поверхностями, на которых фаза колебаний отличается на 2$ (т. е. колебания синфазны) — это длина волны в волноводе, равная
|
2 |
0 |
& |
|
(6.45) |
||
|
|
|
|
|
|||
|
|
|
|||||
|
|
||||||
1 2 0 2 2 0 |
|
|
|||||
Итак, длина волны в волноводе больше длины волны той же частоты в вакууме.
Наконец, из (6.40) ясно, что если — действительное число, то - , , действительно представляет собой бегущую вдоль оси волну с перемещающимися волновыми поверхностями. Из (6.41) следует, что для этого необходимо выполнение нера-
венства |
2 |
2 2 |
|
|
7 |
|
|
Таким образом, существует критическая частота кр — минимальная частота волны, которая может распространяться
(бежать) по волноводу. Эта частота отвечает значению 1
кр 7 |
|
(6.46) |
|
|
|
Соответствующая длина волны в вакууме кр 2$ кр2 — это максимальное значение длины волны в вакууме, которая может бежать по волноводу. Критическому условию отвечает угол # (направление пары плоских волн, составляющих моду волновода), равный, согласно (6.43):
# |
кр |
1, |
т. е. # |
|
|||
2 |
|
2 |
|
6.8 ] |
Электромагнитная волна на границе раздела диэлектриков |
527 |
||||
|
Такая пара волн образует, как мы знаем, стоячую волну |
|||||
между стенками, которая никуда не распространяется. Узлы |
||||||
стоячей волны должны находиться на проводящих стенках (что- |
||||||
бы выполнялись требуемые граничные условия). Ясно, что при |
||||||
0 & кр 2 половина длины волны (расстояние между узла- |
||||||
ми) «не умещается» между стенками, и поэтому для таких волн |
||||||
необходимые граничные условия не могут быть выполнены. |
||||||
|
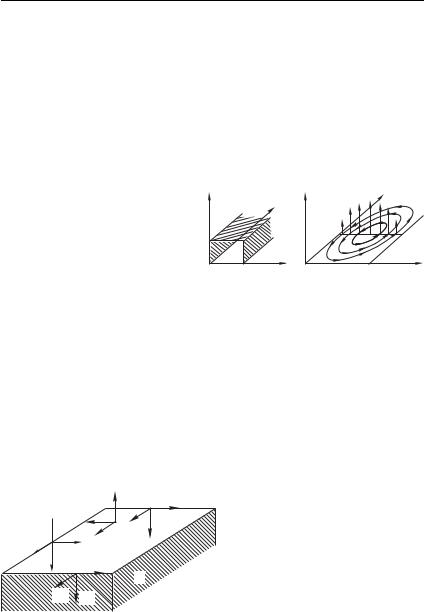
Разумеется, мы описали здесь лишь простейшие типы волн |
|||||
в волноводе с проводящими параллельными |
стенками, |
типы, |
||||
в которых поле E параллельно стенкам (оси ) и перпенди- |
||||||
кулярно оси волновода — оси |
(рис. |
6.15 а). В таких |
типах |
|||
волн магнитное поле B име- |
|
|
|
|
z |
|
ет проекцию на ось — на- |
|
x |
z |
x |
||
|
B |
|||||
правление распространения, |
|
|
E |
|||
|
|
|
|
|
||
т. е. электромагнитная вол- |
|
|
|
|
|
|
на в волноводе не является |
|
|
y |
|
y |
|
поперечной (в данном слу- |
|
d |
d |
|||
|
|
|
||||
чае поперечно поле E, и не |
O |
à |
O |
á |
|
|
поперечно поле B). Рису- |
|
|
Рис. 6.15 |
|
||
нок 6.15 б иллюстрирует это |
|
|
|
|||
|
|
|
|
|
||
обстоятельство: линии магнитного поля B (перпендикулярного |
||||||
оси , т. е. полю ) «охватывают» линии поля . |
|
|||||
6.8. Электромагнитная волна на границе раздела двух диэлектриков
Полностью задача падения электромагнитной волны на границу раздела двух диэлектриков решена в § 11.3. Здесь мы приведем лишь результаты, относящиеся к нормальному падению (рис. 6.16), чтобы обратить внимание на аналогию с поведением
|
|
|
|
|
звуковых волн на |
границе |
|
|
|
k |
|
|
раздела двух сред с различ- |
||
|
1 |
1 |
|
|
ными акустическими свой- |
||
|
E |
|
|
E1 |
|
|
|
|
|
H1 k |
|
ствами. |
|
|
|
|
|
H |
1 |
|
Для того |
чтобы |
необхо- |
|
x |
|
|
||||
|
1 |
|
|
димые граничные условия: |
|||
y |
|
1 |
|
|
|||
z |
|
E2 |
|
|
- 1 - 2, |
|
|
|
|
2 |
|
|
G 1 G 2 |
||
H2 |
k |
2 |
|
|
|
|
(6.47) |
|
|
|
|
— непрерывность тангенци- |
|||
|
|
|
|
|
|||
|
Рис. 6.16 |
|
|
альных компонент |
векторов |
||
|
|
|
E и H на границе |
раздела |
|||
|
|
|
|
|
|||
двух диэлектриков — оказались выполненными, вновь предположим, что в диэлектрике 1 с диэлектрической проницаемостью <1 (расположенном над границей раздела 0 на рис 6.16) наряду

528 Электромагнитные волны [ Гл. 6
с падающей волной
-1 , 1 1 , G1 , < 1 1 1
(6.48)
возникает отраженная волна
-1 , 1 1 , G1 , < 1 1 1 , (6.49)
а в диэлектрике 2 (<2), расположенном под границей 0 — прошедшая волна:
|
-2 , -2 |
2 2 , |
|
|
(6.50) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G2 , G2 < 1 2 2 |
|
|||||||||||
|
|
|
|||||||||||
|
Для волн ( 1, 1) и ( |
, ) в диэлектрике 1 |
1 1 |
||||||||||
|
|
|
|
1 |
|
1 |
|
|
|
|
2 2 2 |
||
1; для волны ( 2, 2) в диэлектрике |
|||||||||||||
2, где величины 1 |
|
и 2 |
|
называются |
|||||||||
<111 |
<212 |
||||||||||||
показателями преломления. Граничные условия (6.47) можно |
|||||||||||||
теперь записать в виде |
|
|
|
|
|
|
|
|
|
|
|
||
- |
0, - |
0, - |
0, , |
|
|
G |
0, G |
0, G |
0, |
||||
1 |
1 |
2 |
|
|
|
1 |
1 |
|
2 |
|
|||
Используя выражения (6.48), (6.49) и (6.50) при 0, после несложных вычислений получим формулы, связывающие амплитуды отраженной и прошедшей волны с амплитудой падающей
волны |
1 |
2 |
, |
|
|
|
2 1 |
|
(6.51) |
|
|
|
|
|
|
||||||
|
|
|
1 |
2 |
|
1 |
||||
|
|
|||||||||
1 |
1 |
2 |
|
|
|
1 2 |
|
|
||
|
|
|
|
|
|
|
||||
(При 1 ' 2 1 и 2 имеют разные знаки. Это означает, что в отраженной волне колебания вектора 1 противофазны колебаниям вектора 1 в падающей волне при 0. При этом колебания магнитных полей, как видно из (6.49), оказываются синфазными. Рисунок 6.16 соответствует именно этому случаю.)
Для коэффициентов отражения и прохождения, равных соответственно отношению средних за период потоков энергии
вотраженной и прошедшей волнах к среднему потоку энергии
впадающей волне, находим
1 2 |
2 |
|
4 1 2 |
|
|
||
, |
|
|
(6.52) |
||||
|
|
|
|
2 |
|||
|
1 2 |
1 2 |
|||||
|
|
|
|
||||
|
|
|
|
|
|||
Обратите внимание на замечательное сходство полученных выражений с формулами (5.40), определяющими коэффициенты отражения и прохождения звуковой волны, падающей на границу раздела двух сред с различными значениями -3 (- — модуль упругости, 3 — плотность).
Эта величина для акустических волн играет ту же роль, что и показатель преломления <1 для электромагнитной волны.
Г л а в а 7
ИНТЕРФЕРЕНЦИЯ ВОЛН
7.1. Принцип суперпозиции волн
Пусть в некоторой среде один источник создает волновой процесс 1 , , а другой — волновой процесс 2 , . Согласно принципу суперпозиции, если излучают одновременно два источника, то результирующий волновой процесс , есть
, 1 , 2 , |
(7.1) |
Смысл этого равенства состоит в том, что распространяющиеся одновременно волны не влияют друг на друга, поэтому результирующее возмущение есть просто сумма неискажающих друг друга возмущений. Другими словами, в равенстве (7.1)1 , — это волна, которую создавал бы первый источник (если бы второй волны не было), так же как 2 , — это волна, которую создавал бы второй источник в отсутствие первого.
Опыт подтверждает справедливость принципа суперпозиции в широких пределах: свету далекой звезды, идущему к нам из космоса, не мешает распространяться свет других звезд или свет горящей поблизости лампочки; радиоволны, заполняющие все окружающее пространство, не влияют друг на друга — вращая ручку настройки приемника, мы ловим передачу определенной радиостанции, несмотря на то, что приемник буквально погружен в океан радиоволн; звуки голосов многих людей, разговаривающих в комнате, не отскакивают друг от друга, подобно бильярдным шарам — они беспрепятственно проходят друг сквозь друга, не искажая друг друга.
Итак, для всех линейных волн независимо от их природы, справедлив принцип суперпозиции: можно сказать, что линейность волнового уравнения является математическим отражением (следствием) принципа суперпозиции: если возможны решения 1 , и 2 , , то возможно также и решение (7.1).
Рассматривая в двух последующих главах явления интерференции и дифракции, мы будем иметь в виду либо скалярные, либо векторные, но одинаково поляризованные волны. Под - понимается, таким образом, либо колебания плотности среды при распространении в ней звуковой волны, либо колебания проекции электрического поля в электромагнитной волне (полагаем при этом, что все волны имеют, скажем, только -компоненту),

530 |
Интерференция волн |
[ Гл. 7 |
либо какую-либо другую величину, изменяющуюся по волновым законам. При этом векторная сумма (7.1) заменяется скалярной суммой
- , -1 , -2 , |
(7.2) |
Каков же результат наложения двух волн? Рассмотрим вначале наиболее простой, и в то же время исключительно важный случай, а именно, монохроматические волны.
7.2. Интерференция монохроматических волн
Итак, пусть в пространстве распространяются две монохроматические волны одинаковой частоты :
-1 , 1 1 , -2 , |
2 2 |
Согласно принципу суперпозиции |
колебательный процесс |
в любой точке наблюдения (радиус-вектор фиксирован) есть сумма гармонических колебаний. Квадрат амплитуды (т. е. интенсивность) результирующего колебания найдем, используя (1.7) (см. § 1.2):
|
2 2 |
2 |
|
2 1 2 , |
(7.3) |
1 |
2 |
|
где 2 1 — разность фаз слагаемых колебаний в точке наблюдения. Напомним, что интенсивность : 2 — это величина, равная (с точностью до константы) плотности потока
энергии в монохроматической волне. Равенство (7.3) показывает, что плотность потока энергии в результирующей волне не равна в общем случае сумме плотностей потоков энергии в слагаемых волнах. В пространстве, где налагаются два волновых процесса, происходит перераспределение потоков энер-
гий: в некоторых точках пространства результирующая интен-
сивность оказывается больше суммы интенсивностей :1 21 и
:2 22 слагаемых волн; в других точках, наоборот, результиру-
ющая интенсивность меньше суммы интенсивностей. Результат зависит от интерференционного слагаемого 2 1 2 ,
т. е. от разности фаз колебаний в данной точке наблюдения.
Явление наложения волн, при котором результирующая ин-
тенсивность оказывается не равной в общем случае сумме интенсивностей слагаемых волн, называется интерференцией.
Соотношение (7.3) является основным для описания интерференции двух монохроматических волн. Оно может быть записано в виде
: :1 :2 2 :1:2 |
(7.4) |
