
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
6.1 ] Уравнения Максвелла и волновое уравнение 511
пар, например - и . Продифференцируем первое из уравнений (6.8) по , а второе — по . Мы получим
|
2* |
|
2 |
, |
|
2 |
|
0! 2* |
|
|
||||
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
72 2 |
|
|||||||||
|
|
|
||||||||||||
Исключая смешанную производную .2 . . .2 . . |
||||||||||||||
из этой пары уравнений, получаем |
|
|
|
|
|
|
||||||||
|
|
|
2* |
0! 2* |
|
|
|
|
|
(6.10) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
72 2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
Мы пришли к важному результату: поле - , подчиняется волновому уравнению, т. е. изменение во времени и пространстве электрического поля - происходит по законам распространения волн, в частности, описывается функцией вида
- , -
Эта функция, как мы знаем, описывает волну, распространяющуюся вдоль оси (в положительном (знак « »), либо в отрицательном (знак « ») направлении оси ), причем скорость волны , как следует из (6.10), есть
|
|
7 |
|
(6.11) |
|
|
0! |
|
|
Константа |
определяет скорость электромагнитной |
волны |
||
в вакууме (< 1 1) и равна
2,998 108 м/с 3 108 м/с
Это одна из самых замечательных мировых констант в физике. Мы могли бы, дифференцируя первое из уравнений (6.8) по , а второе — по , получить (исключив из системы смешанную
производную .2- . . .2- . .) волновое уравнение для магнитного поля :
2 0! 2 ,2 72 2
т. е. точно такое же волновое уравнение, что и (6.10). Этому уравнению подчиняется волновой процесс вида
,
Волна бежит вдоль оси с той же скоростью, что и волна
- . Эта пара волн - , представляет собой бегущую вдоль оси плоскую электромагнитную волну, в которой поле име-
ет только -компоненту, а поле имеет только -компоненту, т. е. колебания полей и происходят в плоскости, перпендикулярной направлению распространения — оси . Итак, плоская

512 |
Электромагнитные волны |
[ Гл. 6 |
электромагнитная волна поперечна (и в этой волне колебания полей и — взаимно перпендикулярны).
Рассмотрев таким же образом пару уравнений (6.9), мы пришли бы к аналогичному выводу: волны - и образуют плоскую электромагнитную волну, бегущую вдоль оси, в которой неразрывно связаны между собой (взаимно индуцируют друг друга) поля - и , эта электромагнитная волна также поперечна.
Вернемся к электромагнитной волне - , . Пусть изменения - в волне описываются некоторой функцией 7 : - 7 , а изменения — функцией :. Используя правило дифференцирования сложной функции, найдем:
* 7 , |
, |
|
|
где штрих означает дифференцирование по аргументу . Первое из уравнений (6.8) как раз и связывает между собой производные .- . и . .:
7
Интегрируя последнее равенство, получаем
7
Знак « » в последнем равенстве относится к волне, бегущей слева направо (т. е. к аргументу ), а знак « » к волне, бегущей справа налево (к аргументу ). Произвольная постоянная в последнем равенстве представляет собой некоторое статическое поле, которое нас не интересует, поскольку оно не связано с переменными полями, образующими волну. Полагая поэтому 0, находим
|
|
|
|
|
|
- |
или - |
7 |
! G , (6.12) |
||
|
|
|
|||
|
0! |
|
0 |
||
где 1 110, < <<0. |
|
|
||||||||||||||
|
|
Итак, в бегущей плоской электромагнитной волне поля E |
||||||||||||||
и B в каждый момент времени в каждой точке пространства |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пропорциональны друг |
другу. |
|
y |
|
|
|
|
|
|
v |
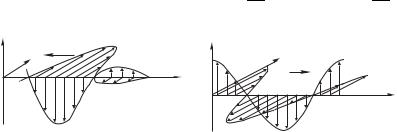
На рис. 6.4 показана «мгновен- |
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ная фотография» — распреде- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ление полей E и B как функ- |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
ции координаты в некоторый |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
момент времени для волны, |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бегущей слева направо. На ри- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сунке показано, что - |
макси- |
|
|
|
|
|
|
|
|
Рис. 6.4 |
мально в данный момент вре- |
|||||||
514 |
Электромагнитные волны |
[ Гл. 6 |
|||
Рассмотрим суперпозицию двух плоских монохроматических |
|||||
волн, бегущих в положительном направлении оси ( -волны |
|||||
и -волны). Колебания в некоторой фиксированной плоскости |
|||||
можно записать в виде |
|
||||
- |
1 1 ; |
- 2 2 , |
|||
где 1 и 2 — амплитуды волн, 1 и 2 — начальные фазы: |
|||||
1 #1, 2 #2. Задача сложения двух взаимно пер- |
|||||
пендикулярных колебаний одинаковой частоты была рассмотре- |
|||||
на в гл. 1.5. Мы выяснили, что в общем случае конец суммарного |
|||||
вектора описывает эллипс, вид которого зависит от амплитуд и |
|||||
разности фаз 2 1 |
слагаемых колебаний. В частных |
||||
случаях 0 и $ результирующая волна оказывает- |
|||||
ся линейно-поляризованной — эллипс вырождается в прямую. |
|||||
Плоскость колебаний суммарного вектора E при 0 ориен- |
|||||
тирована так, как показано на рис. 1.29 б, а при $ — как |
|||||
на рис. 1.29 г. При $ 2 оси эллипса совпадают с осями |
|||||
и (см. рис. 1.29 в). Если, кроме того, 1 2, то получаем |
|||||
круговую поляризацию — конец суммарного вектора описывает |
|||||
окружность |
(см. рис. |
1.29 д). В гл. 1.5 мы |
обсуждали вопрос |
||
о направлении вращения суммарного вектора в фиксированной |
|||||
плоскости . Рекомендуем читателю еще раз вернуться |
|||||
|
|
|
к этому обсуждению. |
||
|
|
|
|
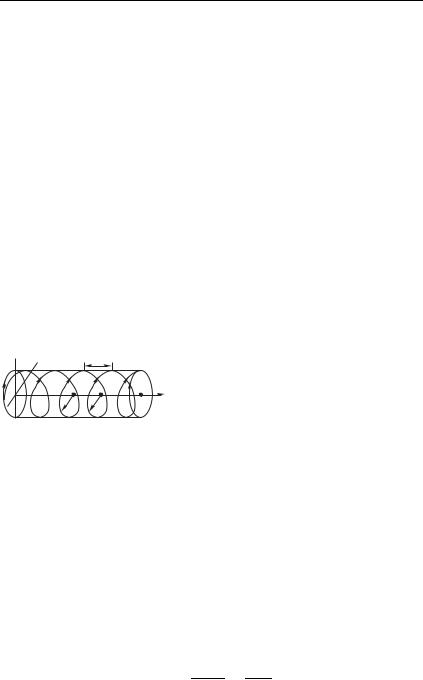
Пространственную структуру эл- |
|
|
|
z |
липтически поляризованной волны |
||
|
|
поясняет рис. 6.7 (на примере вол- |
|||
|
|
|
ны с левой круговой поляризацией). |
||
|
|
|
Винтовая линия, |
изображенная на |
|
Рис. 6.7 |
|
рисунке, есть геометрическое место |
|||
|
|
|
концов суммарного вектора в раз- |
||
личных плоскостях в фиксированный момент времени. Шаг вин- |
|||||
та равен длине волны . С течением времени изображенная |
|||||
на рисунке |
винтовая |
линия |
перемещается, |
не деформируясь, |
|
в направлении распространения волны, вдоль оси . В каждой |
|||||
фиксированной плоскости вектор вращается против |
|||||
часовой стрелки, если смотреть навстречу волне. |
|||||
6.3. Энергетические характеристики электромагнитных волн. Вектор Пойнтинга
Напомним, что электрическое и магнитное поля обладают энергией. В каждой единице объема, заполненного электрическим и магнитным полями, локализована энергия, равная
=эм |
000*2 |
|
2 |
|
(6.14) |
|
2 |
|
2!!0 |
|
|


516 Электромагнитные волны [ Гл. 6
Тогда последнее соотношение примет вид |
|
|||
|
|
|
)эм 91 92 |
(6.17) |
|
||||
Это — частный случай теоремы Пойнтинга (разд. II, гл. 9):
изменение энергии электромагнитного поля в единицу времени обусловлено тем, что через сечение 1 в объем втекает энергия, равная 91, а через сечение 2 из объема вытекает
энергия, равная 92. Таким образом, физический смысл величины 9, которую мы определили равенством (6.16), — это плотность потока электромагнитной энергии, т. е. энергия, протекающая
в единицу времени через единичную площадку, перпендикулярную направлению распространения волны. Обратим внимание, что для -волны, бегущей слева направо, величины - и имеют одинаковый знак, поэтому в этой волне в любой момент времени 9 0 — энергия течет слева направо.
Вектор S, введеный с помощью равенства
, |
(6.18) |
определяет величину и направление потока электромагнитной
энергии и называется вектором плотности потока энергии, или
вектором Пойнтинга.
Рассмотрим поток энергии в волне, бегущей слева направо вдоль оси , которая содержит как -волну, так и -волну. Суммарное электрическое поле этой волны есть
- - ,
где и — единичные орты в направлении осей и соответственно. Магнитное поле волны
G G ,
так как в -волне положительному полю - соответствует отрицательное поле G . Вектор Пойнтинга в сумарной волне есть
- - , G G
Поскольку 0 и 0, то из последнего равенства получаем
9 - G - G 9 9 ,
где 9 и 9 — потоки энергии, которые существовали бы в отдельно взятых -волне и -волне. В частном случае монохроматических волн, используя (6.13), можно получить (упражнение для читателя):
|
1 |
0 |
2 2 |
|
9 |
|
|
-1 -2 , |
(6.19) |
2 |
! |
где 9 — среднее значение потока энергии за период колебания.
6.4 ] |
Стоячая электромагнитная волна |
517 |
6.4. Стоячая электромагнитная волна
Рассмотрим суперпозицию двух бегущих навстречу друг другу гармонических волн одинаковой частоты, амплитуды и поляризации (например, две -волны). В волне, бегущей слева направо:
-1 , |
|
|
|
|
|
1 <1 |
|||||
В волне, бегущей справа налево: |
|||||
-2 , |
|
|
|
||
2 <1 |
|||||
Еще раз подчеркнем, что колебания полей -1 и -2 происхо-
дят вдоль оси , а полей 1 |
и 2 — вдоль оси . Результирующие |
||
поля - и есть |
|
|
|
- -1 -2 2 ; |
|||
|
|
|
(6.20) |
|
|
||
1 2 |
2 0! |
||
|
7 |
|
|
Соотношения (6.20) описывают стоячую электромагнитную волну. Связь между полями - и в этой волне в корне отличается от (6.12) — связи - и в бегущей волне. Напомним, что, согласно (6.12), в любой фиксированной плоскостиколебания полей - и происходят синфазно; там, где в данный момент максимально поле -, там же в этот момент максимально поле (значит, там же в этот момент максимальна плотность электромагнитной энергии и там же максимален и поток энергии). Это — полная аналогия с тем, что происходит в бегущей упругой волне. В стоячей электромагнитной волне колебания - и сдвинуты по фазе на четверть периода:
втот момент времени, когда электрическое поле максимально
вданном месте ( 1), магнитное поле обращается в нуль ( 0) и наоборот. Значит, за четверть периода происходит полное превращение электрической энергии в магнитную и наоборот. Кроме того, пучностям электрического поля ( 1) соответствуют узлы магнитного поля ( 0), т. е. пучности электрического и магнитного полей сдвинуты друг относительно друга на 4 (разумеется, так же сдвинуты друг относительно друга и узлы). Согласно (6.18) поток энергии равен нулю в тех местах, где обращается в нуль либо электрическое поле волны, либо магнитное поле. Следовательно, промежуток пространства, равный 4 (вдоль оси ) — от узла электрического поля до ближайшего узла магнитного поля, не обменивается энергией с соседними участками (сравните с продольной упругой стоячей волной в стержне с закрепленными концами, либо с поперечной волной в натянутой струне). Распределение электрического
518 |
|
Электромагнитные волны |
[ Гл. 6 |
|
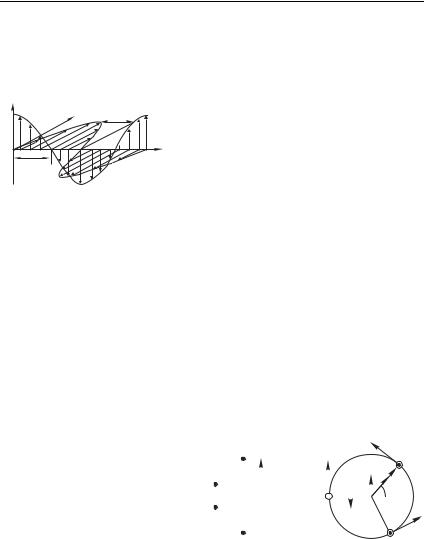
и магнитного полей в стоячей волне вдоль оси (мгновенная |
||||
фотография) показано на рис. 6.8. |
|
|||
Стоячие электромагнитные волны возникают в резонаторе |
||||
Фабри–Перо, образованном двумя параллельными идеально про- |
||||
водящими металлическими стенками. Поскольку на поверхности |
||||
y |
|
идеального проводника тангенциаль- |
||
/4 |
ная компонента электрического поля |
|||
x |
||||
|
|
должна обращаться в нуль, то ситуа- |
||
O |
|
z ция в точности подобна той, которая |
||
|
возникает в стержне с закреплен- |
|||
|
|
|||
/4 |
|
ными концами либо в натянутой и |
||
|
|
закрепленной на концах струне (по- |
||
Рис. 6.8 |
|
скольку аналогичны граничные усло- |
||
|
вия: - 0 - + 0, где + — рас- |
|||
|
|
|||
стояние между проводящими стенками). Возможные частоты ко- |
||||
лебаний определяется соотношением ( 2+ , аналогичным |
||||
(5.25), а возможные типы колебаний |
|
|||
- , 2
полностью аналогичны типам упругих стоячих волн в стержне.
6.5. Излучение колеблющегося диполя
Колеблющийся диполь является простейшей системой, излучающей электромагнитную волну. Модель колеблющегося диполя используется при исследовании излучения многих реальных
излучающих |
систем, |
таких, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
как радиоантенна или даже |
|
|
|
|
E |
|
E |
|
|
|
|
||||||
излучения света атомом. |
|
+q |
|
+q |
|
|
|
|
|
r |
B |
||||||
|
|
|
|
|
|
|
|
|
|||||||||
Практической реализаци- |
|
|
|
|
|
|
|
p |
|
n |
|
|
|||||
|
|
|
|
|
B |
|
|
ψ |
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||
ей диполя является |
элемен- |
U(t) |
l |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||
+ |
|
|
|
|
|
|
|
||||||||||
|
|
O |
|
|
|
|
|||||||||||
тарный |
осциллятор, |
изобра- |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
p |
|
|
|
|
E |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
женный |
на |
рис. 6.9 а: |
два |
−q |
|
−q |
|
|
|
|
|
|
|
|
|
|
|
проводящих |
шарика, |
заряды |
|
|
|
|
|
|
|
|
|
|
|
B |
|||
которых / меняются по гар- |
à |
|
|
|
|
á |
|
|
|
|
|||||||
моническому закону. Это из- |
|
|
|
Рис. 6.9 |
|
|
|
|
|
|
|
||||||
менение |
обеспечивается |
пе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ременным напряжением , , которым питается осциллятор. Дипольный момент такой системы есть, по определению, / , где — вектор, направленный от отрицательного заряда к положительному (см. разд. II).
При гармоническом изменении заряда / /0 имеем
0 , где 0 /0 |
(6.21) |

6.5 ] |
Излучение колеблющегося диполя |
519 |
|
Будем полагать, что размеры осциллятора много меньше дли- |
|
ны излучаемой волны: |
|
|
|
2 7, |
(6.22) |
где — скорость электромагнитных волн: вибратор находится в вакууме. Кроме того, нас будет интересовать излучение диполя на расстояниях от него, больших по сравнению с длиной волны
При выполнении указанных условий диполь называется точечным.
Согласно классическим представлениям, возбужденный электрон в атоме ведет себя как гармонический осциллятор, совершающий колебания относительно положения равновесия. При этом частота колебаний определяется массой электрона и «жесткостью связи» (см., например, модель атома Томсона, гл. 4.1). В результате гармонических колебаний электрона атом приобретает переменный дипольный момент (6.21).
Приведем без вывода формулы, определяющие электрическое и магнитное поля в электромагнитной волне, излучаемой колеблющимся диполем:
1 |
1 |
# |
|
, (6.23) |
||
|
|
|
|
|
|
|
4 00 |
|
73# 7 |
|
|||
Формулы (6.23) определяют поля и в точке наблюдения, отстоящей от середины диполя на расстояние . Единичный вектор n направлен от центра диполя к точке наблюдения
(рис. 6.9 б). Обсудим физическое содержание формул (6.23).
1. Поля и определяются второй производной по времени дипольного момента p (вектором ), т. е. ускорением,
с которым меняется заряд диполя / (либо расстояние между зарядами ): волна излучается лишь ускоренно движущимися зарядами.
2.Поля и на расстоянии от колеблющегося диполя
вмомент времени зависят от значения в более ранний момент времени — запаздывание зави-
сит от времени распространения волны от осцил- E |
B |
|
лятора до точки наблюдения > . |
|
|
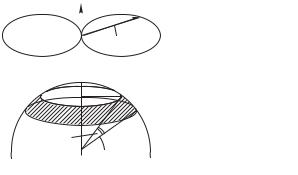
3. Электромагнитная волна, излучаемая дипо- |
|
|
лем, является плоскополяризованной: вектор |
|
|
параллелен вектору , т. е. оси диполя, поэтому |
|
|
вектор перпендикулярен плоскости, в кото- |
|
|
рой лежат векторы и (плоскости рис. 6.9 б); |
Рис. 6.10 |
|
вектор лежит в плоскости рисунка и пер- |
||
|
пендикулярен вектору . Пространственная картина полей и показана на рис. 6.10: линии вектора расположены по
520 |
Электромагнитные волны |
[ Гл. 6 |
меридианам, а линии — по параллелям сферы с центром
вточке, совпадающей с центром диполя.
4.Поля - и убывают при удалении от диполя обратно пропорционально первой степени расстояния 1 (в отличие от
поля статического диполя, которое убывает по закону 1 3 —
т.е. гораздо быстрее).
5.Излучение диполя обладает определенной анизотропией: амплитуды полей зависят от широтного угла B: - и макси-
мальны в направлении B 0 (т. е. на экваторе) и обращаются в нуль на полюсах (B $ 2).
Найдем, используя (6.21), 8 . Имеем 8
280 ; 8 280 . Подставляя последнее выражение в (6.23), найдем
|
2&0 |
|
, |
3# B |
|||
|
4 007 |
|
(6.24) |
|
2&0 |
|
|
- |
|
. |
|
2# B |
|||
|
4 007 |
|
|
Важно подчеркнуть, что на больших расстояниях ( ) волновые поверхности, излучаемые колеблющимся диполем, имеют сферическую форму, а амплитуда колебаний убывает по закону 1 — так же, как в сферической волне, излучаемой точечным источником.
|
Электромагнитная |
энергия, излучаемая |
колеблющимся |
||||||||||||||
диполем. Используя (6.24), |
вычислим поток энергии в точке |
||||||||||||||||
|
|
|
|
|
|
|
, B в волне, излучаемой |
дипо- |
|||||||||
|
P |
|
|
S |
лем. Имеем |
(используя |
формулы |
||||||||||
|
|||||||||||||||||
à |
|
|
|
|
|
|
G 110 и 2 |
1 <010 ): |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
4&2 |
2 B |
|
|
|
|
|
|
|
|
9 -G |
|
|
0 |
|||||||
|
|
|
|
|
|
|
4 200 |
|
73#2 |
|
|||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
rd |
|
|
|
|
|
|
|
2 |
(6.25) |
|||||
|
|
|
|
|
|
|
Направление потока |
совпадает |
|||||||||
á |
|
|
r |
|
|
|
с нормалью n к волновой поверхно- |
||||||||||
|
|
|
|
|
|
сти. Среднее за период значение 9 |
|||||||||||
|
d |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
есть |
|
4&2 |
|
|
2 B |
|
(6.26) |
|||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Рис. 6.11 |
|
|
|
|
9 |
0 |
|
|
|
|||||||
|
|
|
|
|
32 |
20 3#2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
07 |
|
|
|
|
|
|
На рис. 6.11 а показана полярная диаграмма направленности излучающего диполя — зависимость 9 от B (при фиксиро-
ванном ) в полярных координатах. |
2 B) уменьшается с ро- |
||
Поток |
монотонно (по закону |
||
стом угла B от |
максимального |
значения, равного 9 |
|
482 |
32$2<2 |
5 2 при B 0 до нулевого при B $ 2 — |
|
0 |
0 |
|
|
