студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

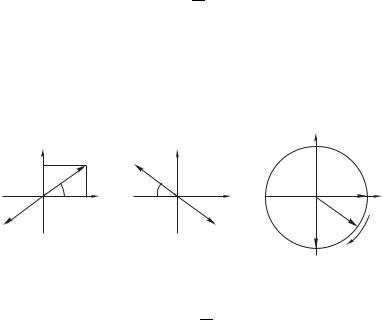
(плоскость наблюдения предполагается фиксированной). Поскольку роль играет лишь относительная разность фаз, то можно, приняв фазу колебаний в начале координат плоскости наблюдения нулевой, записать

, 2 2 2

Используя сделанные приближения, мы, по существу, полагаем, что сферическую форму волнового фронта можно на малом

участке заменить параболической, поэтому приближение (4.17) называется параболическим. В дальнейшем всюду, где это необ-

ходимо, мы будем пользоваться параболическим приближением без каких-либо оговорок.

4.2.Монохроматические волны. Комплексная амплитуда. Уравнение Гельмгольца

Выше мы рассмотрели простейшие примеры монохроматических волн. В самом общем случае уравнение монохроматической волны (не обязательно плоской, сферической или цилиндрической) имеет вид

где — радиус-вектор точки наблюдения.

В любой фиксированной точке наблюдения волна (4.18) создает гармонические колебания частоты с амплитудой и начальной фазой . Функции и определяют пространственную структуру волны, в том числе и форму волновых поверхностей.

При изучении монохроматических волн, так же, как и при изучении гармонических колебаний, удобно использовать комплексную форму записи. Наряду с волной (4.18), рассмотрим волновой процесс вида

му уравнению), то функция (4.19) также описывает волну: ведь (4.19) можно получить из (4.18) просто изменением нача-

ла отсчета времени: 91 , 9 , 4 , где 2$ — период колебания. Ясно также, что линейная комбинация функ-

ций (4.18) и (4.19) вида

также удовлетворяет волновому уравнению. (Линейная суперпозиция решений волнового уравнения (4.5) также является решением.)

484 Кинематика волн [ Гл. 4

Используя параболическое приближение (4.17), имеем

(полагаем 0 0).

4.3. Векторные волны

До сих пор речь шла о скалярных волнах, т. е. о волновом возмущении 9 , , которое описывается скалярной величиной 9. Например, таким образом можно представить звуковые волны, распространяющиеся в воздухе. В этом случае 9 , — изменения плотности или давления — скалярные величины.

Теперь мы рассмотрим кинематику простейших векторных волн: речь будет идти об изменяющейся в пространстве и во времени векторной величине (например, напряженности электрического или магнитного полей в электромагнитной волне).

В общем случае вектор может иметь произвольное направление по отношению к направлению распространения (т. е. по отношению к волновому вектору !). Если вектор параллелен направлению распространения, волна называется продольной.

Если вектор перпендикулярен направлению распространения, волна называется поперечной. Именно особенности структуры

поперечных волн мы здесь рассмотрим.

Наиболее простой тип поперечной волны — так называемая

плоскополяризованная волна (употребляется также термин ли- нейно-поляризованная волна). В плоско-поляризованной волне

волне колебания происходят в плоскости параллельно оси, т. е. вектор не имеет -компоненты (и, конечно, не имеет проекции на направление распространения ).

В общем случае поперечная волна, бегущая вдоль оси , может иметь как -проекцию 9 , так и -проекцию 9 . Рассмотрим ситуацию, когда каждая из проекций представляет собой плоскую гармоническую волну одной и той же частоты:

9 1 #1 , 9 2 #2 , (4.29)

— вновь имеем линейно-поляризованную волну (рис. 4.7 б), однако колебания происходят вдоль прямой, лежащей во втором

ичетвертом квадрантах.

Вобщем случае, как отмечалось, конец вектора описывает эллипс, совершая полный оборот за один период колебаний. Как определить направление вращения вектора? Вернемся

к эллиптически-поляризованной волне, в которой #2 #1 $ 2. Фиксируем плоскость наблюдения и проследим за ориентацией вектора в этой плоскости в различные моменты

времени. Полагая #1 *1 и #2 *2, перепишем (4.29) в виде

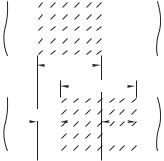
Из последних равенств следует, что в момент времени, когда *1 0, 9 1, 9 0, т. е. вектор S направлен вдоль оси . На рис. 4.7 в его положение в этот момент изображено вектором 1. В последующие моменты времени (когда

0 ' *1 ' $ 2) 0 ' 9 ' 1, а 9 ' 0, т. е. вектор , повернувшись по часовой стрелке, занял положение, показан-

ное на рисунке вектором 2. Далее, при *1 $ 2 имеем 9 0, 9 2 — вектор занял положение, показанное вектором 3.

Итак, мы видим, что вектор вращается по часовой стрел-

ке (с точки зрения читателя, к которому направлен волновой вектор). Это — так называемая правая эллиптическая поляри-

зация. Читатель может самостоятельно убедиться в том, что при

#2 #1 $ 2 направление вращения меняется на противоположное (левая эллиптическая поляризация).

Задачи

1.Напишите выражение для комплексной амплитуды плоской волны, имеющей амплитуду и распространяющуюся под углом 6 к оси (вектор лежит в плоскости ).

2.То же для плоской волны, распространяющейся вдоль оси .

3.Напишите выражение для комплексной амплитуды сферической волны, источник которой находится в начале координат.

4.Докажите, что комплексные амплитуды плоской и сферической волн удовлетворяют уравнению Гельмгольца.

5.Докажите, что функция ( описывает волну, бегущую в направлении оси , при этом функция ( описывает волну, бегущую в противоположном направлении — навстречу оси .

6.Покажите, что расстояние между узлами стоячей волны равно 2.

7.Напишите уравнение монохроматической эллиптически поляризованной волны с правой поляризацией.

8.Каково достаточное условие применимости параболического приближения для сферической волны?

Г л а в а 5

УПРУГИЕ ВОЛНЫ

Мы погружены в океан волн, создающих особый таинственный и чарующий мир звуков: рокот морского прибоя, звучание скрипичной струны, голоса людей — все это волны, рожденные в упругих средах.

В этой главе мы рассмотрим конкретные физические механизмы, приводящие к появлению упругих (акустических) волн в твердых телах, жидкостях и газах.

5.1. Продольные упругие волны в твердом теле

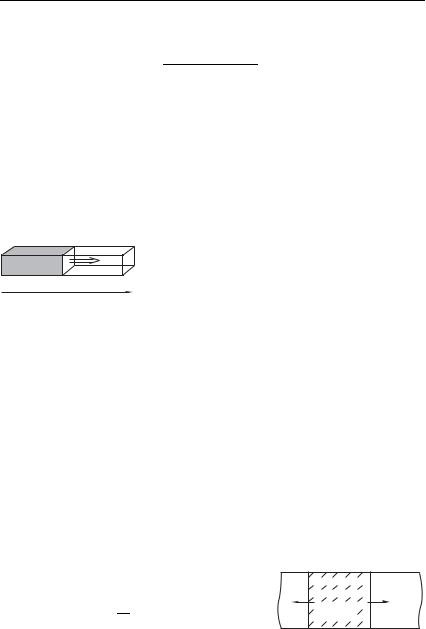
Рассмотрим механизм распространения продольных упругих взаимодействий в стержне. Пусть ось направлена вдоль оси стержня и пусть частицы, составляющие стержень, могут смещаться лишь вдоль оси . Рассмотрим частицы, находящиеся

в положение , а сечение — в положение . Мы имеем

A , A

здесь A — смещение сечения .

Длина рассматриваемого участка изменилась и стала равной, а изменение его длины (удлинение) равно

5.1 ] Продольные упругие волны в твердом теле 489

плотность). Пусть A — смещение центра масс участка стержня, 2A 2 — его ускорение. Мы получаем

2H

309 2 9; 9;

(в правой части равенства — сумма внешних сил, действующих на участок стержня со стороны прилегающих к нему частей стержня справа и слева). Разделив обе части равенства на 9 и перейдя к пределу при 0, находим:

Мы пришли к волновому уравнению, а это означает, что смещение A , распространяется по стержню в виде волн:

Из (5.6) следует, что скорость звука тем больше, чем жестче (больше -) и легче (меньше 30) среда. Например, в стали (-1,96 1010 H/м2, 30 7,7 103 кг/м3) 5 000 м/с, примерно в пять раз больше, чем в свинце.

Если смещение A найдено (т. е. найдено решение (5.5) волнового уравнения), то скорость, с которой движутся различные сечения стержня, найдем, дифференцируя (5.5) по (при фиксированном ):

Следует подчеркнуть, что волна смещений (как и волна деформаций) распространяется вдоль стержня на сколь угодно большие расстояния (в соответствии с (5.5) и (5.8)). Однако сами частицы стержня, находящиеся в любом сечении, смещаются при этом лишь незначительно, приводя в движение частицы соседних сечений, те в свою очередь передают свой импульс соседним частицам и т. д. — именно так малые смещения частиц стержня приводят к распространению волнового возмущения на большие расстояния.

5.2. Упругие волны в жидкостях и газах

Рассмотрим жидкость или газ, заключенный в гладкой цилиндрической трубе. Быстрое (не квазистатическое!) изменение давления в прилегающем к поршню слое нарушают равновесное состояние: давление и плотность в различных сечениях трубы оказываются различными. Является ли процесс распространения возмущений вдоль оси трубы волной?

Рассмотрим слой среды между плоскостями и (см. рис. 5.1). Его ускорение обусловлено разностью давлений в этих сечениях. Пусть давление в плоскости равно 80 8 , а в плоскости давление равно 80 8 . Используя второй закон Ньютона, получаем

21

39 2 9 8 8 ,

где 0 — смещение центра масс участка среды, 20 2 — его ускорение. Разделив обе части равенства на 9 и переходя к пределу при 0, получаем

Перепад давлений приводит не только к ускоренному движе-

8. Будем предполагать, что 8 80.

В общем случае давление является функцией плотности 3 и температуры . В силу малой теплопроводности газов и жид-