Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2777

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.28 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 129 10 11 12 > Следующая >>>


Теорема.	Если несобственный интеграл		f x	dx
		a
сходится, то	сходится и интеграл	f x dx	(без
		a

доказательства).

Геометрически теорему можно пояснить так. Если интеграл сходится абсолютно, то площадь, ограниченная

кривой y	f (x)	при a x	конечна. Значит, будет

конечна и алгебраическая сумма площадей, ограниченных

кривой y	f x .
Если	несобственный	интеграл	f x dx сходится,			а
			a
несобственный интеграл		от модуля	функции		f x	dx
несобственный интеграл		от модуля	функции		f x	dx
				a

расходится, то говорят, что несобственный интеграл сходится

условно.

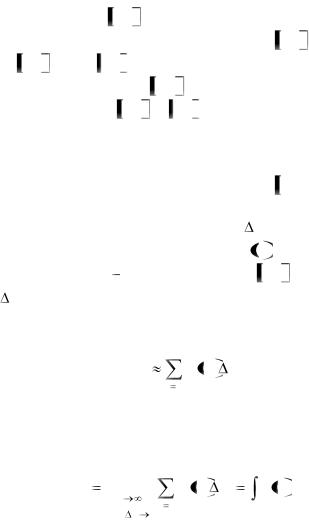
Пример

3.14.

Исследовать

сходимость

интеграла

cos x

dx .

Решение: Рассмотрим интеграл:

cos x

. Сравним его

x 2

со сходящимся интегралом

. Очевидно, что

cos x

x 2

1 x

x 2

cos x

следовательно,

сходится,

а потому

и исходный

x 2

интеграл сходится абсолютно.

Теорема. Если знакопеременная на отрезке a, b функция f xиспытывает разрыв второго рода только в точке

	b
b , и несобственный интеграл		f x	dx от	модуля	этой
b , и несобственный интеграл		f x	dx от	модуля	этой
	a
				b
функции сходится, то сходится также интеграл				f x dx	(без

доказательства).

Вопросы для самопроверки

1.Сформулируйте определение определенного интеграла.

2.Каков геометрический смысл определенного интеграла?

3.Что является достаточным условием интегрируемости функции?

4.Каков физический смысл определенного интеграла?

5.Перечислите свойства определенного интеграла.

6.Какие свойства определенного интеграла связаны с неравенствами?

7.Каков смысл теоремы о среднем для определенного интеграла?

8.О чем говорит теорема Барроу о производной определенного интеграла по переменному верхнему пределу?

9.Выведите формулу Ньютона – Лейбница.

10.Как производится замена переменной в определенном интеграле?

11.Что собой представляет несобственный интеграл первого рода?

12.Дайте определение несобственного интеграла второго

рода.

13.Каков геометрический смысл несобственных интегралов первого и второго рода?

Задачи для самастоятельного решения

Вычислить определенные интегралы

1							xdx									1
1.							xdx					(Ответ:				1		).
1.					x		2	1		2		(Ответ:			4			).
										2
0
0
e1
2.				ln2 xdx (Ответ: e															2 ).
1
	e							dx
3.								dx						(Ответ:										).

											2										2
	1 x 1 ln											x
1
1		1						x	dx																					3
4.		1						x				(Ответ:								1										3	).
4.												(Ответ:								1											).
0		1						x							6															2
0
4							xdx
4															3				2
5.												(Ответ:			3				2				).
5.												(Ответ:											).
1		2						4x							2
1
6.								dx					(Ответ:														).

		3						2 cos x														5
0
7.			sin x cos2 xdx (Ответ:																							2		).
7.			sin x cos2 xdx (Ответ:																					3				).
0																								3
0

2
8.				sin3 xdx (Ответ: 2																					).
8.				sin3 xdx (Ответ: 2															2						).
0																			2
0

		3
9.				arctgxdx (Ответ:																							ln 2 ).

																			3
0																			3
0
		1															e2							5
10.						x 2 e x dx (Ответ:											e2							5					).
10.		1				x 2 e x dx (Ответ:																e							).
																						e

2 dx

11.1 x2 4x 5 (Ответ: 4 ).

2
2							x	2		1 dx
12.							x			1 dx				(Ответ:						3						).

									x																3
1									x																3
1
0									dx
13.									dx						(Ответ: ln 2 ).


							x 2				2x			9
2							x 2				2x			9

4								dx													2
14.								dx					(Ответ:								2			arctg 2 ).
14.								sin2 x					(Ответ:							2				arctg 2 ).
0 1								sin2 x												2
15.		sin						6	x	dx			(Ответ:					5					).
15.		sin							2	dx			(Ответ:					16					).
0									2									16
0
2						sin			1
									1
16.									x	dx (Ответ: 1).
									x
	1						x 2
0	1						x 2
0
Вычислить несобственные интегралы
17.								dx					(Ответ:									).

					x 2				49										14
0
18.		e 3x dx (Ответ:														1	).
18.		e 3x dx (Ответ:															).
0														3
0
19.							dx				(Ответ: ln 2 ).

				x 2					x
1				x 2					x
1
20.		1						ln x			dx (Ответ: интеграл расходится).
20.											dx (Ответ: интеграл расходится).
1								x
1
1							xdx
21.							xdx					(Ответ: 1).



0					1				x 2
1			ln xdx
22.											(Ответ: 1).
22.							x	2			(Ответ: 1).
0							x	2
0

4.ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

4.1.Схемы применения определѐнного интеграла

Практическое применение определенного интеграла связано с нахождением в геометрических или физических задачах аддитивных величин. Аддитивные величины связаны с

некоторым отрезком a, b		изменения независимой переменной
x таким образом, что при разбиении отрезка a, b			точкой c на
части a, c	и c,b	значение аддитивной	величины,
соответствующее отрезку		a, b , равно сумме значений этой
величины на отрезках a, c		и c,b . Существуют два подхода к

практическому применению определѐнного интеграла: метод интегральных сумм и метод дифференциала.

В методе интегральных сумм отрезок a, b разбивается на n частей. Искомая величина A разбивается на n частичных

слагаемых. Каждое частичное слагаемое					Ai	представляется в
виде произведения некоторой функции f					x ,	вычисленной во
внутренней точке ci	i той части отрезка				a, b , на длину этой
части xi . Приближенное значение величины						A записывается
в виде интегральной суммы:
			n
		A	f ci	xi .
			i 1
Точное значение		величины		A		равно пределу
интегральной суммы
			n		b
A	lim		f ci	xi	f	x dx.
	n		i 1		a
			i 1		a
	max	xi	0

В методе дифференциала на отрезке a, b выбирается переменный отрезок a, x . На этом отрезке величина A становится функцией x . Находится главная часть приращения

A ,	соответствующая приращению длины отрезка на x :
dA	f x dx . Искомая величина A находится интегрированием

дифференциала dA в пределах от a до b :

A f x dx.

4.2. Площадь плоской фигуры в декартовых координатах.

Если	f (x) 0	на	отрезке				a, b , то площадь
криволинейной трапеции вычисляют по формуле
			b
		S		f	x dx.
			a
Если	f (x) 0 на	a, b , то
		b				b
	S		f (x)dx				f (x)	dx .
	S		f (x)dx				f (x)	dx .
		a				a
Если f(x) принимает на			a, b		значения разных знаков, то
			b
		S		f (x)		dx
		S		f (x)		dx

Пример 4.1. Вычислить площадь фигуры, ограниченной

линиями:	y		x		, y 0,			x	1,		x		3 (рис.9).

			x2
				1
Решение:
S	3	xdx				1	ln x2	1		3		1	ln10 ln 2	1	ln 5.

	1	x2 1		2						1	2			2

								86

x 2

Рис.9.

Площадь

фигуры,

ограниченной

линиями

1 x ,

x ,

a ,

b ,

если

выполняется

условие

x >

1 x , может быть вычислена по формуле:

2 x

1 x

dx.

Пример.4.2. Вычислить площадь фигуры, ограниченной

линиями y

1. (рис. 10).

Решение:

y y x 1

-1 0	5
	x
y	x2 3x 4

Рис.10.

Для нахождения абсцисс концов отрезка интегрирования приравняем y x2 3x 4 и y x 1. В результате получаем

квадратное уравнение				x2	4x 5			0 , решая которое находим
x1	1 и x2	5 . Тогда
	5				5						x3			5
S	x 1 x 2	3x 4 dx				x 2		4x 5 dx				2x 2	5x	1
S	x 1 x 2	3x 4 dx				x 2		4x 5 dx		3		2x 2	5x
	1				1					3
	1				1
	125		50	25	1		2	5	42	78		36 .

		3			3
		3			3

Рассмотрим случай, когда криволинейная трапеция ограничена кривой, заданной уравнениями в параметрическом виде:

yx , t1 t t2 ,

прямыми x a и x	b и осью Ox , где	(t1 )	a,	(t2 ) b .
Формулу для	вычисления площади		криволинейной
			b
трапеции можно получить из формулы		S	ydx ,	выполнив

замену переменной x

x ,

(t)dt, y

(t) :

(t)

(t)dt .

Пример 4.3. Вычислить площадь фигуры, ограниченной

эллипсом

a cost , 0

2 .

b sin t

Решение:

Вычислим четверть площади эллипса,

когда

x меняется

от 0 до a , в то время как t

меняется от

до 0 .

ydx

b sin t a cost dt

absin2 tdt

sin2 tdt

2	1 cos2t dt	ab t	sin 2t				ab				ab , S
2					2			0				ab.
ab								0				ab.


0	2	2	2		0	2		2		4
0			y		0
			y	Рис. 19
			b
									t	0
			O						a	x
									a

Рис.11.

4.3. Площадь криволинейного сектора в полярной системе координат.

Полярная система координат образуются точкой O , называемой полюсом, полярной осью, представляющей собой луч, выходящий из полюса. Произвольная точка на плоскости характеризуется полярным радиусом , равным расстоянию

от полюса O до точки, а также полярным углом . Полярный угол отсчитывается от полярной оси против часовой стрелки и меняется в пределах от 0 до 2 .

Для выяснения связи полярных и декартовых координат совместим с полюсом начало системы декартовых координат, а ось Ox - с полярной осью (рис.12). Рассмотрим точку M , имеющую декартовы координаты x, y и полярные

координаты , .

Из треугольника на рис 12 следуют формулы перехода от полярных координат к декартовым координатам и наоборот:

cos

y 2 ,

sin

Рис. 12.

Найдѐм площадь криволинейного сектора, ограниченного

линией

f (

)

и двумя

лучами:

выходящими

из

полюса.

Воспользуемся

методом

дифференциалов.

Выделим произвольный

внутренний

угол

, .

Рассмотрим площадь

части указанного криволинейного

сектора, заключенную между углами

. Назначим углу

приращение

d .

=f( )

Рис.

dψ

Рис. 13.

Тогда

приращение

функции

равно

площади

«элементарного

криволинейного сектора»

OBA

(рис.13).

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 129 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.24 Mб02763.pdf
#
15.11.20222.24 Mб22764.pdf
#
15.11.20222.24 Mб22765.pdf
#
15.11.20222.25 Mб02768.pdf
#
15.11.20222.27 Mб02773.pdf
#
15.11.20222.28 Mб22777.pdf
#
15.11.20222.28 Mб02780.pdf
#
15.11.20222.29 Mб02784.pdf
#
15.11.20222.29 Mб12787.pdf
#
15.11.20222.3 Mб02788.pdf
#
15.11.20222.3 Mб32790.pdf