
2777
.pdf
постоянной, то равенство производных от неопределенных интегралов означает равенство и самих неопределенных интегралов.
5. Неопределѐнный интеграл от алгебраической суммы двух функций равен сумме неопределѐнных интегралов от слагаемых функций:
|
f x g x dx |
|
f x dx g x dx . |
|||||
Пусть F |
x |
f |
x |
и G |
x |
g x . Тогда |
|
|
|
|
f |
x |
g x |
dx |
f x |
g x и |
|
f x dx |
g x dx |
f x dx |
g x dx |
f x g x . |
||||
Как было |
отмечено при |
доказательстве |
предыдущего |
|||||
свойства, равенство производных от неопределенных интегралов означает и равенство самих неопределенных интегралов.
|
6. Если |
|
f x dx F x |
C , то и |
f u du |
F u |
C , где |
||||||
u |
x |
произвольная |
функция, |
имеющая |
непрерывную |
||||||||
производную |
(Свойство |
|
инвариантности |
формулы |
|||||||||
интегрирования). |
|
|
|
|
|
|
|
|
|
||||
|
Пусть |
x |
независимая |
переменная, f |
x |
непрерывная |
|||||||
функция, |
F x |
первообразная |
непрерывной |
функции |
f x , |
||||||||
u |
x |
непрерывно-дифференцируемая |
функция. |
Для |
|||||||||
сложной |
функции |
F u |
F |
x |
в |
силу |
инвариантности |
||||||
формы первого дифференциала имеем |
|
|
|
|
|||||||||
|
|
|
|
|
dF u |
F |
u du |
|
f u du . |
|
|
||
|
Тогда |
f u du |
d F u |
|
F u |
C . |
|
|
|
||||
Формула для неопределенного интеграла не меняется в зависимости от того, что используется в качестве переменной интегрирования, независимая переменная или любая ее непрерывно-дифференцируемая функция.
21
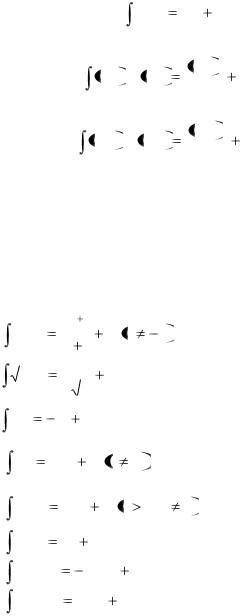
Так, из формулы x5dx |
x6 |
|
||
|
C , поменяв x |
на tgx , |
||
6 |
||||
|
|
|
||
получим
tgx 5 d tgx |
tgx 6 |
C , или, |
|
6 |
|||
|
|
поменяв x на ln x , получим
ln x 5 d ln x |
ln x 6 |
C . |
|
6 |
|||
|
|
2.3. Таблица неопределѐнных интегралов
Пользуясь тем, что интегрирование есть операция обратная дифференцированию, можно получить таблицу основных интегралов с помощью обращения формул для производной конкретных функций и использовния свойства неопределенного интеграла:
|
xa dx |
|
|
|
|
xa 1 |
|
1 ; |
||||||||||||
1. |
|
|
|
|
|
|
|
|
|
|
|
|
c |
a |
||||||
|
|
a |
|
|
1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2. |
|
|
|
|
|
1 |
|
|
|
|
; |
|
||||||||
|
|
xdx |
|
|
|
c |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
x |
|
|
||||||||
3. |
dx |
1 |
|
|
|
|
c ; |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x 2 |
|
x |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
4. |
|
dx |
ln |
|
x |
|
|
|
|
c x |
|
0 ; |
||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
a x |
|
|
|
|
|
|
|||||||
5. |
a x dx |
|
|
|
|
|
|
|
c |
a |
0; a 1 ; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
ln a |
|
|
||||||||
6. |
e x dx e x |
|
|
|
|
c ; |
|
|
||||||||||||
7. |
sin xdx |
|
|
cos x |
|
c ; |
||||||||||||||
8. |
cos xdx |
sin x |
c ; |
|||||||||||||||||
22
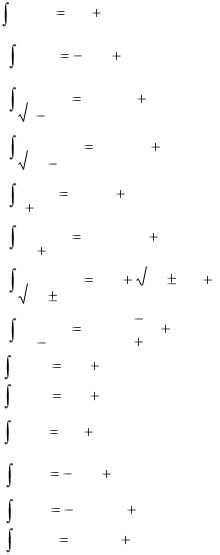
9. |
|
dx |
|
|
tgx c ; |
|
|
|
|
|
|||
cos2 |
x |
|||||
|
|
|||||
10. |
|
dx |
ctgx c ; |
|||
|
|
|
|
|||
|
sin2 |
x |
||||
|
|
|
||||
11. |
|
|
|
|
dx |
|
|
|
|
|
|
arcsin x |
|
|
|
|
c ; |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
|
|
x2 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
12. |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
arcsin |
x |
|
|
c ; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
||||||||||||||||
|
|
|
|
a |
2 |
|
|
|
x |
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
13. |
|
|
|
|
dx |
|
|
|
arctgx c ; |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 |
|
x2 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
14. |
|
|
|
|
dx |
|
|
|
|
|
|
|
1 |
arctg |
x |
|
c ; |
|||||||||||||||
|
|
|
a 2 |
|
|
x2 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|
||||||||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
x |
|
|
|
x2 |
a2 |
c ; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
x2 |
a2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
16. |
|
|
|
|
dx |
|
|
|
|
|
|
1 |
ln |
x |
|
|
|
a |
|
c ; |
||||||||||||
|
|
|
x2 |
|
|
a2 |
|
|
|
|
|
2a |
x |
|
|
|
a |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
17. |
shxdx |
chx |
c ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
18. |
chxdx |
shx |
c ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
19. |
|
|
|
dx |
|
|
|
|
tgx |
|
|
|
|
c ; |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
ch 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
20. |
|
|
|
dx |
|
|
|
|
|
|
|
ctgx |
|
c ; |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
sh2 x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
21. |
|
tgxdx |
|
|
|
ln |
cos x |
|
|
|
c ; |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
c . |
|
|
|
|||||||||||||||||||||
22. |
|
ctgxdx |
|
|
|
ln |
sin x |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все эти формулы проверяются дифференцированием правой части. Например, проверим формулу 12:
23
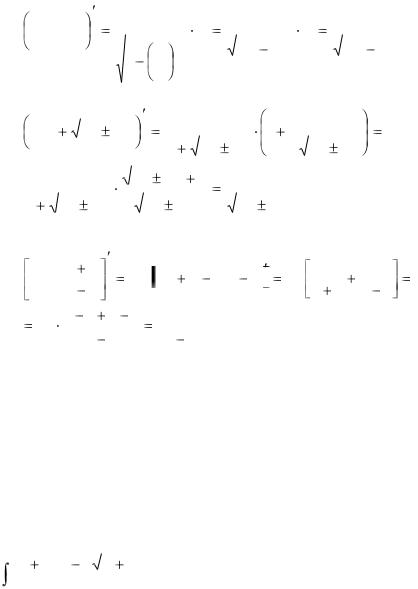
|
|
arcsin |
x |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 a |
|
|
|
|
|
|
x 2 a |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
a 2 |
a 2 |
x 2 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Проверим формулу 15: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
||||||||
|
|
ln |
x |
|
|
|
|
|
|
x2 |
|
a 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
a 2 |
|
|
|
|
x2 |
a 2 |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
a 2 x |
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
x2 |
a 2 |
|
|
|
|
|
|
|
|
|
x2 |
a 2 |
|
|
x2 |
a 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Проверим формулу 16: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
a x |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
ln |
|
|
|
|
|
ln |
a x |
|
ln |
a x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
2a |
a x |
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a a x a x |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
a |
x |
a x |
|
|
|
|
1 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2a |
|
|
|
|
a 2 |
x 2 |
|
a 2 |
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Следует отметить, что в таблице основных интегралов вместо переменной интегрирования x может быть использована непрерывно-дифференцируемая функция переменной x .
В простых случаях неопределенный интеграл с помощью тождественных преобразований подынтегральной функции и использования свойств интеграла приводится к одному или нескольким табличным интегралам, что называется
непосредственным интегрированием.
Пример |
2.1. Найти неопределенный интеграл |
||
|
|
|
|
x7 2x 4 x x |
9 |
dx . |
|
x 2 |
|
||
|
|
||
Решение: |
|
|
|
24

|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x7 2x 4 x x 9 |
|
|
x5 |
2x 2 |
9x 2 dx x5 dx |
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
dx |
x 2 |
|
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
x6 |
|
2x3 |
|
|
|
|
|
|
|
x 1 |
|
|
|
|||
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
||||||||||||
2 x2 dx x 2 dx 9 x 2 dx |
|
|
|
|
9 |
c . |
|
|||||||||||||||||
6 |
3 |
|
1 |
|
|
1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
2.4 Замена переменной в неопределенном интеграле |
|||||||||||||||||||||||
|
Одним из основных методов интегрирование является |
|||||||||||||||||||||||
метод замены переменной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Теорема. Пусть функция t |
|
|
x |
|
непрерывна |
и |
|||||||||||||||||
дифференцируема, |
а |
функция |
g t |
непрерывна |
и имеет |
|||||||||||||||||||
первообразную G t |
, |
т.е. G |
|
t |
g t |
или |
|
g t dt |
G t |
C , |
||||||||||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
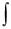 g
g x
x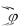
 x dx G
x dx G x
x C .
C .
Доказательство:
Возьмем производную от правой части равенства по x , воспользовавшись правилом дифференцирования сложной функции:
G x
x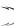 C
C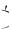 G
G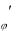
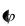
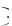
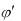 x
x g
g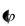
 x .
x .
Поскольку производная оказалась равна подынтегральной функции, т.е. производные правой и левой части равенства совпали, то в исходном равенстве левая и правая части могут отличаться только на постоянную величину, что и требовалось доказать.
Пример 2.2. Найти |
esin x cos xdx. |
Решение: Пусть t |
sin x , тогда dt cos xdx. Тогда |
esin x cos xdx et dt et |
C esin x C . |
25
Как отмечалось выше, вид неопределѐнного интеграла не зависит от выбора аргумента интегрирования, что используется при интегрировании способом введения новой функции под знак дифференциала. В данном варианте метода новая переменная интегрирования не обозначается новым символом, а берется в скобки для наглядности.
Пример 2.3. Найти |
|
ln x |
dx . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ln x |
dx |
ln x |
dx |
|
|
ln x d ln x |
|
ln x 2 |
C . |
|
||||||||||
|
x |
x |
|
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 2.4. Найти |
|
|
sin x cos xdx. |
|
|
|
|
|
|
||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
sin x |
3 / 2 |
|
|
|||||
|
|
sin x cos xdx |
sin x 2 d sin x |
|
C . |
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
3 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Часто замена переменной выполняется в виде x |
t . |
||||||||||||||||||||
Тогда dx 
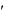 t dt и
t dt и
f x dx |
f |
t |
t dt . |
Доказательство формулы производиться по аналогии с предыдущим посредством взятия производной от обеих частей:
f x dx |
|
f x dx |
x |
x t |
f x |
t |
f |
t |
t |
|
|
t |
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
f |
t |
t dt |
f |
t |
|
t . |
|
|
|
|
Поскольку производные двух функций тождественно равны, то сами функции отличаются на постоянное слагаемое
C .
26

|
|
|
|
Пример 2.5. Вычислить интеграл |
|
|
|
|
|
x 2 |
|
dx. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(x |
3)2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Решение: |
Положим |
|
x |
3 |
|
t , |
|
|
тогда |
x |
|
t |
3. |
|
Отсюда |
|||||||||||||||||||||||||||||||||||||||
dx |
dt . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
t |
3 |
|
2 |
|
|
|
|
|
|
|
|
6 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
dx |
|
|
|
dt |
|
|
1 |
|
|
dt |
t |
|
6 ln |
t |
|
|
C. |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
x |
3 2 |
|
|
|
t 2 |
|
|
|
|
t |
|
t 2 |
|
t |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Возвращаясь к переменной x , окончательно получаем |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 |
|
|
dx x 1 6 ln |
|
x 1 |
|
|
|
|
9 |
|
|
|
|
|
C. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x 3 2 |
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
Пример 2.6. Вычислить интеграл |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
e x |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Решение: |
Обозначим |
|
e x |
t , |
|
|
Тогда |
x |
|
lnt, |
dx |
dt |
. |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
d t |
1 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
e x |
|
2 |
|
|
t |
2 |
|
|
|
t t |
|
2 |
|
|
|
|
t 2 |
|
2t 1 1 |
|
|
|
t 1 2 |
1 |
|
|
|||||||||||||||||||||||||||||||
1 |
|
ln |
|
t 1 |
1 |
|
|
|
C |
1 |
|
ln |
|
|
|
t |
|
|
C |
1 |
ln |
|
|
|
|
e x |
|
|
|
|
C . |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2 |
|
|
|
t 1 1 |
|
|
|
|
2 |
t |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2.5. Правило интегрирования по частям |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Пусть функции u |
|
|
|
u x |
|
и v |
|
v x |
имеют непрерывные |
|||||||||||||||||||||||||||||||||||||||||||||
производные. Тогда d uv |
|
vdu |
udv . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
Интегрируя обе части равенства по x , имеем: |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
d uv |
|
|
|
vdu |
udv , uv |
|
vdu |
|
|
udv или |
udv |
uv |
|
vdu . |
||||||||||||||||||||||||||||||||||||||
27
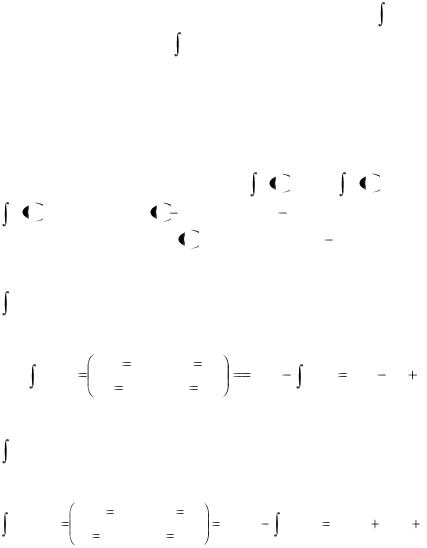
Эта формула называется формулой интегрирования по частям. Формула сводит вычисление интеграла udv к
вычислению интегралов vdu и 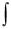 dv , которое может оказаться
dv , которое может оказаться
проще исходного.
Интегрирование по частям требует представление подынтегрального выражения в виде произведения множителей u и dv . Существуют три типа интегралов, в которых по разным соображениям происходит выбор множителей u и dv в подынтегральных выражениях.
В интегралах |
первого |
типа |
P x ekx dx , |
P x sin kxdx , |
|||||||
P x coskxdx, где |
P x |
многочлен, k |
число, |
в качестве |
u |
||||||
выбирается многочлен |
P x , |
а в качестве dv |
все остальные |
||||||||
сомножители. |
|
|
|
|
|
|
|
|
|
|
|
Пример |
|
2.7. |
Вычислить |
неопределенный |
интеграл |
||||||
xex dx , используя метод интегрирования по частям. |
|
|
|||||||||
Решение: |
|
|
|
|
|
|
|
|
|
||
xex dx |
|
u |
x |
du |
dx |
xex |
e x dx |
xex |
e x |
C. |
|
dv e x dx v e x |
|||||||||||
|
|
|
|
|
|
||||||
Пример |
|
2.8. |
Вычислить |
неопределенный |
интеграл |
||||||
x cos xdx. |
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
||
x cos xdx |
u |
x |
du dx |
x sin x |
sin xdx x sin x |
cos x |
C. |
||||
|
|
|
|
||||||||
dv |
|
cos xdx v |
sin x |
|
|
|
|
|
|
||
В некоторых интегралах приходится несколько раз интегрировать по частям.
28

Пример 2.9. Вычислить неопределенный интеграл
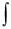 x2e x dx .
x2e x dx .
Решение:
x 2 e x dx |
|
|
u |
|
x 2 , |
du |
|
2xdx |
x 2 e x |
|
|
2xex dx. |
|||||||||||
|
|
dv |
e x dx, |
v |
|
e x |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Применим ко второму интегралу еще раз формулу |
|||||||||||||||||||||||
интегрирования по частям |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x2e x |
2xex dx |
|
u |
2x, |
|
|
|
|
du |
|
2dx |
x2e x |
2xex |
||||||||||
|
dv |
e x dx, |
|
v |
|
e x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 e x dx x2e x |
|
2xex |
2e x |
C. |
|
|
|
|
|
|
|
|
|||||||||||
В |
|
интегралах |
второго |
|
|
типа |
|
P x arcsin xdx, |
|||||||||||||||
P x arccos xdx , P x ln xdx , |
|
P x arctgxdx, |
|
|
P x arcctgxdx |
||||||||||||||||||
удобно |
положить |
dv P x , |
|
а |
|
в |
|
качестве |
|
u |
выбрать |
||||||||||||
оставшиеся сомножители. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример |
|
2.10. |
|
Вычислить |
|
неопределенный |
интеграл |
||||||||||||||||
x4 ln xdx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
u |
|
ln x, du |
dx |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 |
|
|
|
x5 |
|
|
||||
x 4 ln xdx |
|
x |
|
|
|
ln x |
|
|
dx |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
dv |
x 4 dx, v |
|
x5 |
|
|
5 |
|
5 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x5 |
|
|
x6 |
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5 |
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В интегралах третьего вида |
|
eax sinbxdx, |
|
|
eax cosbxdx в |
||||||||||||||||||
качестве |
|
u |
|
|
выбирается |
|
eax . |
|
После |
|
|
двукратного |
|||||||||||
интегрирования по частям решается уравнение относительно исходного интеграла.
29

Пример 2.11. |
|
Вычислить |
неопределенный |
интеграл |
|||
e x sin xdx . |
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
e x sin xdx |
u e x , |
du |
e x dx |
e x cos x |
|
||
dv |
sin xdx, v |
cos x |
|
||||
|
|
|
|||||
e x cos xdx |
u |
e x , |
du |
e x dx |
e x cos x |
e x sin x |
|
dv |
|
cos xdx, v |
sin x |
||||
|
|
|
|
||||
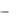 e x sin xdx.
e x sin xdx.
Получили нетривиальный результат-уравнение относительно исходного интеграла. Обозначив его за J , получим уравнение
J |
e x sin x cos x |
J . |
|
|||
Перенося J в левую часть уравнения, имеем |
|
|||||
2J |
e x sin x |
cos x . |
|
|||
Окончательно: e x sin xdx |
e x |
sin x |
cos x |
C . |
||
|
2 |
|
|
|||
|
|
|
|
|
|
|
2.6. Интегрирование рациональных функций. Понятие о рациональных функциях.
Многочленом степени n (или |
целой рациональной |
|||||||
функцией) называется функция вида |
|
|
|
|
||||
P x a |
a x |
a |
2 |
x2 |
... a |
n |
xn |
, |
n |
0 1 |
|
|
|
|
|
||
где n натуральное число, называемое степенью многочлена, ai постоянные коэффициенты, i 0,1,..., n.
30
