
2777
.pdf
Корнем многочлена Pn x называется такое значение x0 (действительное или комплексное) переменной x , при котором
называется такое значение x0 (действительное или комплексное) переменной x , при котором
многочлен обращается в нуль, т.е. |
Pn |
x0 |
|
0 . Следовательно, |
||||||||||
корни |
многочлена |
Pn |
x |
представляют |
собой |
решения |
||||||||
алгебраического уравнения n ой степени: |
|
|
|
|||||||||||
|
|
|
|
|
|
|
Pn |
x |
0. |
|
|
|
|
|
|
Теорема |
Безу: |
Если |
x1 |
является |
корнем многочлена |
||||||||
Pn x , то многочлен делится без остатка на двучлен x |
x1 , |
|||||||||||||
т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn x |
x x1 Pn 1 x , |
|
|
|
|||||
где |
Pn 1 |
x |
многочлен |
степени |
n |
1 . |
Теорема приводится |
|||||||
без доказательства. |
|
|
|
|
|
|
|
|
|
|
||||
|
Всякий ли многочлен имеет корень? Ответ дает основная |
|||||||||||||
теорема алгебры. |
|
|
|
|
|
|
|
|
|
|
||||
|
Основная теорема алгебры: Всякий многочлен степени |
|||||||||||||
n |
имеет, |
по |
крайней |
мере, |
один |
действительный |
или |
|||||||
комплексный корень (без доказательства). |
|
|
|
|||||||||||
|
Важнейшим следствием |
основной |
теоремы |
алгебры |
||||||||||
является терема о разложении многочлена на линейные множители.
Терема о разложении многочлена на линейные
множители: Всякий многочлен |
Pn |
x |
можно представить в |
||||
виде |
|
|
|
|
|
|
|
Pn |
x |
an x |
x1 |
x |
x2 |
... x |
xn , |
где x1 , x2 ,…, xn корни многочлена, |
an |
коэффициент при |
|||||
xn . |
|
|
|
|
|
|
|
Доказательство: Рассмотрим многочлен Pn x , имеющий |
|||||||
корень x1 . Тогда Pn |
x |
x |
x1 Pn 1 |
x . Многочлен Pn 1 x по |
|||
основной теореме |
алгебры |
имеет |
хотя бы один корень, |
||||
31

например x2 . |
Тогда по теореме Безу Pn 1 x |
x x2 Pn 2 |
x , а |
||
Pn x |
x x1 |
x x2 Pn 2 x . Не важно, |
совпал ли корень |
x1 с |
|
корнем |
x2 , |
являются ли они |
комплексными |
или |
|
действительными. Повторяя рассуждения, получим в итоге:
|
|
Pn |
x an |
x |
x1 x x2 |
... x |
xn . |
|
|
|||
Если |
в |
разложении |
многочлена |
Pn |
x |
на |
линейные |
|||||
множители |
x |
xi |
какой-нибудь корень встречается k |
раз, то |
||||||||
корень называется |
|
корнем |
кратности |
|
k . |
Если |
корень |
|||||
встретился один раз, что происходит при |
k |
1 , |
то |
корень |
||||||||
называется простым. |
|
|
|
|
|
|
|
|
||||
С учетом кратности корней разложение многочлена |
||||||||||||
можно записать в виде |
|
|
|
|
|
|
|
|
||||
|
|
P |
x a |
n |
x |
x k1 |
x |
x |
k2 |
... x x |
kr , |
|
|
|
n |
|
|
1 |
|
|
2 |
|
|
n |
|
где r |
число различных корней, корень x1 |
имеет кратность k1 , |
||||||||||
корень |
x2 |
кратность |
|
k2 |
и |
т. |
|
д. |
|
Существенно, что |
||
k1 k2 |
... |
kr |
n . |
|
|
|
|
|
|
|
|
|
Используя теорему о разложении многочлена на линейные множители можно доказать несколько теорем, которые приводятся без доказательства.
Теорема 1. Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого многочлена.
Теорема 2. |
Если |
многочлен Pn |
x с действительными |
коэффициентами |
имеет |
комплексный |
корень a ib , то он |
имеет и сопряженный корень a ib . |
|
||
Последняя теорема говорит о том, что если коэффициенты многочлена действительны, то комплексные корни входят сопряженными парами. Перемножив линейные множители
x a ib x a ib |
x a 2 b2 x2 2ax a 2 b2 , |
32

получим квадратный трехчлен с действительными коэффициентами и отрицательным дискиминантом, который можно записать в виде
x2 px q ,
где p 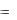 2a, q a2 b2 . Следовательно, объединяя скобки,
2a, q a2 b2 . Следовательно, объединяя скобки,
соответствующие комплексно-сопряженными корнями многочлен степени n с действительными коэффициентами можно разложить только на линейные и квадратичные действительные множители:
P x |
a |
n |
x |
x k1 |
x |
x |
k2 |
... x 2 |
p x |
q S1 |
x 2 |
p |
2 |
x |
q |
S2 ... |
n |
|
|
1 |
|
|
2 |
|
1 |
1 |
|
|
|
|
2 |
,
где все трѐхчлены не имеют действительных корней. При этом
k1 |
k2 |
... |
2 s1 |
s2 |
... n . |
Пример 2.12. Разложить на множители многочлен |
|||||
|
x5 |
4x4 |
4x3 |
x2 |
4x 4 . |
Решение: |
|
|
|
|
|
x5 4x4 4x3 x2 |
4x 4 x3 x2 |
4x 4 x2 4x 4 |
|||
x2 4x 4 x3 1 |
|
x 2 2 x 1 x2 |
x 1 . |
||
2.7. Дробно-рациональные функции. Простейшие рациональные дроби и их интегрирование
Дробно - рациональная функция или рациональная дробь
R x
|
P |
x |
|
|
a |
0 |
a x |
a |
2 |
x2 |
... |
a |
n |
xn |
|
R x |
n |
|
|
|
|
1 |
|
|
|
|
|
|
|||
Qm |
x |
|
|
b0 |
b1 x |
b2 x2 |
... |
bm xm |
|||||||
|
|
|
|||||||||||||
называется правильной, |
если степень числителя n меньше |
||||||||||||||
степени знаменателя m . |
Если n |
m , то рациональная дробь |
|||||||||||||
называется неправильной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
33

Всякую неправильную дробно-рациональную функцию путѐм деления числителя на знаменатель всегда можно представить, в виде суммы многочлена N x и правильной рациональной дроби:
R x N x |
Pk |
x |
k m . |
|
Qm x |
||||
|
|
|||
Пример 2.13 Представить неправильную рациональную
x3
дробь в виде суммы целой части от деления x 2 1
(многочлена) и правильной рациональной дроби Решение: Разделив числитель на знаменатель, выделим
целую часть:
|
|
|
x3 |
|
|
|
x2 |
1 |
|
|
|
|
|
x3 |
x |
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
||
|
|
|
|
x3 |
x |
|
x |
|||
В результате получим |
|
|
|
|
|
. |
||||
x 2 1 |
x 2 1 |
|||||||||
Интегрирование многочлена не представляет труда, поэтому рассмотрим интегрирование правильной рациональной дроби.
Среди правильных рациональных дробей можно выделить четыре типа дробей, называемых простейшими:
|
A |
|
A |
|
Ax B |
|
|
|
|
Ax |
B |
|
|||
1. |
|
, 2. |
|
, 3. |
|
|
|
, 4. |
|
|
|
, |
|||
x a |
x a k |
x2 |
px q |
x2 |
px q k |
||||||||||
где A, B, p, q |
действительные числа, а трѐхчлен |
x2 px q |
|||||||||||||
имеет отрицательный дискриминант, т.е. |
|
p2 |
|
q |
0 . |
|
|
||||||||
4 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Простейшие дроби интегрируются несложным образом:
34
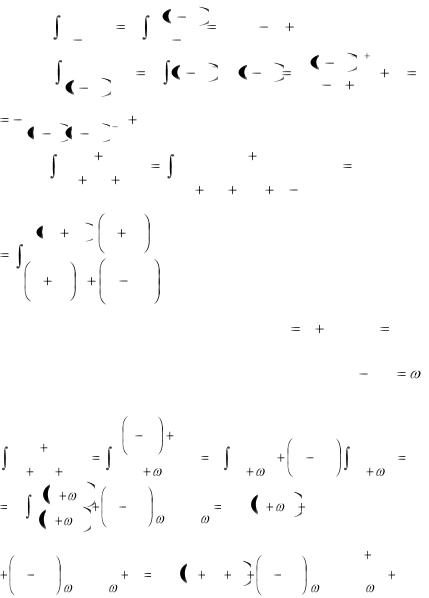
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
d x a |
|
|
|
|
|
|
C , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1. |
|
|
|
|
|
|
dx A |
|
Aln |
x a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a k 1 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
2. |
|
|
|
|
|
|
A |
|
dx A x a |
k d x a A |
|
|
C |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x |
a k |
|
|
|
|
|
|
|
k |
|
|
1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
C, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
k |
1 x |
a k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
3. |
|
|
|
|
|
Ax |
|
B |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax |
B |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
x 2 |
|
|
|
px |
|
|
q |
|
|
|
|
|
|
|
|
|
x 2 |
px |
|
p 2 |
|
q |
|
p 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Ax |
|
|
|
|
B d x |
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x |
|
p |
|
|
|
q |
|
|
|
|
|
|
p 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Произведем |
|
|
|
замену |
переменной |
|
t x |
|
|
|
|
|
p |
|
, |
|
|
dt |
|
dx, и |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
обозначим положительную постоянную величину q |
|
|
p |
2 |
2 . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В результате получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A t |
|
p |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
Ax |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tdt |
|
|
|
|
|
|
|
|
|
Ap |
|
|
|
dt |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
A |
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x2 |
px q |
|
|
|
|
|
|
|
|
t 2 |
2 |
|
|
t |
2 |
|
2 |
|
|
|
|
2 |
|
|
|
t |
2 |
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
A d t 2 |
|
|
|
|
2 |
|
|
|
B |
|
|
|
|
Ap |
|
|
|
|
1 |
|
arctg |
t |
|
A |
ln t 2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
|
|
|
t 2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
Ap |
|
|
1 |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ap |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
B |
|
|
arctg |
|
|
|
|
C |
|
|
|
ln x 2 |
px q |
B |
|
|
|
|
|
arctg |
2 |
|
|
C. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
35
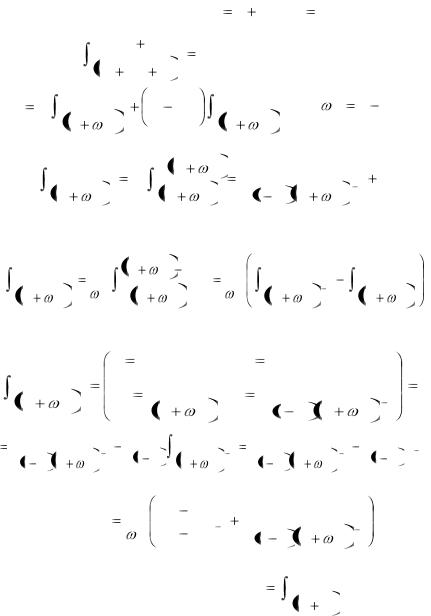
4. Простейшие дроби четвертого типа сводятся с
помощью замены переменной t x |
p |
, |
dt dx к сумме двух |
||||
2 |
|||||||
|
|
|
|
|
|
||
интегралов |
Ax |
B |
|
|
|
||
|
|
|
|
|
|
||
x2 px |
q k |
|
|
|
|||
|
|
|
|
||||
|
|
|
|
|
tdt |
|
|
|
|
|
Ap |
|
|
|
dt |
|
|
|
2 |
|
|
|
p 2 |
|||||
A |
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
, где |
|
q |
|
|
. |
||||
|
t |
2 |
2 k |
|
|
|
|
2 |
|
|
t |
2 |
|
2 k |
|
4 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Первый интеграл легко вычисляется: |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
tdt |
|
|
1 |
|
d t 2 |
2 |
|
|
|
|
|
|
1 |
|
|
|
C . |
|||||||
|
t |
2 |
|
2 k |
2 |
|
t |
2 |
|
|
2 k |
|
|
2 1 |
k |
t |
2 |
2 k 1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При вычислении второго интеграла, который обозначим как I k , используются рекуррентные соотношения:
|
|
|
|
dt |
|
|
|
1 t 2 |
2 |
|
|
t 2 |
|
dt |
|
1 |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
t |
2 dt |
|
|
|
. |
|||||||||||||
|
|
t 2 |
2 k |
|
|
2 |
|
|
|
|
t 2 |
|
2 k |
|
|
|
2 |
|
|
|
|
|
t 2 |
|
|
2 k 1 |
|
|
|
t 2 |
|
|
2 k |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
Последний интеграл найдем с помощью интегрирования |
|||||||||||||||||||||||||||||||||||||||||||||
по частям: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
t 2 dt |
|
|
|
u |
|
t, |
|
|
|
|
|
|
|
|
|
|
du |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
t |
2 |
|
2 k |
|
|
|
dv |
|
|
|
|
|
|
|
, v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
t |
2 |
|
|
|
2 |
k |
2 1 |
|
k |
t |
2 |
|
|
|
2 k |
1 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
t |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
1 |
|
|
Ik 1. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 1 |
k t |
2 |
|
2 k 1 |
2 1 k |
|
|
|
t |
2 |
|
|
|
2 |
k 1 |
2 1 |
k |
t |
2 |
|
|
2 k 1 |
|
2 1 k |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
В результате получим рекуррентное соотношение: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
I k |
1 |
|
2k |
|
3 |
I k 1 |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2k 2 |
|
2 k |
1 t |
2 |
|
|
2 k 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Пример 2.14. Найти интеграл I3 |
|
|
|
|
dt |
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
t 2 |
|
9 3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
36
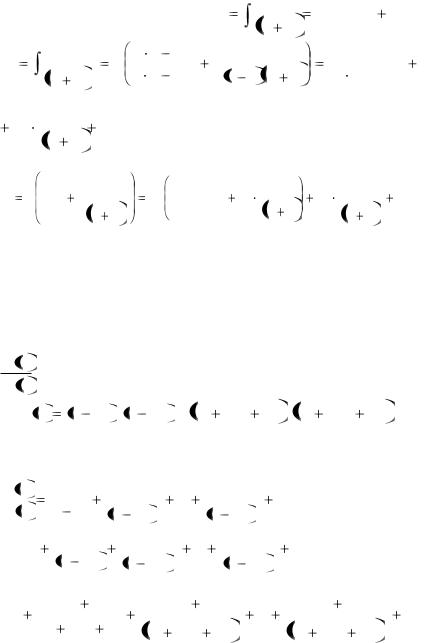
|
|
|
Решение: |
|
Поскольку |
I1 |
|
|
|
dt |
1 |
arctg |
t |
|
C , а |
||||||||||||||||||||||||||||||
|
|
t 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
3 |
|
|
|
3 |
|
|
|
|||||
I 2 |
|
|
|
|
dt |
|
|
1 |
|
|
2 2 |
|
3 |
I1 |
|
|
|
|
|
t |
|
|
|
1 |
arctg |
t |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
t |
2 |
|
9 |
2 |
|
9 |
|
|
2 2 |
|
2 |
2 2 |
|
1 t 2 |
9 |
|
|
18 3 |
3 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
|
|
t |
|
|
|
C, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
18 |
|
|
|
t 2 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
3 |
|
|
|
|
|
|
t |
|
|
|
|
1 |
|
1 |
|
|
t |
1 |
|
|
t |
1 |
|
|
|
t |
|
|
|
|||||||||||||
I3 |
|
|
|
|
I |
2 |
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C . |
|||||||||||||||
9 |
4 |
|
4 t 2 |
9 2 |
|
12 |
54 |
3 |
18 t 2 |
9 |
|
|
36 t 2 |
9 2 |
|
||||||||||||||||||||||||||||||
2.8. Разложение правильной дробно–рациональной функции на сумму простейших дробей.
Теорема: Всякую правильную рациональную дробь
P x , знаменатель которой разложен на множители
Q x
Q x |
x x k |
x |
x |
l ... x2 |
p x |
q S |
x2 |
p |
2 |
x |
q |
p |
..., |
|
1 |
|
|
2 |
1 |
1 |
|
|
|
|
2 |
|
можно представить и притом единственным образом в виде следующей суммы простейших дробей:
P x |
|
|
A1 |
|
|
A2 |
|
|
|
... |
|
|
Ak |
|
|
|
|
||
Q x |
|
x x1 |
x x |
2 |
|
|
|
x x |
k |
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
B1 |
|
|
B2 |
|
|
... |
|
|
Bl |
|
... |
|||||
|
|
|
x x2 |
|
x |
x2 |
2 |
|
|
x |
x2 |
l |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
M1 x N1 |
|
M 2 x N2 |
|
|
... |
M S |
N S |
|
x2 p1 x q1 |
|
x2 p x q |
2 |
x2 p x q |
S |
|||
|
|
|||||||
|
1 |
1 |
|
1 |
1 |
|||
37

|
P x Q |
|
P x |
Q |
|
|
|
|
P |
Q |
|
|
||
|
1 |
1 |
|
|
2 |
2 |
|
|
... |
|
P |
P |
|
... , |
|
x2 |
p2 x q2 |
x2 |
p |
x q |
2 |
|
|
x2 p |
x q |
P |
|||
|
|
|
|
|
||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
2 |
|
2 |
|
|
где A1, A2 ,..., Qp |
- |
некоторые |
|
действительные числа, |
||||||||||
находящиеся по методу неопределѐнных коэффициентов.
Суть метода неопределенных коэффициентов сводится к тому, что предыдущее равенство приводится к общему знаменателю, после чего тождественно приравниваются числители правой и левой части. Условие тождественности означает равенство коэффициентов при одинаковых степенях x слева и справа, из чего и получается система уравнений относительно искомых чисел A1 , A2 , B1… и т.д.
Число простейших дробей, соответствующих каждому множителю знаменателя, ровно кратности соответствующего корня.
Пример 2.15. Вычислить интеграл |
x |
1 |
dx. |
|
|
||
x(x |
2)2 |
Решение: Подынтегральная функция представляет собой правильную рациональную дробь. Разложим ее на сумму простейших дробей.
|
|
|
|
|
|
|
x |
1 |
|
|
A B |
|
C |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
|
x x 2 2 |
|
|
x x 2 |
x 2 2 |
|||||||||||
|
Приведем правую часть равенства к общему знаменателю |
||||||||||||||||||||
и приравняем числители. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
A |
|
|
B |
|
|
C |
|
|
|
A x 2 2 |
|
Bx x 2 Cx |
|
||||||
|
|
x x |
2 x |
2 2 |
|
|
|
|
|
|
|
x 2 2 x |
|||||||||
|
A B x2 |
2A 2B C x 4A |
, |
|
|
|
|
|
|||||||||||||
|
|
|
|
x |
2 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
A B x2 |
|
2A 2B C x 4A x 1. |
|||||||||||||||
Приравнивая одинаковые коэффициенты, получим систему уравнений:
38
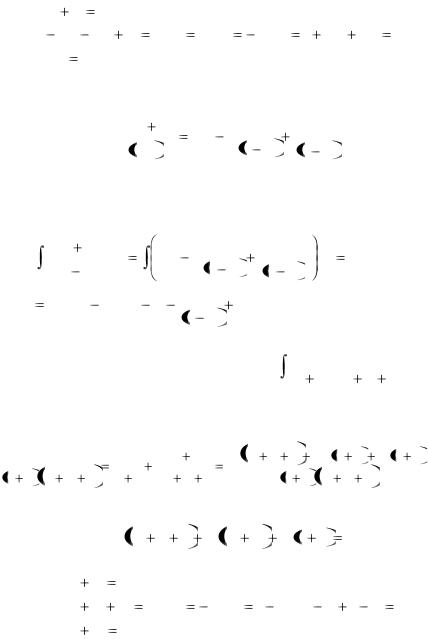
|
x 2 |
|
A |
B |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x1 |
|
|
|
|
2 A 2B C 1 |
A |
|
, B |
, C 1 2 A 2B 1 . |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
4 |
|
|||||||||||||||||||||||||||||||||||||
|
x0 |
|
4 A 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Подставим найденные коэффициенты в разложение |
||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||
рациональной функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
1 |
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x-2 2 x |
|
4x 4 x 2 |
x 2 2 |
|
|
|
|||||||||||||||||||||
|
|
Искомый интеграл представляется в виде суммы |
||||||||||||||||||||||||||||||||||||||||||
интегралов от простейших дробей: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x 1 |
|
|
|
dx |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
dx |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
x(x 2)2 |
|
|
|
4x 4 x 2 |
|
x 2 2 |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
ln |
|
x |
|
|
|
|
|
|
1 |
|
|
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
ln |
x |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
4 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
1 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Пример 2.16. Вычислить интеграл |
|
|
|
|
dx . |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1)(x2 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
x 1) |
|
||||
|
|
Решение: Разложим правильную рациональную дробь на |
||||||||||||||||||||||||||||||||||||||||||
простейшие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
Bx C |
|
|
A x2 |
|
|
x 1 Bx x 1 C x 1 |
. |
||||||||||||||||||||
|
x 1 x2 |
x 1 x 1 |
|
x2 |
x 1 |
|
|
|
|
|
|
|
x 1 x2 x 1 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
Приравняем числители: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A x2 |
|
|
x 1 B x2 x C x 1 1. |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x 2 |
|
A |
B |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x1 |
|
A B C 0 |
B A, C 1 A, A A 1 A 0, . |
|
||||||||||||||||||||||||||||||||||||||
|
|
x0 |
|
A |
C |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39
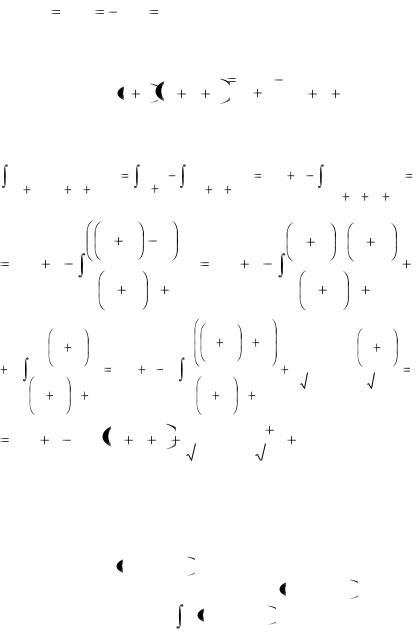
|
|
|
|
|
A |
|
|
|
1, B |
|
|
|
1, C |
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
Подставим найденные коэффициенты в разложение |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
рациональной функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 x2 |
|
|
|
|
x 1 |
|
|
|
|
|
|
x 1 |
x2 |
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Окончательно получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
dx |
|
|
|
|
ln |
|
x |
1 |
|
|
|
|
|
|
|
|
|
xdx |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
||||||||||||||||||||||||||||||
|
(x 1)(x |
x |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
1 |
|
|
|
|
1 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
d |
x |
|
|
|
1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
ln |
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
1 |
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
2 |
3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
x |
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||
|
|
|
|
|
d |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
x |
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
x |
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
3 |
|
3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
ln x2 |
|
|
|
|
|
|
|
|
|
1 |
|
arctg |
2x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
ln |
x |
1 |
|
|
|
|
|
x |
|
1 |
|
|
|
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2. 9. Интегрирование тригонометрических выражений |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Рассмотрим случаи интегрирования тригонометрических |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
функций. |
Рациональную функцию переменных sin x |
и cos x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
обозначим |
|
|
R sin x, cos x . |
|
|
|
|
|
Пусть |
|
надо |
|
|
вычислить |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
неопределенный интеграл от функции R sin x, cos x : |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
R cos x, sin x dx .
40
