
2777
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
z1 z2 |
2 2 cos |
|
|
|
i sin |
|
|
|
2 2 cos |
|
|
i sin |
|
|
|||||
|
6 |
|
6 |
|
|
||||||||||||||
|
4 |
4 |
12 |
|
12 |
||||||||||||||
Деление комплексных чисел определяется как операция,
обратная операции умножения. Частным от деления двух комплексных чисел z1 и z2 0 называется комплексное число z , которое, будучи умноженным на z2 , дает число z1 , т.е.
z1 |
z , если z z2 |
z1 . |
|
z2 |
|||
|
|
Практически деление комплексных чисел в алгебраическом представлении производится посредством умножения числителя и знаменателя на число, комплексно сопряженное знаменателю:
z1 |
|
x1 |
iy1 |
|
|
x1 |
iy1 x2 |
iy2 |
|
|
x1x2 |
y1 y2 |
|
i y1x2 x1 y2 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
x2 |
iy2 |
|
|
x2 |
iy2 x2 |
iy2 |
|
|
|
x22 |
|
y22 |
||||||||||
|
|
Пример 1.6. Выполнить деление |
1 |
|
i |
. |
|
|
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3i |
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 i |
|
|
1 i 2 3i |
|
2 3i 2i |
3 |
|
|
|
1 |
|
5i |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 3i |
|
2 3i 2 3i |
4 9 |
|
|
|
|
13 13 |
|
||||||||||||
|
|
При |
делении |
комплексных |
чисел |
z1 |
и z2, заданных в |
|||||||||||||||||
тригонометрической форме, модули комплексных чисел делятся, а аргументы вычитаются. По определению:
z |
zz |
2 |
|
z |
|
z |
|
z |
2 |
|
z |
|
|
|
z1 |
|
, |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
z2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Arg z1 Arg z |
|
Arg z2 |
|
Arg z |
Arg z1 |
|
Arg z2 . |
||||||||||
Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя.
z1 |
|
r1 |
cos |
|
|
i sin |
|
|
. |
z2 |
|
r2 |
1 |
2 |
1 |
2 |
|||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
11

В показательном представлении операции с модулями и аргументами комплексных чисел при делении совпадают с таковыми при делении в тригонометрическом виде:
z1 |
|
r1 |
ei 1 2 . |
z2 |
|
r2 |
|
|
|
Возведение комплексного числа в целую положительную степень является распространением правила умножения комплексных чисел на случай, когда все n множителей одинаковы. В алгебраическом представлении возведение комплексного числа в n -ую степень производится по алгебраическим правилам перемножения многочленов с учетом того, что
i2 |
1, i3 |
i2i |
i, i4 |
i3i 1. |
В тригонометрическом представлении модуль n -ой степени комплексного числа равен n - ой степени модуля исходного комплексного числа, а аргумент n -ой степени комплексного числа получается посредством умножения на n аргумента исходного комплексного числа. В итоге получается
формула Муавра:
|
|
|
|
|
|
z n |
r n cosn |
|
|
i sin n . |
|
|
|
|
|||||||||
|
В показательном представлении имеем: |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
z n |
|
|
|
|
|
r n ein . |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
i 12 . |
|
|
|
|
|
|
|||||
|
Пример 1.7. Вычислить ( |
3 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение: |
Запишем |
|
|
|
|
|
|
число |
|
z |
|
3 i |
в |
|||||||||
тригонометрическом |
виде, |
|
|
|
|
|
учтя |
при |
этом, |
что |
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r |
3 |
|
2 , |
arctg |
|
|
|
|
, |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
z |
2 cos |
|
|
i sin |
|
. |
|
|
|
|
|||||||
|
|
|
|
|
|
6 |
|
6 |
|
|
|
|
|||||||||||
Произведя по указанным правилам возведение в двенадцатую степень комплексного числа, имеем
12
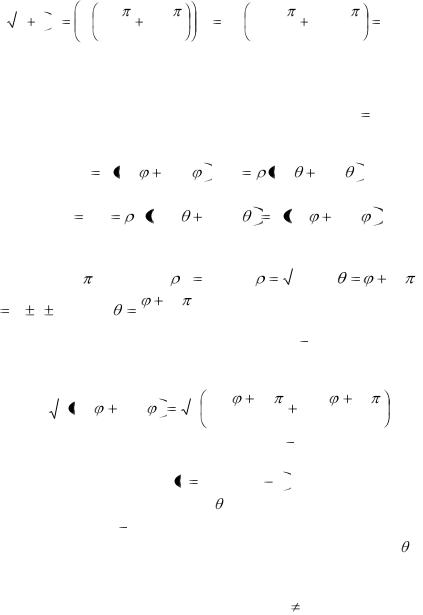
|
|
|
|
|
|
|
12 |
12 |
|
12 |
|
|
|
|
|
|
|
212 cos |
|
212. |
|||||
( |
3 |
i 12 |
2 cos |
|
i sin |
|
i sin |
|||||
|
|
|
|
|
||||||||
|
|
|
6 |
6 |
6 |
|
6 |
|
||||
Извлечение корня n - степени определяется как действие, обратное возведению в натуральную степень. Корнем n-ой степени из комплексного числа z называется такое
комплексное число w , что выполняется равенство wn |
z . |
||||||
Если комплексные |
числа z |
и w представлены в |
|||||
тригонометрической форме |
|
|
|
|
|||
z |
r cos |
i sin |
и w |
cos |
i sin |
, |
|
то, по определению корня и формуле Муавра, получаем |
|||||||
z |
wn |
n cosn |
i sin n |
r cos |
i sin . |
||
Согласно определению два комплексных числа равны, если равны их модули, а аргументы равны или отличаются на
|
|
n r |
|
|
|
|
|
|
||
четное число , поэтому |
или |
n r , а n |
2k |
, |
||||||
k 0, |
1, 2,... или |
|
2k |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
В |
результате определению |
корня |
n ой |
степени |
из |
|||||
комплексного числа удовлетворяю n комплексных чисел, описываемых формулой
|
|
|
|
|
|
|
|
2k |
|
|
2k |
|
|
||
n r cos |
i sin |
|
n r |
cos |
i sin |
|
. |
|
|||||||
|
|
|
|
|
|
|
|||||||||
|
n |
|
n |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Операция |
извлечения |
корней n |
ой |
степени |
|
из |
|||||||||
комплексного числа оказывается многозначной, т.е. |
|
n |
|||||||||||||
значениям |
параметра |
k |
k |
0,1,2,..., n 1 |
соответствуют |
n |
|||||||||
различных значений аргумента k , а поэтому и |
n значений |
||||||||||||||
самого корня |
n ой |
|
степени из комплексного числа. |
||||||||||||
Остальным |
целым |
k |
соответствуют |
значения |
|
k , |
|||||||||
отличающиеся от одного из указанных значений на величину, кратную 2π и не дающие новых значений корня.
Таким образом, комплексное число z 0 имеет ровно n корней степени n, получаемых из вышеприведенной формулы. Следует отметить, что все значения корня лежат на
13

окружности радиуса ρ= n r и делят окружность на n равных частей.
r и делят окружность на n равных частей.
|
|
|
4 |
|
|
|||
Пример 1.8. Вычислить |
16 . |
|||||||
Решение: |
Запишем число |
z |
|
16 в тригонометрической |
||||
|
r |
16 , |
|
|
|
|
||
форме: |
z |
, |
|
z |
16 cos i sin . Поэтому |
|||
|
|
|
|
|
|
|
|
|
4 16
16
При
При
При
При
2 , |
|
2k |
. |
|
k |
|
|||
4 |
||||
|
|
|||
|
|
|
k 0 имеем
0 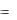 4 , w0
4 , w0
k 1имеем
|
3 |
, w1 |
|
1 |
|
||
4 |
|||
|
|
k 2 имеем
|
5 |
, w2 |
|
2 |
|
||
4 |
|||
|
|
k 3 имеем
|
7 |
, w3 |
|
3 |
|
||
4 |
|||
|
|
2 cos |
|
|
|
|
|
i sin |
|
|
|
|
|
|
|
|
||||||||
4 |
4 |
|
|
|
||||||||||||||||||
2 cos |
3 |
|
|
|
|
|
i sin |
3 |
|
|
|
|
|
|
||||||||
4 |
|
4 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 cos |
|
5 |
|
|
|
|
i sin |
|
5 |
|
|
|
|
|
|
|||||||
4 |
|
4 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 cos |
7 |
|
|
i sin |
7 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
4 |
|
|
|
|
|
4 |
|
|
|
|||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
w1 3 |
|
|
|
|
w0 |
|
|
|
||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
2 |
|||||
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
3 |
|
|
4 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
w2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
w3 |
||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|||||||||||
Рис. 3

 2 i
2 i
 2 .
2 .

 2 i
2 i
 2 .
2 .

 2 i
2 i
 2 .
2 .

 2 i
2 i
 2 .
2 .
x
Вопросы для самопроверки
14
1.Дайте определение комплексного числа.
2.Где на комплексной плоскости изображаются мнимые
числа?
3.Что собой представляет алгебраическая форма записи комплексного числа?
4.Какие комплексные числа называются равными?
5.Относительно какой оси комплексно-сопряженные числа располагаются симметричным образом?
6.Как называется длина радиус-вектора, соответствующего комплексному числу?
7.Что является аргументом комплексного числа?
8.Где находится главное значение аргумента комплексного числа?
9.Как вычисляется аргумент комплексного числа, представленного в алгебраическом виде, расположенного в третьей четверти?
10.Как производится сложение комплексных чисел в алгебраическом представлении?
11.Какими свойствами обладает операция сложения комплексных чисел?
12.Что происходит с аргументами и модулями комплексных чисел при сложении?
13.Дайте определение натуральной степени комплексного числа.
14.Как определяется модуль корня n  степени комплексного числа?
степени комплексного числа?
15.Почему аргумент корня n  степени комплексного числа является многозначным?
степени комплексного числа является многозначным?
15
|
|
|
|
|
|
|
|
|
Задачи для самостоятельного решения |
||||||||||||||||||||||||||||||||||
Произвести действия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
1. |
2 |
|
|
|
|
i |
2 |
i |
|
(Ответ: |
4 |
|
|
|
i |
3 |
). |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
3i |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||||||||
2. |
|
|
|
|
|
|
|
|
|
1 |
|
i |
|
|
|
|
(Ответ: |
1 |
|
|
|
|
|
i |
1 |
). |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
3 |
|
|
i 1 |
|
3i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
3. |
1 |
|
|
|
i 6 (Ответ: |
8i ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
(Ответ: cos |
k |
|
|
|
i sin |
k |
|
|
|
|
|
|
|
||||||||||||||||||||||||
4. |
6 1 |
|
|
|
|
k 0,1,2,3,4,5 |
). |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i, |
i |
3 |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5. |
3 i |
(Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Представить в тригонометрической форме комплексные |
|||||||||||||||||||||||||||||||||||||||||||
числа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1. |
2 |
|
|
|
|
2 3i (Ответ: |
4 cos |
|
|
|
|
|
i sin |
|
). |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
3 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2. |
2 |
|
|
|
|
3 |
|
|
2i |
(Ответ: |
4 cos |
|
|
|
|
|
|
|
|
|
|
i sin |
|
|
). |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
6 |
|
|
|||||||
16
2.НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2.1.Первообразная. Неопределѐнный интеграл
Интегральное исчисление решает задачу нахождения функции F x по известной производной этой функции
F 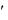 x
x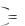 f x .
f x .
|
|
Функция F x |
называется первообразной для функции |
|||||||||||||||
f x |
на |
интервале |
|
a,b , если для |
любого x a,b |
|||||||||||||
выполняется равенство F (x) |
|
|
f (x) или dF x |
f |
x dx . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
||
|
|
Например, |
функция F x |
|
|
|
является первообразной |
|||||||||||
|
|
3 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
для функции f x |
x2 |
на всей числовой прямой, |
так как при |
|||||||||||||||
любом значении аргумента |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|||||
|
|
|
|
|
F |
x |
|
|
|
|
|
x2 |
f |
x . |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Можно заметить, что для функции |
f |
x |
x2 |
существует |
||||||||||||
и |
ряд |
других |
первообразных |
F x |
x3 |
C , |
где |
|||||||||||
3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
C |
произвольная |
|
|
|
постоянная, |
|
|
|
поскольку |
|||||||||
|
x3 |
C |
x2 |
f x |
. |
Это |
указывает |
на |
неоднозначность |
|||||||||
3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
отыскания первообразной F x |
по исходной функции f |
x . |
||||||||||||||||
|
|
Терема 1. |
Если |
F x является первообразной функции |
||||||||||||||
f x |
на |
некотором |
промежутке a,b , |
то |
любая |
другая |
||||||||||||
первообразная для функции |
f |
x на этом промежутке может |
||||||||||||||||
17

быть |
представлена в виде |
F x |
C , |
где |
C |
произвольная |
||||||
постоянная. |
|
|
|
|
|
|
|
|
|
|
||
Доказательство: Поскольку F |
x |
|
f x |
, то |
|
|
||||||
|
|
|
F x |
|
C |
F |
x |
|
f |
x . |
|
|
Является |
ли формула |
F x |
C |
|
исчерпывающей |
при |
||||||
описании |
множества первообразных |
для |
f x |
или могут |
||||||||
существовать |
какие-то |
|
другие |
|
первообразные, |
не |
||||||
содержащиеся в этой формуле? |
|
|
|
|
|
|
|
|||||
Теорема 2: Если две функции F1 |
x |
и F2 |
x являются |
|||||||||
первообразными для f x |
на интервале |
a,b , то их разность |
||||||||||
постоянна для любого x |
(a,b) . |
|
|
|
|
|
|
|
||||
Доказательство: Рассмотрим вспомогательную функцию |
||||||||||||
x |
F1 x |
F2 x . Поскольку |
|
|
|
|
|
|
|
|||
|
x |
F1 x F2 x |
|
F1 x F2 x |
f x f x 0 |
|
||||||
для любого x |
(a,b) , то отсюда следует, что |
|
|
|||||||||
|
|
|
x |
F1 |
x |
F2 |
x |
|
C , |
|
|
|
где C |
const . |
|
|
|
|
|
|
|
|
|
|
|
Важным оказывается вывод о том, что, если производные двух функций тождественно равны, то сами функции могут отличаться лишь на постоянное слагаемое.
Множество всех первообразных функций F x C для
C для
исходной |
функции |
f x |
называется |
неопределенным |
||||
интегралом |
от |
функции |
f x и обозначается |
символом |
||||
f x dx . Здесь |
f x |
называется подынтегральной функцией, |
||||||
f x dx подынтегральным |
выражением, |
x |
переменной |
|||||
|
|
|
|
|
|
|
|
|
интегрирования, 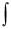 знаком неопределенного интеграла.
знаком неопределенного интеграла.
Таким образом, по определению
 f x dx F x
f x dx F x C .
C .
18
Неопределенный интеграл обозначает совокупность всех первообразных для функции f x , однако иногда он может обозначать какую-то из первообразных.
Операция нахождения неопределенного интеграла от
функции f |
x |
называется |
интегрированием этой |
функции. |
||||
Геометрически |
неопределенный |
интеграл |
соответствует |
|||||
множеству |
кривых y |
F x |
C , |
каждая |
из |
которых |
||
называется интегральной кривой. |
|
|
|
|
||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
y |
F x |
C3 |
|
|
|
|
|
|
y |
F x |
C2 |
|
|
O |
|
|
x |
|
|
|
|
|
|
|
y |
F x |
C1 |
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
y |
F x |
|
|
|
|
Рис. 4 |
|
|
|
|
|
|
Функция, |
имеющая |
первообразную, |
называется |
|||||
интегрируемой. Имеет место теорема, которая утверждает, что для всякой непрерывной на интервале a,b функции
существует первообразная на (a, b), т.е. непрерывная функция интегрируема.
Интегрирование представляет собой операцию, обратную
дифференцированию. |
Правильность |
выполнения |
|
интегрирования |
достаточно |
легко |
проверить, |
продифференцировав результат, и получить при этом подынтегральную функцию. Например,
x5 dx |
|
x6 |
|
|
x6 |
C |
|
x5 , |
|
|
|
|
|||||||
|
|
|
|
C, |
так как |
|
|
ctgxdx ln |
sin x |
C, |
|||||||||
6 |
6 |
|
|||||||||||||||||
|
|
|
|
|
|
8x |
|
|
1 |
|
8x |
|
|
|
|||||
так как |
ln |
|
sin x |
|
C |
ctgx , |
e |
dx |
e |
C, так как |
|||||||||
|
|
||||||||||||||||||
|
|
|
8 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
19
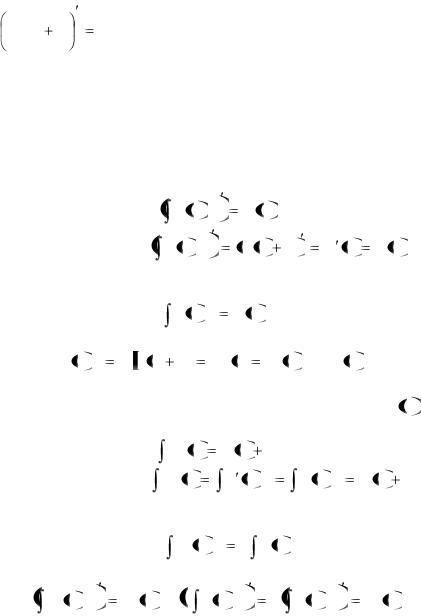
1 |
e |
8x |
C |
e |
8x |
. |
8 |
|
|
||||
|
|
|
|
|
|
2.2. Основные свойства неопределѐнного интеграла
Основные свойства неопределенного интеграла вытекают непосредственно из его определения.
1. Производная от неопределѐнного интеграла равна подынтегральной функции:
|
f |
x dx |
f x . |
|
Действительно, |
f |
x dx |
F x C |
F x f x . |
2. Дифференциал от неопределѐнного интеграла равен |
||||
подынтегральному выражению: |
|
|
||
d |
f |
x dx |
f x dx . |
|
Действительно,
d  f x dx d F x
f x dx d F x C
C dF x
dF x F
F  x dx
x dx 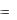 f x dx .
f x dx .
3. Неопределенный интеграл от дифференциала некоторой функции равен сумме данной функции F x и произвольной постоянной:
|
|
dF x |
F x |
C . |
|
|
|
|
||
Действительно: |
dF x |
|
F |
x dx |
f |
x dx |
F x |
C . |
||
4. Постоянный множитель можно выносить за знак |
||||||||||
неопределѐнного интеграла: |
|
|
|
|
|
|
|
|
||
|
|
af |
x dx |
a |
f x dx . |
|
|
|
||
Действительно: |
|
|
|
|
|
|
|
|
|
|
af x dx |
af x |
и a |
f |
x dx |
a |
f |
x dx |
af |
x . |
|
Если производные двух величин одинаковы, то сами величины могут отличаться только на постоянную. Поскольку неопределенные интегралы определены с точностью до
20
