
2777
.pdf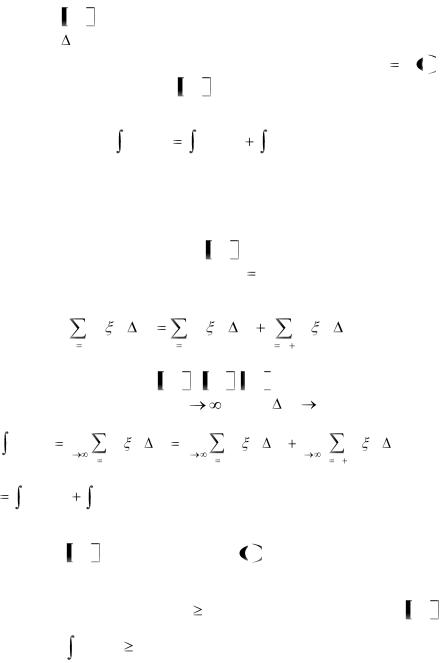
отрезка |
a, b |
от b |
к a |
в интегральной сумме меняется знак |
|
каждого |
xk |
на противоположный. |
|
||
4. |
Свойство |
аддитивности: |
Если функция y f x |
||
интегрируема на отрезке |
a, b и a<c<b, то |
||||
|
|
b |
|
c |
b |
|
|
f (x)dx |
f (x)dx |
f (x)dx , |
|
|
|
a |
|
a |
c |
т.е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка.
Доказательство:
При разбиении отрезка a, b на части точка с включается в число точек деления, т.е. xm c . Интегральная сумма разбивается на две суммы:
|
n |
|
|
m |
|
|
n |
|
|
|
|
|
|
|
f ( k ) xk |
|
|
f ( k ) xk |
|
f ( k ) xk . |
|
||||
|
k 1 |
|
|
k |
1 |
|
k m 1 |
|
|
|
||
Каждая из указанных сумм является интегральной |
||||||||||||
суммой для отрезков |
a, b , |
a, c , c,b . Перейдем к пределу в |
||||||||||
последнем равенстве при n |
|
и max |
xk |
|
0 : |
|
||||||
b |
|
n |
|
|
|
m |
|
|
|
|
n |
|
f (x)dx |
lim |
f ( |
k ) |
xk |
lim |
f ( k ) |
xk |
lim |
|
f ( k ) xk = |
||
a |
n |
k 1 |
|
|
m |
k 1 |
|
|
n |
k |
m 1 |
|
|
|
|
|
|
|
|
|
|||||
c |
b |
|
|
|
|
|
|
|
|
|
|
|
f (x)dx |
f (x)dx . |
|
|
|
|
|
|
|
|
|
||
a |
c |
|
|
|
|
|
|
|
|
|
|
|
Свойство 4 справедливо при расположении точки c |
вне |
|||||||||||
отрезка |
a, b , если |
функция |
f x |
продолжает оставаться |
||||||||
интегрируемой на каждом из получающихся отрезков. |
|
|||||||||||
5. Если функция |
f (x) |
0 интегрируема на отрезке |
a, b |
|||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
(a<b), то |
f (x)dx |
0 . |
|
|
|
|
|
|
|
|
|
|
a
61
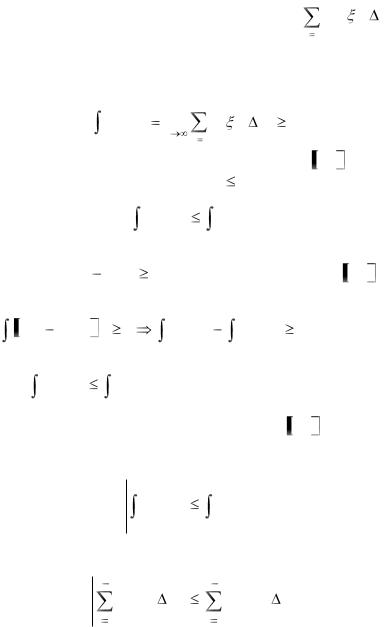
Доказательство:
n |
|
Каждое слагаемое интегральной суммы |
Af ( k ) xk |
k |
1 |
неотрицательно, поэтому интегральная сумма тоже является неотрицательной. Предел неотрицательной величины не может быть отрицательным, поэтому
|
|
b |
|
n |
|
|
|
|
|
|
f (x)dx |
lim |
f ( |
k ) xk |
0 . |
|
|
|
|
a |
n |
k 1 |
|
|
|
|
|
|
|
|
|
|
|
||
6. Если f(x) и g(x) интегрируемы на отрезке |
a, b |
(a<b) и |
||||||
удовлетворяют на нѐм равенству |
f (x) |
g(x) , то |
|
|
||||
|
|
b |
|
b |
|
|
|
|
|
|
f (x)dx |
g(x)dx . |
|
|
|
||
|
|
a |
|
a |
|
|
|
|
Доказательство: |
|
|
|
|
|
|
||
Так как g(x) |
f (x) 0 |
для всех |
x из отрезка |
a, b , то |
||||
по свойству 5: |
|
|
|
|
|
|
|
|
b |
|
b |
|
b |
|
|
|
|
g(x) |
f (x) dx 0 |
g(x)dx |
f (x)dx 0 |
|
|
|||
a |
|
a |
|
a |
|
|
|
|
b |
|
b |
|
|
|
|
|
|
или f ( x)dx |
g( x)dx . |
|
|
|
|
|
|
|
a |
|
a |
|
|
|
|
|
|
7. Если |
f(x) |
интегрируема |
на отрезке |
a, b |
и |
a<b, то |
||
модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции, т.е.
b |
b |
|||
f (x)dx |
|
f (x) |
|
dx . |
|
|
|||
a |
a |
|||
Доказательство: Поскольку модуль суммы слагаемых не превосходит сумму модулей этих слагаемых, то
n 1 |
n 1 |
||
f ( xk ) xk |
|
f ( xk ) |
xk . |
k 0 |
k 0 |
||
62
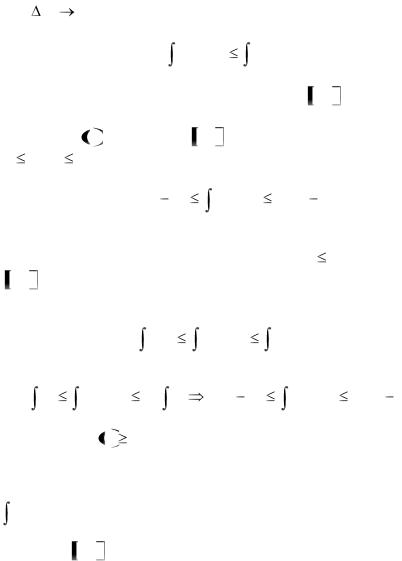
|
Переходя в |
обеих частях неравенства к пределу при |
||||||
max |
xk 0 , получим формулу |
|
|
|
|
|||
|
|
|
b |
|
b |
|||
|
|
|
|
|||||
|
|
|
f (x)dx |
|
|
f (x) |
|
dx . |
|
|
|
|
|
|
|||
|
|
|
a |
|
a |
|||
|
8. Если функция f(x) интегрируема на a, b (a<b) и числа |
|||||||
m и |
М являются |
наименьшим |
и наибольшим значениями |
|||||
функции |
f x на отрезке |
a, b , т.е. выполняется неравенство |
m f (x) |
M , то |
|
|
|
b |
|
m(b a) |
f ( x)dx M (b a) . |
a
Доказательство:
Проинтегрируем неравенство m 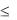 f (x) M по отрезку a, b . При интегрировании воспользуемся свойством 6. В результате получим:
f (x) M по отрезку a, b . При интегрировании воспользуемся свойством 6. В результате получим:
|
b |
|
b |
b |
|
|
|
mdx |
f (x)dx |
|
Mdx или |
|
a |
|
a |
a |
|
b |
b |
b |
|
|
b |
m dx |
f ( x)dx M dx m(b a) |
f ( x)dx M (b a) . |
|||
a |
a |
a |
|
|
a |
Если |
f x 0 , |
то |
свойство |
8 |
допускает наглядную |
геометрическую интерпретацию: площадь криволинейной трапеции, соответствующей определенному интегралу
b
f (x)dx , заключена между площадями прямоугольников с
a
отрезком a, b в основании и высотами, равными m и M , как показано на рисунке 6.
63

y
y 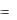 f x
f x
M
m
O a |
b x |
Рис.6.
Данное свойство используется для оценки определенного интеграла.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
dx |
|
|
|||
Пример 3.1. Оценить интеграл: I |
|
|
. |
|
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 1 tgx |
|
|||||
Решение: |
Поскольку |
на |
отрезке |
|
|
0, |
|
|
|
выполняется |
||||||||||
|
|
4 |
|
|
||||||||||||||||
неравенство |
1 |
|
1 |
|
1, то |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
1 tgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
dx |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
8 |
0 1 |
tgx |
4 |
|
|
|
|
|
|||||||
9. Теорема о среднем для определѐнного интеграла. |
||||||||||||||||||||
Теорема: |
Если |
функция |
f x непрерывна на отрезке |
|||||||||||||||||
a, b , то внутри отрезка найдется хотя бы одна точка c такая, что
b
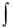 f (x)dx
f (x)dx 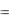 f (c)(b a) .
f (c)(b a) .
a
Доказательство: Полагаем, что a<b. Так как функция непрерывна на отрезке a, b , то она достигает на нѐм своего наибольшего М и наименьшего m значений: m 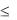 f (x) M .
f (x) M .
64

Проинтегрировав это неравенство в пределах от а до b, получим:
b
m(b a) 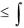 f ( x)dx M (b a) .
f ( x)dx M (b a) .
a
После деления на (b-a)>0 имеем:
|
|
1 |
|
b |
m |
|
|
f (x)dx M |
|
|
|
|
||
|
|
|
||
|
b |
|
a a |
|
Так как функция f(x) непрерывна на отрезке a, b , то она принимает любое промежуточное значение, заключѐнное
|
|
|
|
|
1 |
b |
|
|
|
между m и M . |
Поэтому |
|
f (x)dx - |
одно из значений |
|||||
|
|
||||||||
b a a |
|||||||||
|
|
|
|
|
|
|
|||
функции f(x) на |
a,b , т.е. |
|
|
|
|
||||
|
|
1 |
|
b |
|
|
b |
|
|
f (c) |
|
|
f ( x)dx или |
f (x)dx |
f (c)(b a) . |
||||
|
|
|
|||||||
|
|
|
|||||||
|
b |
|
a a |
|
|
a |
|
||
Геометрический смысл теоремы о среднем состоит в том, что криволинейная трапеция, соответствующая определенному
b
интегралу f (x)dx , равновелика прямоугольнику с длиной
a
основания (b-a) и высотой f(c).
3.5. Определѐнный интеграл с переменными верхним пределом.
Пусть неотрицательная функция |
f(x) интегрируема на |
|
|
b |
|
отрезке a, b . Тогда |
f (x)dx S |
представляет число, |
a
соответствующее площади криволинейной трапеции. Если верхний предел интегрирования b будет менять свое
65

положение, то, очевидно, будет меняться и площадь изменяющейся криволинейной трапеции, т.е. S S b . В определѐнном интеграле переменную интегрирования можно обозначить любым другим символом, например t :
b |
|
b |
|
|
f (x)dx |
f (t)dt S b . |
|
a |
|
a |
|
Рассмотрим отрезок с переменным верхним пределом |
a, x , |
||
|
|
x |
|
где a x b . Тогда |
определенный интеграл f (t)dt |
S x |
|
a
оказывается функцией переменного верхнего предела интегрирования
x
( x) 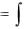 f (t)dt .
f (t)dt .
a
Теорема Барроу: Если функция f x непрерывна на
отрезке |
a, b , то производная от функции (x) равна f x , |
т.е. (x) |
есть первообразная для f(x) на a, b : |
|
(x) f (x) . |
Другими словами: производная от определѐнного интеграла по переменному верхнему пределу равна подынтегральной
функции, |
в |
которой |
аргумент t |
заменяется |
на |
x : |
||||
|
f (x) . |
|
|
|
|
|
|
|||
f (t) |
|
t x |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
Доказательство: |
|
|
|
|
|
|
||
|
|
Для |
нахождения |
производной |
(x) |
назначим |
||||
приращение |
x для верхней |
границы интегрирования |
x и |
|||||||
найдѐм приращение функции |
(x) : |
|
|
|
|
|||||
|
|
|
|
|
|
x |
x |
x |
|
|
|
|
|
(x) |
(x |
x) |
(x) |
f (t)dt |
f (t)dt . |
|
|
|
|
|
|
|
|
a |
|
a |
|
|
Переставляя местами пределы интегрирования во втором интеграле и используя свойство аддитивности 4, получим:
66

|
|
|
|
|
x |
|
x |
|
|
|
|
||
|
|
|
(x) |
|
|
f (t)dt . |
|
|
|
|
|||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
Применяя теорему о среднем к отрезку |
|
x, x |
x , имеем: |
|||||||||
|
|
|
(x) |
f (c) x , |
|
|
|
|
|||||
где |
c является |
некоторой |
внутренней |
точкой |
отрезка |
||||||||
x, x |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная |
|
(x) |
находится |
непосредственным |
||||||||
образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) lim |
(x) |
|
lim |
|
f c x |
|
lim f (c) |
f x , |
||||
|
x |
|
x |
||||||||||
|
x |
0 |
x |
0 |
|
x |
0 |
|
|
||||
поскольку при x 0 c x . Последнее |
соотношение и |
|
является доказательством того, что |
функция |
(x) является |
первообразной для f(x), непрерывной |
на a, b . |
|
Из теоремы Барроу следует, что неопределенный интеграл может быть представлен с использованием определенного интеграла с переменным верхним пределом:
|
|
x |
f (x)dx |
(x) C |
f (t)dt C . |
|
|
a |
3.6. Формула Ньютона-Лейбница |
||
Пусть функция y |
f x интегрируема на отрезке a, b . |
|
Тогда способ вычисления определенных интегралов может быть получен с помощью формулы Ньютона-Лейбница.
67

|
Теорема: |
Если |
функция |
f |
x |
непрерывна |
на |
отрезке |
||
a, b |
и F x есть какая-либо ее первообразная, то имеет место |
|||||||||
формула Ньютона-Лейбница: |
|
|
|
|
|
|
||||
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
f (x)dx F (b) |
F (a) . |
|
|
|
|||
|
|
a |
|
|
|
|
|
|
|
|
|
Доказательство. Согласно теореме Барроу |
|
|
|||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
f (t)dt |
F x |
C , |
|
|
|
||
|
|
|
a |
|
|
|
|
|
|
|
где |
F x является |
первообразной для |
функции |
f x . |
||||||
Постоянную величину C легко определить, положив x |
a : |
|||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
f (t)dt |
0 |
F a |
C или C |
F a . |
|
|
||
|
a |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
Поэтому: |
|
f (t)dt F ( x) |
F (a) . |
Это |
равенство |
||||
|
|
a |
|
|
|
|
|
|
|
|
справедливо для любых |
x |
a,b . |
Положив x b , получим |
|||||||
формулу Ньютона-Лейбница: |
|
|
|
|
|
|
||||
|
b |
|
|
|
|
|
b |
|
|
|
|
f (t)dt F (b) |
F (a) |
или |
f (x)dx |
F (b) |
F (a) . |
||||
|
a |
|
|
|
|
|
a |
|
|
|
|
Формула |
Ньютона-Лейбница |
представляет |
удобный |
||||||
способ вычисления определенного интеграла: сначала находится первообразная, затем вычисляется разность значений первообразной на концах отрезка a, b .
Пример 3.2. Вычислить определенный интеграл |
5e ln x dx |
. |
|||||||||||
e |
|
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
Решение: |
|
|
|
|
|
|
|
|
|
|
|||
5e |
|
|
5e |
|
|
|
|
|
|
|
|
||
ln x dx |
|
ln x |
2 |
5e |
1 |
ln 5e 2 |
ln e 2 |
|
|
||||
|
ln x d ln x |
|
|
|
|
||||||||
|
x |
2 |
|
e 2 |
|
|
|||||||
e |
e |
|
|
|
|
|
|
||||||
|
|
|
|
68 |
|
|
|
|
|
|
|
|
|
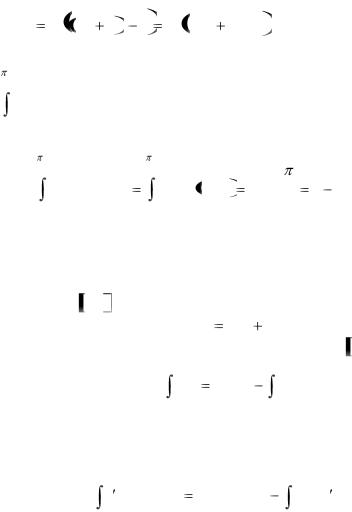
|
|
|
|
1 |
ln 5 1 2 |
1 |
|
1 |
ln2 5 2 ln 5 . |
|
|
|
||
2 |
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||
|
Пример 3.3. |
|
|
Вычислить |
определенный интеграл |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
esin x cos x dx. |
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
esin x cos x dx |
|
|
esin x d sin x |
esin x |
2 |
e 1 . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
0 |
|
|
|
|
0 |
|
||||
3.7. Интегрирование по частям в определѐнном интеграле.
Пусть функции u(x) и v(x) непрерывно дифференцируемы на отрезке a, b . Дифференциал произведения функций равен
d(uv) udv vdu .
Интегрирование этого тождества на отрезке a, b дает
дает
b |
b |
||
udv (uv) |
|
ba |
vdu . |
|
|||
|
|
||
a |
a |
||
Раскрывая дифференциалы, фигурирующие в равенстве, получаем формулу интегрирования по частям в определенном интеграле:
b |
b |
||
v ( x)u( x)dx u( x)v( x) |
|
ba |
v( x)u ( x)dx . |
|
|||
|
|
||
a |
a |
||
Подобно тому, как в неопределенном интеграле выделяются три случая представления подынтегрального выражения в виде произведения u и dv , так же и при интегрировании по частям в определенном интеграле появляются три варианта.
69
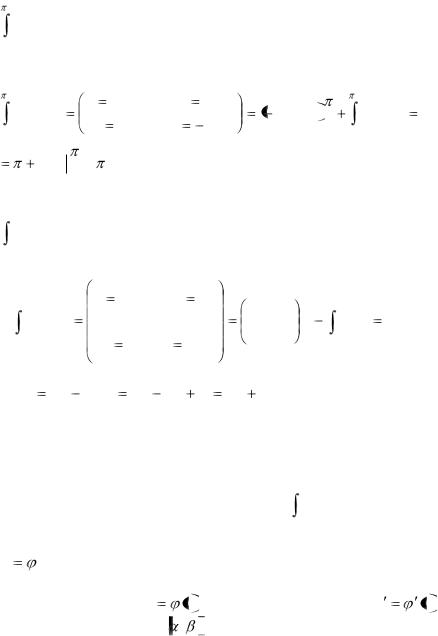
Пример 3.4. Вычислить
x sin xdx.
0
Решение:
|
x sin xdx |
u |
x, |
du |
dx |
|
dv |
sin xdx, |
v |
cos x |
|
0 |
|
||||
|
|
|
|
|
sin x 0 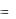 .
.
Пример 3.5. Вычислить
e
x ln xdx.
1
Решение:
|
|
|
u |
|
ln x, |
|
du |
|
dx |
|
|
|||||
e |
|
|
|
|
|
|
|
|
||||||||
|
|
x |
|
|
||||||||||||
x ln xdx |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
x2 |
|
|
||||||
1 |
|
|
dv |
xdx, |
v |
|
|
|||||||||
|
|
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
e2 |
|
x 2 |
e |
|
e2 |
|
|
e2 |
|
|
1 e2 |
||||
|
2 |
|
4 |
1 |
|
2 |
|
|
4 |
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определенный интеграл
x cos x |
|
0 |
cos x dx |
|
0 |
||
|
|
|
определенный интеграл
x2 ln x |
|
e |
e |
x2 dx |
||
2 |
|
1 |
1 |
2x |
||
|
1 |
. |
|
|
|
|
4 |
|
|
|
|
||
|
|
|
|
|
||
3.8. Замена переменной в определѐнном интеграле
|
|
|
|
b |
|
|
|
Пусть |
для вычисления |
интеграла f ( x)dx , |
где |
f(x) – |
|
|
|
|
|
a |
|
|
некоторая |
непрерывная |
функция, требуется сделать |
замену |
|||
x |
(t) . |
|
|
|
|
|
|
Теорема. Если: |
|
|
|
|
|
|
1) функция x |
t |
и ее производная |
x |
t |
|
непрерывны на отрезке |
, |
, |
|
|
||
70
