
2773
.pdf
b |
|
|
|
|
|
f (x)dx |
F (b) F (a) |
- формула Ньютона-Лейбница.(12) |
|||
a |
|
|
|
|
|
Будем |
обозначать |
F (b) F (a) F ( x) |
|
b |
- двойная |
|
|||||
|
|
|
|
a |
|
|
|
|
|
|
|
подстановка.
Пример 1. Вычислить
16).
y
y= x 2
S=7/3
0
12 x
Рис. 16 .
определенный интеграл (рис.
y |
|
|
|
|
|
|
|
|
|
|
y=sinx |
||||||
1 |
|
|
|
|
|
|
|
S=2 |
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x |
|
||
|
|
|
|
|
|
|
|
|
Рис. 17.
2 x2dx |
|
x3 |
|
2 |
8 |
|
1 |
|
|
|
7 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 |
|
1 |
3 |
3 |
|
|
3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Вычислить определенный интеграл (рис. |
|||||||||||||||||
17). sin xdx |
|
|
|
|
|
|
|
|
|||||||||
cos x |
|
0 |
|
|
t |
2 |
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. |
По условию F (x) |
f (x) |
x |
a,b . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
Кроме того, |
по доказанной теореме Φ(x) |
f (t)dt |
также |
||||||||||||||
a
является первообразной. Но разность двух первообразных
71

постоянна: Φ(x) |
F(x) |
C |
или |
Φ(x) |
|
F(x) |
C , |
т.е. |
||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t)dt |
|
|
F (x) |
|
c |
x |
a,b . Найдѐм с. Положим, х=а: |
|
||||||||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Тогда |
|
|
|
f (t)dt |
0 и 0 |
F(a) |
|
c |
c |
|
F(a) . |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Поэтому: |
|
|
|
|
|
|
|
f (t)dt |
|
F ( x) |
|
F (a) . |
Это |
равенство |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
справедливо для любых x |
a,b . Положим x=b: |
|
|
|||||||||||||||||||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
f (t)dt |
|
|
F (b) F (a) |
или |
|
f (x)dx |
F (b) |
F (a) . |
|
||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1. |
|
|
|
|
|
|
|
|
|
|
arctgx |
|
1 |
|
|
arctg1 |
arctg0 |
|
|
. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
0 1 |
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
4 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
3 |
|
dx |
|
|
1 |
|
3 |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2. |
|
|
|
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x |
2 |
|
|
|
|
|
x |
|
1 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
dx |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3. |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
2 . |
Получили абсурд, |
так |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
x2 |
|
|
|
|
x |
|
|
1 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
как |
1 |
|
|
терпит |
|
разрыв |
в |
точке |
х=0 |
применять |
формулу |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
x2 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ньютона-Лейбница нельзя.
72

3.6. Интегрирование по частям в определѐнном интеграле
Пусть функции u(x) и v(x) непрерывно дифференцируемы в a, b . Тогда, дифференцируя произведение получим
du(x)v(x) udv vdu.
Проинтегрируем |
это |
тождество |
по |
х |
в |
||||
промежутке a, b . |
|
|
|
|
|
|
|
||
b |
b |
|
|
|
|
||||
udv uv |
|
b |
|
|
vdu . |
|
|
|
|
|
|
|
|
|
|
||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
|
|
|
|
||||
Эту формулу надо понимать так: |
|
|
|
||||||
b |
|
|
|
b |
|
|
|
||
v (x)u(x)dx u(x)v(x) |
|
b |
v(x)u (x)dx . |
|
|
|
|||
|
|
|
|
||||||
a |
|
|
a |
a |
|
|
|
||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
Формула такая же, интеграла, но в результат интегрирования.
1
Пример. ln(1 x)dx
0 |
|
|
|
|
|
|
|
1 |
xdx |
x ln(1 x) |
|
10 |
|
|
|
||||
|
|
x 1 |
||
|
|
|||
|
|
|
|
|
|
|
|
0 |
|
что и для неопределѐнного надо подставить пределы
u |
ln(1 |
x); du |
|
dx |
; |
|||
|
|
|||||||
|
|
|
|
1 |
x |
|
||
dv |
dx; |
|
v |
x. |
|
|
||
|
1 |
1 |
dx |
|
|
|||
ln 2 |
dx |
|
|
|
||||
|
|
|
|
|
|
|
||
|
x |
1 |
|
|
|
|||
|
|
|
|
|
|
|||
|
0 |
0 |
|
|
|
|
|
|
ln 2 x |
|
10 |
ln 2 x |
|
10 ln(1 x) |
|
10 ln 2 1 ln 2 |
|
|
|
|||||
|
|
|
|
||||
2 ln 2 |
|
|
1. |
|
|
|
|
73

3.7. Замена переменной в определѐнном интеграле b
Пусть надо вычислить f (x)dx , где f(x) – некоторая
a
непрерывная функция.
Часто для нахождения первообразной приходится вводить новую переменную x 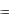 (t) . При этом пользуются
(t) . При этом пользуются
следующим правилом:
Теорема. Пусть выполнены следующие условия:
1. |
Функция f(x) непрерывна на отрезке a, b . |
2. |
Функции (t) и (t) непрерывны в промежутке |
, |
и |
a |
(t) |
b |
при |
t |
и |
( ) |
a; ( ) |
b . |
|
|
|
|
|
3. Сложная функция |
f |
(t) |
непрерывна на |
, . |
|||
Тогда |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
f (x)dx |
f |
(t) |
(t)dt |
|
(13) |
|
a
Пояснения.
1. Условия (1) и (2) обеспечивают непрерывность подынтегральных функций в левой и правой частях
формулы (13). Монотонность |
(t) требуется для |
|||
существования обратной функции. |
|
|||
|
x |
|
||
|
b |
|
|
|
|
|
x= (t) |
f(c) |
|
x |
||||
|
||||
a |
|
|
0 |
t |
t |
|
Рис. 18. |
|
74

2. Условие (3) устанавливает соответствие между пределами интегрирования до и после замены переменной по формуле x  (t) .
(t) .
Доказательство. |
|
|
|
|
|
Пусть F(x) является |
первообразной |
для f(x). По |
|||
|
|
|
b |
|
|
формуле Ньютона-Лейбница |
f (x)dx |
F (b) |
F (a). Тогда |
||
|
|
|
a |
|
|
f (t) |
(t)dt |
f (t) d (t) |
F (t) |
|
|
|
|||||
F ( ) |
F ( ) |
F (b) F (a) |
|
|
|
(форма первообразной не зависит от выбора аргумента интегрирования. Раз правые части этих равенств равны, то равны и левые части, что и доказывает формулу (13)).
Замечание. При вычисление неопределѐнного интеграла с помощью замены переменной в найденной первообразной Φ(t) приходилось возвращаться к старой
переменной х. Если в определѐнном интеграле наряду с переменной интегрирования заменить и пределы, то надобность возвращения к исходной переменной отпадает.
Примеры.
1.
|
|
|
|
|
|
|
|
t 2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
x |
t; x |
2 |
|
|
2 |
|
|
|
|
dx |
|
|
|
|
|
2tdt |
|
t 1 1 |
|
||||
|
|
|
dx |
2tdt |
|
|
2 |
|
dt |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
x |
|
x1 |
0;t1 |
0 |
1 t |
|
0 |
t 1 |
||||
0 |
|
|
|
|
x2 |
4;t2 |
2 |
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
75

2 |
|
|
|
2 |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 dt |
|
|
2t |
|
2 |
2 ln |
|
1 t |
|
2 |
|
|
4 2 ln 3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
t 1 |
|
0 |
|
|
0 |
|
|
||||||||||||||||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
x |
|
a sin t |
dx |
a costdt |
|
|
|
|
|||||||||||||||||||
|
|
a 2 |
x2 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
0 t1 |
0 x2 |
|
|
|
a;t2 |
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
a 2 |
a 2 sin2 ta costdt |
|
|
a 2 |
cos2 tdt |
|
|
|
|
|||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
|
1 |
cos2t |
|
|
|
|
a |
|
sin 2t |
|
2 |
|
a |
|
|
|
|||||||||||||||||
a 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
dt |
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
2 |
2 |
2 |
|
|
|
0 |
4 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3.
ln 2 |
|
|
|
|
|
|
|
|
|
e x |
1 |
|
t; x |
ln(t 2 |
1) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2t |
|
|
|
|
|
|
|
|
|
||
|
|
e x 1dx |
|
dx |
|
|
|
dt; |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
1 |
t 2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x1 |
0 t1 0; x2 |
|
|
ln 2 t2 |
1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
|
2t |
|
|
|
1 |
|
t 2 |
1 |
|
1 |
|
|
|
|
|
|
|
|||
|
t |
|
dt |
2 |
|
|
|
dt |
|
|
|
|
|
|
|||||||||
|
|
t 2 |
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|||||||||
0 |
1 |
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
1 |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
dt |
|
|
|
|
|
|
|
2 t |
|
arctgt |
|
10 |
2 1 |
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 1 |
t |
2 |
|
|
|
|
|
4 |
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
76

3.8. Несобственные интегралы
b
При |
определении |
интеграла |
f (x)dx |
a
предполагалось, что :
1.промежуток a, b конечен.
2.функция f(x) определена и непрерывна в a, b
(интегрируемость в смысле Коши)
Рассмотрим теперь интегралы, для которых эти условия нарушаются.
1. Интегралы с бесконечными пределами интегрирования (несобственные интегралы I рода).
Пусть функция f(x) непрерывна в промежутке a,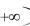 .
.
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На |
данном |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
промежутке |
не |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
существует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определѐнный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интеграл, поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нельзя |
разбить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
промежуток |
a, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|||
|
a |
|
|
|
|
|
N |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на n частей конечной длины.
Рис. 19.
Тем не менее интегралы с бесконечными пределами встречаются как в математике, так и в приложениях. Однако это уже иные интегралы.
Рассмотрим f(x) на a, N (рис. 19). Она интегрируема на этом отрезке:
77

N
(N ) f (x)dx .
a
(14)
Определение. Несобственным интегралом от
функции f(x) по бесконечному |
промежутку a x |
||
называют предел интеграла (14) при N |
: |
||
|
|
N |
|
f (x)dx |
lim |
f (x)dx . |
|
|
N |
|
|
a |
|
a |
|
Если предел существует, то несобственный интеграл называется сходящимся. Если предел не существует или бесконечен, то несобственный интеграл называется расходящимся.
Примеры.
|
|
dx |
|
N |
|
|
dx |
|
|
|
|
|
|
|
|
|
1. |
|
|
lim |
|
|
|
|
|
lim |
arctgx |
|
N |
||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
0 1 |
x |
2 |
N |
1 |
x |
2 |
|
|
N |
|
|
0 |
||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
||||||
Nlim arctgN arctg0 |
|
|
|
. |
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|||||||||||
Интеграл сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
sin xdx |
lim |
sin xdx |
|
|
lim |
cos x |
|
0N |
lim 1 cos N |
|||||||
|
|
|
||||||||||||||
0 |
N |
|
0 |
|
|
N |
|
|
|
|
|
|
N |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Предел не существует – интеграл расходится.
3.dxp . При каких р интеграл сходится и при каких
1 x
расходится?
1) Пусть p>1.
78

|
|
dx |
|
|
|
|
x |
p dx |
|
|
lim |
|
x p |
|
1 |
|
N |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
x p |
|
|
|
|
|
|
|
|
p |
1 |
|
|
|
|
|
|||||||||||||||||||
1 |
1 |
|
|
|
|
|
|
N |
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
lim |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
( p 1)N p 1 |
|
p 1 |
|
|
p 1 |
|||||||||||||||||||||||||||||
N |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Интеграл сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2) Пусть p<1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
dx |
|
|
|
|
x |
p dx |
|
|
x |
p |
1 |
|
|
|
|
|
|
|
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
x p |
0 |
|
|
|
|
p |
1 |
1 |
|
|
|
|
|
|
1 p |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Интеграл расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
3) р=1 |
dx |
ln x |
|
1 |
|
|
|
|
. |
|
|
Интеграл расходится. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P<1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P=1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P>1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 20. |
|
|
|
|
|
|
|
|
|
|
|||||||||
Все три кривые |
y |
1 |
(p>1, p=1, p<1) имеют своей |
||||||||||||||||||||||||||||||||
x p |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
горизонтальной асимптотой ось Ох (рис. 20).
79

Но если при p>1 площадь под кривой конечна, то при
p 1 она бесконечна, т.к. в этом случае функции |
y |
1 |
|
|
|||
x p |
|||
|
|
убывают недостаточно быстро при x 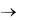 . Большинство свойств определѐнного интеграла (кроме оценки и теоремы о среднем) для несобственных интегралов сохраняются.
. Большинство свойств определѐнного интеграла (кроме оценки и теоремы о среднем) для несобственных интегралов сохраняются.
Если f(x) непрерывна на промежутке |
, a , то |
аналогично:
a a
f (x)dx |
lim |
f (x)dx . |
|
|
N |
|
|
|
|
N |
|
Если f(x) |
непрерывна |
на всей числовой оси, то |
|
(рис.21) |
|
|
|
|
a |
|
|
f (x)dx |
f (x)dx |
f (x)dx . |
|
a
y
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
хx |
|
a |
|
|
|
|||
|
|
|
|
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Рис. 21.
Интеграл, стоящий слева, называется сходящимся, если сходятся оба интеграла в правой части и расходящимся, если расходится хотя бы один из интегралов в правой части.
Часто бывает достаточно знать, сходится или расходится рассматриваемый несобственный интеграл.
80
