
2773
.pdf
Пример. |
Вычислить |
(1 |
|
|
i 10 . Запишем число |
z=1+i |
в |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
12 |
|
|
|
|
|
|
|
|
|||||||||||
тригонометрическом виде. Здесь |
r |
|
|
|
= 2 , |
|
||||||||||||||||||||||||||||||||||||||||||||
tg |
=1; |
|
|
|
|
|
|
|
|
|
; |
|
z = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 4). |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
cos |
|
|
|
|
i sin |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
4 |
4 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
i 10 |
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
|
2 |
cos 10 |
|
|
|
|
|
|
i sin 10 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||
|
|
25 cos |
5 |
|
|
|
|
i sin |
5 |
|
|
|
32 cos |
|
|
|
|
|
i sin |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
д) Извлечение корня. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Корнем n-ой степени из комплексного числа z |
||||||||||||||||||||||||||||||||||||||||||||||||||
называется такое число w (w= n |
|
), что |
wn=z. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
z |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Пусть числа z и w представлены в тригонометрической |
||||||||||||||||||||||||||||||||||||||||||||||||||
форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
z |
r cos |
|
|
|
|
i sin |
|
|
и w |
|
|
|
|
cos |
|
|
|
i sin . |
|
|
|
|
|||||||||||||||||||||||||||
Найдѐм ρ и . Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
wn |
z, |
n cosn |
|
|
i sin n |
|
|
r cos |
|
|
i sin |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
n |
r , n |
|
|
|
|
|
|
|
|
|
|
|
2 |
k |
k |
0, 1,... . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
ρ= n |
|
|
|
- |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Поэтому: |
|
r |
арифметическое |
|
значение |
корня |
из |
|||||||||||||||||||||||||||||||||||||||||||
положительного числа r, а |
= |
|
|
|
|
2k |
|
|
(k= 0, |
1, |
|
2,... ). Т.о. |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 k |
|
|
|
|
|
|
|
|
|
2 k |
|
|
|
|
|
|
|
|
|
|||||||||
|
wk |
n z |
|
n r |
|
cos |
|
|
i sin |
|
|
|
|
|
|
|
|
или |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
i |
|
|
|
2 k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n z |
n re |
|
|
|
n |
|
|
|
|
|
|
|
|
|
k |
|
0,1,2,..., n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Значение к, дающие существенно различные значения корня n-ой степени из z соответствуют только n значениям k (0,1,2,…n-1). Остальным целым k соответствуют значения k,
11

отличающиеся от одного из указанных значений на величину, кратную 2π.
Проверить, например, что wn=w0 !
Таким образом, комплексное число z 0 имеет ровно n корней степени n, получаемых из этих формул. Из формул вытекает, что все значения корня лежат на окружности
радиуса ρ= n r и делят окружность на n равных частей.
r и делят окружность на n равных частей.
Пример |
1: |
|
|
|
|
Вычислить |
|
|
|
|
3 |
|
|
|
. |
|
|
|
Запишем |
|
число |
в |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
тригонометрической форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
w0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
w1 |
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
i |
|
|
cos |
|
|
|
|
|
|
|
i sin |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 k |
|
|
|
|
|
2 k |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
w2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
cos |
|
|
|
3 |
|
|
|
|
|
|
i sin |
|
3 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
0,1,2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
Рис.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1. k |
0 W |
cos |
|
|
|
|
|
i sin |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
i |
; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
6 |
|
|
|
|
|
6 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2. k |
1 W |
|
|
cos |
|
5 |
|
|
|
|
i sin |
5 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
i |
|
; |
|
|
|
|
|
|
|||||||||||||||||||
6 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
3. k |
2 W |
cos |
3 |
|
|
i sin |
3 |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример |
2: |
|
|
|
|
Вычислить |
1 . |
|
|
|
Запишем |
число |
в |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
показательной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
1; |
|
|
|
|
|
; 1 |
1ei |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
2 k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
wk |
|
|
1 |
|
e |
|
|
k |
0,1,2,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
12

|
у |
w1 |
w0 |
|
х |
w2 |
w3 |
Рис. 6.
|
|
|
ei |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
; |
|
|
|
||
1. k |
0; W |
|
|
4 |
|
|
|
cos |
|
|
|
|
|
|
|
i sin |
|
|
|
|
|
|
|
|
|
i |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2. k 1; W ei |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
4 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
ei |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
3. k 2; W |
2 |
4 |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
ei |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
cos |
7 |
|
|
i sin |
7 |
|
|
|
2 |
|
|
|
|
2 |
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
4. k |
3; W |
|
|
|
4 |
|
|
|
|
|
|
|
|
i |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
4 |
|
|
4 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
13

2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2.1. Первообразная. Неопределѐнный интеграл
Основная задача дифференциального исчисления: по заданной функции ƒ(х) найти еѐ производную ƒ/(x) или дифференциал ƒ/(x)dx. Теперь будем решать обратную задачу: по заданной производной или дифференциалу найти саму функцию ƒ(х).
С точки зрения механики это значит, что по известной скорости движения найти закон движения.
Определение 1: функция F(x) называется первообразной функцией для функции ƒ(х) на интервале (a, b), если F(x) дифференцируема на (a, b) и F/(x)=ƒ(х) или dF(x)=ƒ(x)dx
x (a, b)
Простейшие примеры:
|
|
|
2 |
|
x3 |
|
|
1 |
|
|
3 |
1 |
|
2 |
|
|
1. f |
x |
x |
|
; F x |
|
, |
так как |
|
|
x |
|
|
3x |
|
; |
|
|
3 |
3 |
|
3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. f |
x |
cosx; F x |
sin x, |
так как |
|
sinx |
|
cosx |
||||||||
Если для ƒ(х) существует первообразная F(x), то существует и бесчисленное множество первообразных. Например, для ƒ(х) = х2 первообразными будут функции:
1 |
|
x |
3 |
; |
1 |
|
x |
3 |
1 |
; |
1 |
|
x |
3 |
20 |
и т.д. |
3 |
|
3 |
|
2 |
3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
Теорема 1: Если F(x) есть первообразная для функции ƒ(х) на (a, b), то функция F(х) + C – так же первообразная, где C - любое число.
Доказательство: так как F x |
f x , то |
F x c
c F
F x
x f x .
f x .
Даѐт ли формула F(x) + c все первообразные для ƒ(х) или могут быть какие-то другие, не содержащиеся в этой формуле?
14

Теорема 2: Если две функции F(x) и Ф(х) являются первообразными для ƒ(х) на (a,b), то их разность постоянна на этом интервале: Ф(х) – F(x) = C 
Доказательство: По условию Ф(х) = ƒ(x) и F/(x) = ƒ(х) x (a, b) , составим вспомогательную функцию φ(х) = Ф(х) –
F(x).
Очевидно: |
|
|
|
x |
Ф x F x |
Ф x F x f x f x 0 |
|
x |
a,b . |
|
|
Отсюда следует, что |
|
|
|
x c, т.е. Ф x F x c |
на (a, b) . |
||
Из данных теорем следует, что если F(x) есть первообразная для ƒ(х) на (a, b), то любая другая
первообразная Ф(х) для ƒ(х) на (a, b) имеет вид |
|
Ф x F x c . |
(1) |
Таким образом, если производные двух функций тождественно равны, то сами функции могут отличаться лишь на постоянное слагаемое.
Определение 2: Множество всех возможных первообразных функции ƒ(х) на интервале (a, b) называется неопределѐнным интегралом функции ƒ(х) и обозначается символом
f (
Знак  называется интегралом,
называется интегралом,
ƒ(х) – подынтегральная функция, ƒ(х)dx – подынтегральное выражение.
Таким образом, если F(x) – одна из первообразных для ƒ(х), то; по определению:
x)dx
y y=f(x,y)
x
0 |
b |
а |
Рис. 7.
15

f x dx F x c
c
Операцию нахождения неопределѐнного интеграла (первообразная) называют интегрированием функции ƒ(х). В приложениях интегрировать приходится чаще, чем дифференцировать.
Функция, имеющая первообразную, называется интегрируемой.
Теорема: Если функция ƒ(х) непрерывна на (a, b) то для неѐ существует первообразная на (a, b), т.е. она интегрируема.
2.2. Основные свойства неопределѐнного интеграла
Эти свойства вытекают непосредственно из определения. 1. Производная от неопределѐнного интеграла
равна подынтегральной функции (применяется для проверки):
f |
x dx |
f x |
так как, |
|
f |
x dx |
F x |
c F x |
f x |
2. Дифференциал от неопределѐнного интеграла равен подынтегральному выражению:
d f x dx  f x dx так как,
f x dx так как,
d f x dx d F x c
c dF x
dF x F
F x dx
x dx  f x dx
f x dx
3.dF(x)=F(x). Действительно:
dF(x)=  F/(x)dx=F(x)+C .
F/(x)dx=F(x)+C .
16

Tаким образом, символы ƒ и d, следующие за друг за другом в любой последовательности, взаимно уничтожаются (с точностью до С).
4. Постоянный множитель можно выносить за знак неопределѐнного интеграла:
|
Af x dx |
A |
f x dx . |
|
|
|
|
|
|
|
|
Действительно: |
|
|
|
|
|
|
Af x dx |
Af |
x и |
|
|
A f x dx |
A f x dx |
Af x . |
|||
5. Неопределѐнный интеграл от алгебраической суммы двух функций равен сумме неопределѐнных интегралов от слагаемых:
f x g x dx |
f x dx |
g x dx |
(верно для любого конечного числа слагаемых) f x g x dx
g x dx  f x
f x g x
g x и
и
f x dx g x dx |
f x dx |
g x dx |
f x g x
g x
2.3. Таблица неопределѐнных интегралов
Так как интегрирование есть операция обратная дифференцированию, то всякую формулу для производной конкретных функций можно обратить:
F x f x |
f x dx F x c |
17

Поэтому таблицу основных интегралов получаем из таблицы производных, записав, еѐ справа налево:
1. |
xadx |
|
xa |
1 |
|
c |
a |
|
|
1 |
|
|
||||||||||||||
|
a |
1 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2. |
|
dx |
ln |
|
x |
|
|
|
|
c |
x |
0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
a x |
|
|
|
|
|
|
|
|
|
|||||||||
3. |
a xdx |
|
|
c |
a |
0; a |
1 |
|||||||||||||||||||
|
ln a |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4. |
|
exdx ex |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|||||||||||
5. |
sin xdx |
|
|
|
|
|
|
cos x |
c |
|
|
|
|
|
|
|||||||||||
6. |
cos xdx |
|
|
|
sin x |
c |
|
|
|
|
|
|
||||||||||||||
7. |
|
|
|
dx |
|
|
tgx |
c |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
cos2 x |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
8. |
|
|
|
dx |
|
|
|
|
ctgx |
c |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
sin2 x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
9. |
|
|
|
|
dx |
|
|
|
|
|
|
|
arcsin x |
|
c |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arccosx |
|
c |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arcsin |
x |
|
|
|
c |
||
10. |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||
|
|
|
|
|
a2 |
|
|
x2 |
|
|
|
|
|
|
arccos |
c |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|||||
11. |
|
|
|
|
|
dx |
|
|
|
|
|
|
arctgx |
c |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x2 |
|
|
|
|
|
|
|
|
arcctgx |
c |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
18

|
|
|
|
|
|
|
|
|
|
|
1 |
|
arctg |
x |
|
|
c |
|
|
||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
||||||||||||
12. |
|
|
|
|
|
|
a |
a |
|
|
|
|
|||||||||||||
|
|
a2 |
x2 |
1 |
|
arcctg |
x |
c |
|||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a |
|
||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
13. |
|
|
|
|
|
|
ln |
x |
x2 |
|
a2 |
c |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x2 |
a2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
dx |
|
|
|
|
|
1 |
a |
x |
|
|
|
|
|
||||||||
14. |
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
c |
|
|
||||||||
|
|
a2 |
x2 |
|
2a |
a |
x |
|
|
|
|||||||||||||||
Все эти формулы проверяются дифференцированием правой части.
1) Проверим формулу 3, т.е. докажем, что (ln|x|)′= |
1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
x |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а) x > 0, тогда | x | |
|
|
x и |
|
|
(ln | x |) |
|
(lnx) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b)x<0, тогда | x | |
-x и |
(ln | x |) |
|
ln x |
|
|
1 |
|
|
x |
1 |
,т.е. |
|||||||||||||||||||||||||||||||||||
|
|
x |
|
|
x |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ln | x | |
1 |
. Вообще: |
ln | u | |
1 |
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2) |
Проверим формулу 10: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
arcsin |
x |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
a |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a |
1 |
|
|
|
x 2 a |
a 2 |
x 2 a |
|
|
|
a 2 |
x 2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) |
Проверим формулу 12: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1 |
arctg |
x |
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
a |
|
|
|
|
|
a |
1 |
|
|
x 2 a x 2 |
a 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4) |
Проверим формулу 13: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
19
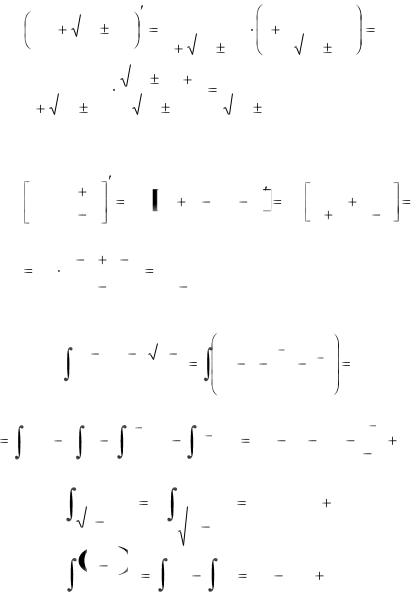
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|||||
|
|
ln |
|
x |
|
|
|
|
x2 |
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
a2 |
x2 |
a2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x2 |
|
a2 |
x |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x2 |
|
a2 |
|
|
|
|
|
|
x2 a2 |
|
|
|
|
|
|
|
x2 |
a2 |
|
|
|
|
|
|
|
||||||||||||||||
5) |
|
Проверим формулу 14: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1 |
|
|
|
|
a x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
ln |
|
|
|
|
|
|
|
|
ln |
a x |
|
ln |
a x |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2a |
a x |
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a a x a x |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
1 |
|
|
a |
|
x |
|
a |
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2a |
|
|
|
a2 |
|
x2 |
|
|
|
|
|
|
a2 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Примеры: Вычислить неопределенные интегралы.
|
x4 |
|
2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x x |
1 |
|
|
|
|
x2 |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1. |
|
|
|
|
2 x 2 x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
1 |
|
|||||||||
x2dx 2 dx |
|
|
|
|
|
|
|
|
|
|
x 2dx |
|
|
x 2 |
|
x |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
2 dx |
|
|
|||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
c |
||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
1 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
2. |
|
|
|
dx |
|
|
|
|
1 |
|
|
|
|
dx |
|
|
|
|
|
|
1 |
arcsin2x |
|
|
c |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||
1 |
|
4x |
2 |
|
|
|
|
|
|
1 |
|
x |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
1 dx |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
ln |
x |
|
|
c |
|
|
|
|
||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Интегралы, содержащиеся в таблице, называются табличными и их надо твѐрдо запомнить, т.к. вычисление интеграла сводится к последовательным операциям,
20
