2773

Из области определения функции следует, что

Построенная кривая носит название лемнискаты Бернулли. Ее вид представлен на рисунке 40.

3. Площадь в полярных координатах.

площадь криволинейного сектора, ограниченного данной линией и двумя лучами: и , выходящими из полюса.

Возьмѐм произвольное значение 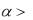и увеличим угол на бесконечно малую величину d . Тогда к площади добавится бесконечно малый криволинейный

полярных координатах.

101

Пример 2. Найти площадь, ограниченную линией :

=а sin 6 (а>0) (шестилепестковая роза).

Внашем случае достаточно вычислить площадь одного

102

4.4. Дифференциал длины дуги плоской кривой. Вычисление длин дуг

Пусть дана функция f(x) имеющая непрерывную производную на отрезке a, b . Геометрически это означает,

что на кривой АВ нет ни угловых точек, ни точек возврата. Такие линии называются гладкими.

N B

y

M

P

A

L L(x) . Найдѐм дифференциал этой функции.

Оказывается, для этого нет необходимости знать аналитическое выражение для L(x). Для этого достаточно

103

Если x 0 , то L и MN - бесконечно малые величины. Можно доказать, что длина бесконечно малой гладкой дуги и стягивающей еѐ хорды являются эквивалентными бесконечно малыми величинами:

длина соответствующего отрезка касательной к кривой в точке М. Пусть кривая АВ задана параметрически:

Это дифференциал длины дуги параметрически заданной кривой.

Если гладкая кривая задана в декартовых координатах: y=f(x), то из (9):

104

a

Если кривая задана параметрически, то из (I0):

t0

Пример. Найти длину дуги астроиды:

y

а ( /2)

-а

Рис. 43.

В силу симметрии фигуры, вычислим длину дуги,

расположенную в первой четверти т.е. 14 L .

Найдем производные:

105

4.5. Площадь поверхности вращения

Пусть непрерывная кривая y f (x) 0 , заданная на отрезке a, b , вращается вокруг оси Ох. Найдѐм площадь поверхности вращения.

y dL

x+dx в

Рис. 44.

В точке с абсциссой х проведѐм плоскость, перпендикулярную оси Ох. Она пересечѐт поверхность по окружности радиуса y=f(x). Через бесконечно близкую точку x dx проведѐм другую плоскость, перпендикулярную первой. Эти плоскости выделят бесконечно узкую полоску поверхности, площадь

106

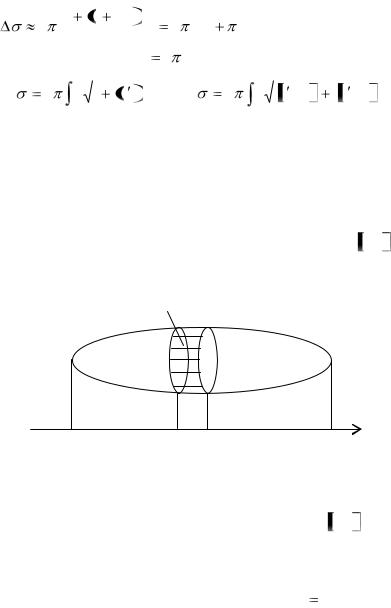
которой можно вычислить по формуле для усечѐнного конуса:

высшего порядка. d 2 ydL .

4.6. Вычисление объѐма тела по известным площадям поперечных сечений.

Объѐм тела вращения

1. Пусть дано тело, ограниченное замкнутой поверхностью, которое проектируется на отрезок a, b оси

Ох. В произвольной точке х проведѐм плоскость, перпендикулярную оси Ох.

dx

S(x)

Величина площади поперечного сечения будет зависеть от х: S=S(x). Предположим, что эта зависимость известна, причѐм S(x) непрерывна на a, b . Через

бесконечно близкую точку проведѐм другую плоскость, параллельную первой. Тогда из объѐма будет выделен бесконечно малый слой dV, который можно принять за цилиндр с основанием S(x) и высотой dx: dV S(x)dx и

107

b

a

Пример. Найти объѐм пирамиды с основанием В и высотой Н.

O

S(x)

x H

B

х

Ох. Найдѐм объѐм тела вращения. Это – частный случай предыдущей задачи. Любое сечение данного тела плоскостью, перпендикулярной оси Ох, есть круг радиуса R y f (x) .

108

dx

Рис. 47

Отсюда:

прямой х=1, вращается вокруг оси Ох. Найти объѐм тела вращения.

109

4.7. Статические моменты и координаты центра масс плоской фигуры

Статическим моментом материальной точки относительно оси ol называется произведение массы этой точки на еѐ расстояние до оси:

Ke mr

Если в плоскости Оху дана система материальных точек, то статическим моментом системы относительно координатной оси называется сумма статических моментов всех точек системы относительно этой оси:

относительно любой оси равен статическому моменту системы точек относительно той же оси:

Пусть y=f(x) непрерывна на a, b . На криволинейной трапеции распределена масса с поверхностной плотностью const . Выделим бесконечно узкий элемент фигуры с

основанием dx и высотой f(x) (который можно считать прямоугольником). Его масса будет:

110