
2773
.pdf
результатом которых являются приведения заданного интеграла к табличному (если это возможно).
2.4. Интегрирование с помощью замены переменной
Одним из самых сильных методов интегрирование является метод замены переменной.
Пусть надо вычислить интеграл |
|
F(x)dx. |
(2) |
Часто его можно упростить, введя вместо х новую |
|
переменную t, положив |
|
x = φ(t) и dx = φ′(t)dt . |
(3) |
Для преобразования неопределѐнного интеграла (2) к новой переменной t по формуле (3) достаточно преобразовать к новой переменной его подынтегральное выражение:
f x dx |
f t |
t dt |
(4) |
В формуле (4) предполагается, что ƒ(х) непрерывна на некотором промежутке оси Ох, а функции φ(t) и φ′(t) непрерывны на соответствующем промежутке изменения t. Это равенство надо понимать так: после интегрирования левой части по х и подстановки х = φ(t) мы должны получить тождество.
Для доказательства формулы (4) вычислим дифференциал от обеих частей:
d |
f |
x d x |
|
x |
t |
f x d x |
|
x |
t |
f t |
t dt и |
|
|
|
|
|
|
||||||
d |
f |
t |
t dt |
f t |
t dt . |
|
|
||||
21

Раз дифференциалы двух функций тождественно равны, то сами функции отличаются на постоянное слагаемое С. В этом смысле и надо понимать (4).
Замечание 1: Часто вместо подстановки (4) употребляют обратную:
|
x t ; |
x dx |
dt . |
|
(5) |
|
|
Замечание 2: Так как |
|
|
|||
|
|
f |
t |
t dt |
f |
t d t , |
то, |
если |
f (x)dx |
F x |
c , |
|
|
из |
(4) следует: |
f |
t |
d t |
F t |
c |
Таким образом, вид неопределѐнного интеграла не зависит от выбора аргумента интегрирования. Этот факт используется при интегрировании способом подведением под знак дифференциала.
Примеры:
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
1 |
|
|||
1. |
x dx |
|
|
c |
|
|
sin x |
d sin x |
|
|
|
|
c |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
u |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
u |
du |
|
|
|
|
|
c u |
|
sin x |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
sin xdx |
|
cos x |
c |
|
|
sin ex dex |
|
|
|
|
cos ex |
|
c . |
||||||||||
3. 2xe x2 dx |
|
|
e x2 d x2 |
e x2 |
|
|
c |
u |
x2 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
sin x 2 d sin x |
|
|
|
|||||||||||||
4. |
|
sin x cos xdx |
|
c u |
|
cos x . |
||||||||||||||||||
|
|
|
3 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
22

5. |
|
tgxdx |
sin xdx |
|
|
d cosx |
ln |
|
cos x |
|
c |
|||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
cos x |
|
|
cosx |
|||||||||||||||
Вообще: |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
f |
x |
|
df |
x |
|
|
|
|
|
|
|
|
||||
|
|
dx |
ln |
f x |
c |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
f |
x |
f |
x |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если в числе стоит производная знаменателя, то интеграл от дроби равен логарифму от модуля знаменателя.
|
|
|
|
|
|
|
|
x |
|
5 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. |
x x |
|
|
5dx |
x |
|
5 |
|
|
|
|
5 t2tdt |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
2tdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2t4 |
10t2 dt |
|
t |
5 |
|
|
|
t |
3 |
|
|
|
|
2 |
|
|
|
5 |
10 |
|
3 |
|
||||||||||
|
|
2 |
|
|
10 |
|
|
c |
x 5 |
|
|
x 5 |
|
|
c |
|||||||||||||||||||
|
|
|
|
2 |
2 |
|||||||||||||||||||||||||||||
|
5 |
|
|
|
5 |
|
|
3 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
xdx |
|
|
x2 |
1 |
|
t |
|
1 |
|
|
dt |
|
|
1 |
|
|
|
|
1 |
ln x2 |
|
|
||||||||||
7. |
|
|
|
|
|
ln |
t |
|
c |
1 |
c |
|||||||||||||||||||||||
|
x2 |
1 |
|
2dx |
dt |
2 |
|
|
t |
2 |
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2.5. Правило интегрирования по частям
Пусть функции u = u(x) и v = v(x) имеют непрерывные производные. Тогда по правилу дифференцирования произведения имеем:
d uv vdu udv
Интегрируем обе части равенства по х:
d uv |
vdu udv uv |
vdu |
udv |
|
udv uv |
vdu . |
|
(7) |
|
|
|
|
|
|
23

Эта формула называется формулой интегрирования по
частям. Формула сводит |
вычисление интеграла |
udv к |
вычислению интеграла |
vdu, который может |
оказаться |
проще исходного. При этом за u(x) обычно выбирают множитель подынтегрального выражения, который при дифференцировании упрощается, а за dv – множитель, который нетрудно проинтегрировать.
Пример 1: Вычислить неопределенные интегралы, используя метод интегрирования по частям.
. xexdx |
|
|
u |
x |
du |
|
|
dx |
|
|
|
|
|
|||
|
dv |
exdx v |
|
ex |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
xex |
exdx xex |
ex |
c. |
|
|
|
|
|
|||||||
Пример 2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x cos xdx |
u |
x |
|
du |
dx |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
dv |
cos xdx |
|
v sin x |
|
|
||||||
|
x sin x |
|
sin xdx |
x sin x |
|
cos x |
|
c. |
|
|
||||||
Пример 3: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
u |
ln x, du |
dx |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
x6 |
|
x6 |
|
||||
x5ln xdx |
x |
|
ln x |
dx |
||||||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
x6 |
|
6 |
|
6 |
|
|||
|
|
u |
|
|
dv |
x5dx, v |
|
|
|
|||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x6 |
|
x6 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ln x |
|
|
c . |
|
|
|
|
|
|
|
|
|
|
|
6 |
36 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
24

Интегрирование по частям приводит к успеху при интегрировании выражений вида:
eax P x dx , |
P |
x sin xdx; |
P |
|
x cos xdx; |
P |
x ln xdx. |
|||||
|
n |
|
n |
|
|
n |
|
|
n |
|
||
Пример 4: |
|
|
|
|
|
|
|
|
|
|||
. (x2 |
2x 3)exdx |
u x2 |
|
2x 3 du (2x 2)dx |
||||||||
|
|
|
|
|
dv |
|
exdx |
|
v |
ex |
||
|
(x2 |
2x 3)ex |
(2x 2)exdx |
|
|
|
||||||
Применим ко второму интегралу еще раз формулу |
||||||||||||
интегрирования по частям |
|
|
|
|
|
|
||||||
. |
u |
2x |
2 |
du |
2dx |
(x2 2x 3)ex |
(2x 2)ex |
|||||
dv |
exdx |
v |
ex |
|||||||||
|
|
|
|
|
|
|
||||||
|
2 exdx (x2 |
2x 3)ex |
(2x 2)ex 2ex |
c. |
||||||||
Пример 5*: |
|
|
|
|
|
|
|
|
|
|||
|
ex sin xdx |
|
u ex , du |
exdx |
ex cos x |
|||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
dv |
sin xdx, v |
|
cos x |
|
|
|
||
|
ex cos xdx |
u |
ex , du |
|
exdx |
ex cos x |
ex sin x |
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
v |
cos x |
|
|
|
|
|
|
|
ex sin xdx.
Получили интеграл равный данному. Обозначив его за J, получим равенство
J e x sin x cos x J .
J .
Перенося J в левую часть равенства, имеем
25
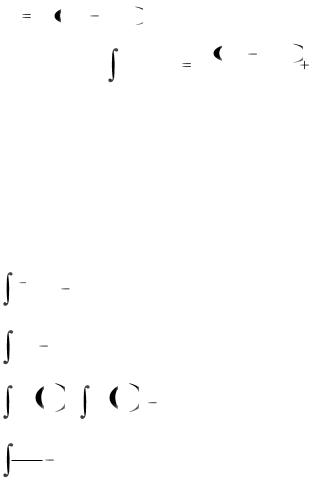
2J e x sin x |
cos x . |
|
|
|
Окончательно: |
ex sin xdx |
ex sin x |
cos x |
c |
|
|
|||
2 |
|
|||
|
|
|
|
2.6. Об интегрировании в элементарных функциях
Операция дифференцирования элементарной функции снова приводит к элементарным функциям. Интегрирование элементарной функции часто приводит к неэлементарным функциям, т.е. функциям задаваемых одной формулой, содержащей конечное число операций. Например, доказано, что такими являются интегралы:
e x2 dx интеграл Пуассона,
dx |
интегральный логарифм, |
|
|
||
ln x |
||
|
cos x2 dx, sin x2 dx интегралы Френеля, |
||
sin x |
интегральный синус и т.д. |
|
x |
||
|
||
Первообразные для этих функций существуют, но не выражаются через элементарные функции. Наиболее важные из этих первообразных протабулированы.
В связи со сказанным, полезно рассмотреть классы функций, первообразные которых являются элементарными функциями.
26

2.7. Многочлен степени n. Теорема Безу. Условие тождественности двух многочленов
Рассмотрим многочлен степени n:
P x a |
a x |
a |
2 |
x2 |
... a |
n |
xn |
a |
n |
0 |
(8) |
n |
0 1 |
|
|
|
|
|
|
|
Здесь как коэффициенты, так и значения переменной х могут быть как действительными так и комплексными.
Каждое действительное или комплексное значение х0, которое обращает Pn (x) в нуль, называется корнем этого многочлена:
Pn x0  0.
0.
Следовательно, корни многочлена (8) представляют собой решения алгебраического уравнения n – ой степени:
Pn x 0.
0.
Формула Тейлора применима как для действительных многочленов, так и для многочлена (8):
Pn |
x |
Pn |
x0 |
|
Pn x0 |
x x0 |
Pn x0 |
x x0 2 ... |
|||
1! |
2! |
||||||||||
|
|
|
|
|
|
|
(9) |
||||
|
|
n |
|
|
|
|
|
|
|
||
|
P |
x |
0 |
|
x0 n |
|
|
|
|||
|
n |
|
x |
|
|
|
|||||
|
|
n! |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
Отсюда следует, что для того, |
чтобы точка х = х0 была |
||||||||||
корнем многочлена Pn (x), необходимо и достаточно, чтобы
свободный член разложения многочлена по степеням (х - х0) был равен нулю:
Pn x |
Pn |
|
x0 |
x |
x0 |
Pn x0 |
x x0 2 ... |
||
|
|
1! |
2! |
||||||
|
|
|
|
|
|
|
|||
|
P n |
x |
0 |
|
|
|
n |
|
|
|
n |
|
|
x |
x0 |
|
|
||
|
n! |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
В этом случае многочлен можно представить в виде:
27

Pn x |
x |
|
x0 [Pn |
x0 |
Pn |
x0 |
x |
x0 2 ... |
|||
|
2! |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
n x |
0 |
|
|
x0 n 1 ] |
|
|
|
|
|
|
n |
|
|
x |
|
|
|
|
|||
|
|
n! |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
или |
Pn |
x |
|
x |
x0 Pn 1 x |
|
|
(10) |
|||
Наоборот, |
если |
Pn (x) из (8) можно представить в виде |
|||||||||
(10), т.е. |
Pn (x) |
можно разделить на (х |
х0) без остатка, то |
||||||||
очевидно, |
что |
х = |
х0 |
есть |
корень |
Pn (x). Таким образом, |
|||||
доказана теорема: |
|
|
|
|
|
|
|||||
Теорема |
Безу: |
Для |
того, |
чтобы |
многочлен Pn (x) имел |
||||||
корень х = х0, необходимо и достаточно, чтобы он делился на
(х х0), т.е. был представим в виде (10). |
|
|
||||
Если |
P (x) = 0, а P / |
(x) 0 то корень х = х0 называется |
||||
|
n |
n |
|
|
|
|
простым. |
|
|
|
|
|
|
В этом случае в формуле (10) |
Pn 1 (x0) |
0 |
и, согласно |
|||
теореме Безу, его нельзя разделить на х – х0. |
|
|
||||
Если |
P (x0) = |
P /(x0) = … = |
Pk 1 (x0) |
= 0, |
Pk (x0) 0 |
|
|
n |
n |
|
n |
|
n |
k n , то х = х0 называется корнем кратности k.
Тогда формула Тейлора для Pn (x) по степеням х – х0 имеет вид:
|
|
|
P |
k |
x x0 k |
P |
k 1 |
k 1 ... |
||||
Pn x |
|
|
n |
|
n |
|
x x0 |
|||||
|
|
k! |
k |
1 ! |
||||||||
|
|
|
|
|
|
|
|
|||||
|
P |
n x |
0 |
|
|
|
n . |
|
|
|
|
|
|
n |
|
|
x |
x0 |
|
|
|
|
|||
|
|
n! |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
28

|
|
|
|
|
|
|
|
|
k |
|
P |
k |
x |
0 |
|
|
P k |
1 |
x |
0 |
|
|
|
||
|
|
Pn x |
x x0 |
|
|
n |
|
|
|
|
|
n |
|
|
x x0 ... |
|
|||||||||
|
|
|
|
|
|
k! |
|
|
|
k |
|
1 ! |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
P n |
x |
0 |
|
|
|
|
|
n |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
x |
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
P |
|
x |
x |
x |
0 |
k |
P |
|
k |
x , |
|
где |
P |
|
|
0 |
|
(11) |
|||||
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n-k |
|
|
|
|
||||
|
Если х= х0 |
есть корень многочлена Pn (x) кратности k, то |
|||||||||||||||||||||||
многочлен делится на (х |
|
х0)k. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Если значения двух многочленов совпадают для всех х |
||||||||||||||||||||||||
Pn |
x |
|
Qn |
x , |
то |
|
эти |
многочлены |
имеют |
одинаковые |
|||||||||||||||
коэффициенты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Действительно, |
|
|
из |
|
|
|
(9) |
|
следует, |
что |
если |
|||||||||||||
Pn |
x |
|
Qn |
x |
|
F ( x) |
, |
то коэффициенты обоих многочленов |
|||||||||||||||||
будут вычисляться по одним и тем же формулам:
A0 |
f 0 ; Ak |
f k |
0 |
k 1,2,...n |
k! |
|
|||
|
|
|
|
2. 8. Основная теорема алгебры. Разложение многочлена с действительными коэффициентами на
линейные и квадратные многочлены
Теорема: Всякий многочлен степени n 1 имеет, по крайней мере, один действительный комплексный корень.
Замечание: То, что в теореме говорится о многочлене, существенно. Неалгебраическое уравнение может не иметь ни
действительных, ни комплексных корней. Например: |
ех = 0. |
|||||||
Действительно, при любом комплексном х = α +iβ |
||||||||
e x e i |
e ei |
e cos |
i sin |
|
e x |
|
e |
0 . |
|
|
|||||||
29

Следствие: Многочлен Pn (x) степени n имеет n корней с учѐтом их кратности, т.е. представим в виде произведения:
P x |
a |
n |
x |
x |
r1 x x |
r2 ... x |
x |
rm , |
(12) |
n |
|
|
1 |
|
2 |
|
m |
|
|
где x1, x2, …xm |
– различные корни многочлена |
Pn (x) |
|||||||
кратности r1, r2, …rm |
(r1+r2+…+rm |
n). Некоторые (или все) |
|||||||
корни могут быть комплексными. |
|
|
|
||||||
Доказательство:
По основной теореме многочлен имеет хотя бы один корень. Обозначим его через х, а его кратность через r1. Тогда по формуле (11):
P x |
x x r1 |
P |
r |
x , P |
|
x |
0 |
|
|
|
n |
1 |
n |
n r |
1 |
|
|
|
|
||
|
|
|
1 |
|
1 |
|
|
|
|
|
Если r1 |
= n, то |
Pn |
k |
x an |
|
и Pn (x)=(х-х1)nan |
и теорема |
|||
|
|
|
1 |
|
|
|
|
|
|
|
доказана. |
|
|
|
|
|
|
|
|
|
|
Если r1<n и к многочлену степени n – r1, |
Pn k |
x |
снова |
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
применяем основную теорему. Обозначим корень этого многочлена через х2, а его кратность через r2. В результате получим:
P x |
x x |
r1 |
x x |
r2 |
P |
|
r |
|
x , P |
|
|
x |
2 |
0. |
n |
|
1 |
|
2 |
n r |
2 |
n r r |
2 |
|
|
||||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
||
Процесс закончится через конечное число шагов (не большего n) и мы придем к формуле (12).
Если в правую часть (12) подставить вместо х число, отличное от x1, x2, …xm , то она не обратится в нуль. Это показывает, что других корней, кроме найденных, многочлен Pn(x) не имеет и представление (12) единственно.
Все сказанное до сих пор относится к многочленам как с действительными, так и с комплексными коэффициентами. Пусть теперь многочлен Pn(x) имеет действительные коэффициенты и пусть у него имеется комплексный корень кратности s:
xk = α + iβ.
30
